Αρχείο:Binary decomposition.png

Εικόνα σε υψηλότερη ανάλυση (2.000 × 2.000 εικονοστοιχεία, μέγεθος αρχείου: 49 KB, τύπος MIME: image/png)
| Αυτό το αρχείο και η περιγραφή του προέρχονται από το Wikimedia Commons. Οι πληροφορίες από την σελίδα περιγραφής του εκεί εμφανίζονται παρακάτω. |
Περιεχόμενα
Σύνοψη
| ΠεριγραφήBinary decomposition.png |
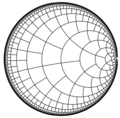
English: Binary decomposition of unrolled circle plane. Relation between binary decomposition and binary numbers. It is a graphical explanation how to convert proper decimal fraction to binary fraction. A decomposition of a Carleson square into dyadic Whitney boxes |
| Ημερομηνία | |
| Πηγή | Έργο αυτού που το ανεβάζει |
| Δημιουργός | Adam majewski |
| άλλες εκδόσεις |
|
Αδειοδότηση
- Είστε ελεύθερος:
- να μοιραστείτε – να αντιγράψετε, διανέμετε και να μεταδώσετε το έργο
- να διασκευάσετε – να τροποποιήσετε το έργο
- Υπό τις ακόλουθες προϋποθέσεις:
- αναφορά προέλευσης – Θα πρέπει να κάνετε κατάλληλη αναφορά, να παρέχετε σύνδεσμο για την άδεια και να επισημάνετε εάν έγιναν αλλαγές. Μπορείτε να το κάνετε με οποιοδήποτε αιτιολογήσιμο λόγο, χωρίς όμως να εννοείται με οποιονδήποτε τρόπο ότι εγκρίνουν εσάς ή τη χρήση του έργου από εσάς.
- παρόμοια διανομή – Εάν αλλάξετε, τροποποιήσετε ή δημιουργήσετε πάνω στο έργο αυτό, μπορείτε να διανείμετε αυτό που θα προκύψει μόνο υπό τους όρους της ίδιας ή συμβατής άδειας με το πρωτότυπο.
Σύνοψη
Relation between binary decomposition and external angles for quadratic polynomials[1]

-
circle plane
-
unrolled circle plane
There are 3 planes :
- extended complex plane ( parameter eplane or dynamic plane, but dynamic is easier to understand), for example plane for fc(z) = z*z +c where c= -2
- extended complex plane for c= 0
- above plane where circle is transformed int streight segment ( from 0 to 1 ). It can be called unrolled circle plane
Lines :
- horizontal are boundaries of escape time level sets ( dwell bands )
- vertical are dynamic external rays
Note that distance between horizontal lines is getting smaller when trace from up to down. Light gray band at the bottom of the image is a Juli a set.
how to convert proper decimal fraction to binary fraction
When fraction :
- is greater then 1/2 then it starts with 0.1
- is smaller then 1/2 then it starts with 0.0
( to do )
So when I trace external ray ( vertical line ) :
- inwards ( from point at infinity towards Julia set ) I add bit at the end each time I cross level set boundary ( horizontal line )
- outwards ( from boundary of Julia set toward point at inifinity) I add the bit at the beginning
C src code
"an image is basically a matrix" so program uses 2 arrays ( edge and data).
Program checks every pixel of the image ( see FillArray function ) :
// for all pixels of image
for(iy = iyMin; iy<=iyMax; ++iy)
{ printf(" %d z %d\n", iy, iyMax); //info
for(ix= ixMin; ix<=ixMax; ++ix) PlotPoint(A, ix, iy, IterationMax, iMethod ) ; //
}
converts from c=0 plane to unrolled circle plane converting :
- horizontal coordinate x to argument of complex number z
- vertical coordinate y to radius of complex number z
It can be done using GiveZ function :
// from screen to world coordinate mapping
complex double GiveZ(unsigned int ix, unsigned int iy)
{
double Zx, Zy; // Z=Zx+Zy*I = radius*e^{turn*2*pi*I}
double turn = ((double) ix)/((double ) ixMax); // arg(Z)
double radius = ((double) (iyMax-iy))/((double) iyMax); // abs(Z)
Zx = ZxMax*radius*cos(turn*2.0*pi);
Zy = ZyMax*radius*sin(turn*2.0*pi);
return (Zx+ I*Zy);
}
and computes it's color ( see ComputeColor function) :
- if point escapes then it is exterior of the Julia set
- if point do not escapes then it is interior of the Julia set
if (Zx2+Zy2<1.0) return iColorOfInterior;
if (Zx2+Zy2>ER2)
{ switch( iMethod )
{
case 1: // level set method
if (i%2 == 0) return 150;
else return 190;
break;
case 2: // binary decomposition method
if (Zy>0) return iColorOfExteriorUp;
else return iColorOfExteriorDown;
break;
} // switch
}
Exterior can be colored using 2 methods :
Program creates 6 pgm images.
/*
Adam Majewski
adammaj1 aaattt o2 dot pl // o like oxygen not 0 like zero
fraktal.republika.pl
c console progam
How to compute iteration :
gcc r.c -lm -Wall -march=native
time ./a.out
m
*/
#include <stdio.h>
#include <stdlib.h> // malloc
#include <string.h> // strcat
#include <math.h> // M_PI; needs -lm also
#include <complex.h>
/* --------------------------------- global variables and consts ------------------------------------------------------------ */
// virtual 2D array and integer ( screen) coordinate
// Indexes of array starts from 0 not 1
//unsigned int ix, iy; // var
static unsigned int ixMin = 0; // Indexes of array starts from 0 not 1
static unsigned int ixMax ; //
static unsigned int iWidth ; // horizontal dimension of array
static unsigned int iyMin = 0; // Indexes of array starts from 0 not 1
static unsigned int iyMax ; //
static unsigned int iHeight = 2000; //
// The size of array has to be a positive constant integer
static unsigned int iSize ; // = iWidth*iHeight;
// memmory 1D array
unsigned char *data;
unsigned char *edge;
unsigned char *edge1;
// unsigned int i; // var = index of 1D array
//static unsigned int iMin = 0; // Indexes of array starts from 0 not 1
static unsigned int iMax ; // = i2Dsize-1 =
// The size of array has to be a positive constant integer
// unsigned int i1Dsize ; // = i2Dsize = (iMax -iMin + 1) = ; 1D array with the same size as 2D array
/* world ( double) coordinate = dynamic plane */
static const double ZxMin=-10.0;
static const double ZxMax=10.0;
static const double ZyMin=-10.0;
static const double ZyMax=10.0;
static double PixelWidth; // =(ZxMax-ZxMin)/ixMax;
static double PixelHeight; // =(ZyMax-ZyMin)/iyMax;
static double ratio ;
static unsigned long int iterMax = 1000; //iHeight*100;
static double ER = 9.0; // Escape Radius for bailout test
static double ER2;
/* colors = shades of gray from 0 to 255 */
// 8 bit color = int number from 0 to 255
unsigned char iColorOfInterior=200; //
static unsigned char iColorOfExteriorUp = 125;
static unsigned char iColorOfExteriorDown = 245;
static unsigned char iColorOfUnknown = 100;
long int iUknownPixels=0;
const double pi = 3.141592653589793;
/* ------------------------------------------ functions -------------------------------------------------------------*/
//------------------complex numbers -----------------------------------------------------
// from screen to world coordinate mapping
// uses global cons
complex double GiveZ(unsigned int ix, unsigned int iy)
{
double Zx, Zy; // Z=Zx+Zy*I = radius*e^{turn*2*pi*I}
double turn = ((double) ix)/((double ) ixMax); // arg(Z)
double radius = ((double) (iyMax-iy))/((double) iyMax); // abs(Z)
Zx = ZxMax*radius*cos(turn*2.0*pi);
Zy = ZyMax*radius*sin(turn*2.0*pi);
return (Zx+ I*Zy);
}
// uses globaal cons
//double GiveZy(unsigned int ix, unsigned int iy)
// { return (ZyMax - iy*PixelHeight);} // reverse y axis
/* ----------- array functions = drawing -------------- */
/* gives position of 2D point (ix,iy) in 1D array ; uses also global variable iWidth */
unsigned int Give_i(unsigned int ix, unsigned int iy)
{ return ix + iy*iWidth; }
// plots raster point (ix,iy)
int iDrawPoint(unsigned char A[], unsigned int ix, unsigned int iy, unsigned char iColor)
{
/* i = Give_i(ix,iy) compute index of 1D array from indices of 2D array */
A[Give_i(ix,iy)] = iColor;
return 0;
}
//;;;;;;;;;;;;;;;;;;;;;; setup ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
int setup()
{
printf("setup\n");
/* 2D array ranges */
iWidth = iHeight;
iSize = iWidth*iHeight; // size = number of points in array
// iy
iyMax = iHeight - 1 ; // Indexes of array starts from 0 not 1 so the highest elements of an array is = array_name[size-1].
//ix
ixMax = iWidth - 1;
/* 1D array ranges */
// i1Dsize = i2Dsize; // 1D array with the same size as 2D array
iMax = iSize-1; // Indexes of array starts from 0 not 1 so the highest elements of an array is = array_name[size-1].
/* Pixel sizes */
PixelWidth = (ZxMax-ZxMin)/ixMax; // ixMax = (iWidth-1) step between pixels in world coordinate
PixelHeight = (ZyMax-ZyMin)/iyMax;
ratio = ((ZxMax-ZxMin)/(ZyMax-ZyMin))/((float)iWidth/(float)iHeight); // it should be 1.000 ...
// for numerical optimisation in iteration
ER2 = ER * ER;
/* create dynamic 1D arrays for colors ( shades of gray ) */
data = malloc( iSize * sizeof(unsigned char) );
edge = malloc( iSize * sizeof(unsigned char) );
edge1 = malloc( iSize * sizeof(unsigned char) );
if (edge1==NULL || edge== NULL || data == NULL)
{
fprintf(stderr," Could not allocate memory");
getchar();
return 1;
}
printf(" end of setup \n");
return 0;
} // ;;;;;;;;;;;;;;;;;;;;;;;;; end of the setup ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
unsigned char ComputeColor(unsigned int ix, unsigned int iy, int IterationMax, int iMethod)
{
// check behavour of z under fc(z)=z^2+c
// using 2 target set:
// 1. exterior or circle (center at origin and radius ER )
// as a target set containing infinity = for escaping points ( bailout test)
// for points of exterior of julia set
// 2. interior of circle with center = alfa and radius dMaxDistance2fixed
// as a target set for points of interior of Julia set
// Z= Zx+ZY*i;
int i=0; // number of iteration
complex double Z; // Z= Zx + Zy*I
double Zx, Zy;
double Zx2, Zy2; // Zx2 = Zx* Zx
// from screen to world coordinate
Z = GiveZ(ix,iy);
Zx = creal(Z);
Zy = cimag(Z);
//
Zx2=Zx*Zx;
Zy2=Zy*Zy;
if (Zx2+Zy2<1.0) return iColorOfInterior;
if (Zx2+Zy2>ER2)
{ switch( iMethod )
{
case 1: // level set method
if (i%2 == 0) return 150;
else return 190;
break;
case 2: // binary decomposition method
if (Zy>0) return iColorOfExteriorUp;
else return iColorOfExteriorDown;
break;
} // switch
}
// if not inside target set around
while (i< IterationMax)
{ // then iterate
Zy=2*Zx*Zy ;
Zx=Zx2-Zy2 ;
Zx2=Zx*Zx;
Zy2=Zy*Zy;
// escaping test
if (Zx2+Zy2>ER2)
{ switch( iMethod )
{
case 1: // level set method
if (i%2 == 0) return 100;
else return 200;
break;
case 2: // binary decomposition method
if (Zy>0) return iColorOfExteriorUp;
else return iColorOfExteriorDown;
break;
} // switch
}
// if escaping stop iteration
i+=1;
}
// pixel is not escaping to infinity or not attracting to fixed attractore :
// change parameters : iterMax, distance ...
iUknownPixels+=1;
return iColorOfUnknown ; //
}
// plots raster point (ix,iy)
int PlotPoint(unsigned char A[] , unsigned int ix, unsigned int iy, int IterationMax, int iMethod)
{
unsigned i; /* index of 1D array */
unsigned char iColor;
i = Give_i(ix,iy); /* compute index of 1D array from indices of 2D array */
iColor = ComputeColor(ix, iy, IterationMax, iMethod);
A[i] = iColor;
return 0;
}
// fill array
// uses global var : ...
// scanning complex plane
int FillArray(unsigned char A[], int IterationMax, int iMethod )
{
unsigned int ix, iy; // pixel coordinate
printf("compute image \n");
// for all pixels of image
for(iy = iyMin; iy<=iyMax; ++iy)
{ printf(" %d z %d\n", iy, iyMax); //info
for(ix= ixMin; ix<=ixMax; ++ix) PlotPoint(A, ix, iy, IterationMax, iMethod ) ; //
}
return 0;
}
int ComputeBoundariesFromA2B(unsigned char A[], unsigned char B[])
{
unsigned int iX,iY; /* indices of 2D virtual array (image) = integer coordinate */
unsigned int i; /* index of 1D array */
/* sobel filter */
unsigned char G, Gh, Gv;
// boundaries are in edge array ( global var )
printf(" find boundaries in A array using Sobel filter\n");
// #pragma omp parallel for schedule(dynamic) private(i,iY,iX,Gv,Gh,G) shared(iyMax,ixMax, ER2)
for(iY=1;iY<iyMax-1;++iY){
for(iX=1;iX<ixMax-1;++iX){
Gv= A[Give_i(iX-1,iY+1)] + 2*A[Give_i(iX,iY+1)] + A[Give_i(iX-1,iY+1)] - A[Give_i(iX-1,iY-1)] - 2*A[Give_i(iX-1,iY)] - A[Give_i(iX+1,iY-1)];
Gh= A[Give_i(iX+1,iY+1)] + 2*A[Give_i(iX+1,iY)] + A[Give_i(iX-1,iY-1)] - A[Give_i(iX+1,iY-1)] - 2*A[Give_i(iX-1,iY)] - A[Give_i(iX-1,iY-1)];
G = sqrt(Gh*Gh + Gv*Gv);
i= Give_i(iX,iY); /* compute index of 1D array from indices of 2D array */
if (G==0) {B[i]=255;} /* background */
else {B[i]=0;} /* boundary */
}
}
return 0;
}
int CopyBoundariesFromA2B(unsigned char A[], unsigned char B[])
{
unsigned int iX,iY; /* indices of 2D virtual array (image) = integer coordinate */
unsigned int i; /* index of 1D array */
printf("copy boundaries from edge array to data array \n");
for(iY=1;iY<iyMax-1;++iY)
for(iX=1;iX<ixMax-1;++iX)
{i= Give_i(iX,iY); if (A[i]==0) B[i]=0;}
return 0;
}
// save "A" array to pgm file
int SaveArray2PGMFile( unsigned char A[], double k)
{
FILE * fp;
const unsigned int MaxColorComponentValue=255; /* color component is coded from 0 to 255 ; it is 8 bit color file */
char name [30]; /* name of file */
sprintf(name,"f%.0f", k); /* */
char *filename =strcat(name,".pgm");
char *comment="# Numerical approximation of Julia set for f(z)= z^2 after plane transformation; Adam Majewski";/* comment should start with # */
/* save image to the pgm file */
fp= fopen(filename,"wb"); /*create new file,give it a name and open it in binary mode */
fprintf(fp,"P5\n %s\n %u %u\n %u\n",comment,iWidth,iHeight,MaxColorComponentValue); /*write header to the file*/
fwrite(A,iSize,1,fp); /*write A array to the file in one step */
printf("File %s saved. \n", filename);
fclose(fp);
return 0;
}
int info()
{
// diplay info messages
printf("Numerical approximation of \n");
printf("Image Width = %f \n", ZxMax-ZxMin);
printf("PixelWidth = %f \n", PixelWidth);
printf("Maximal number of iterations = iterMax = %ld \n", iterMax);
printf("ratio of image = %f ; it should be 1.000 ...\n", ratio);
printf("Unknown pixels = %ld ; it should be 0 ...\n", iUknownPixels);
return 0;
}
/* ----------------------------------------- main -------------------------------------------------------------*/
int main()
{
setup();
FillArray(data, iterMax, 1 ); // level set method
SaveArray2PGMFile( data, iHeight+0); // save array data (components of Fatou set ) to pgm file
ComputeBoundariesFromA2B(data, edge1);
SaveArray2PGMFile( edge1, iHeight+1); // save array edge (Julia set ) to pgm file
FillArray(data, iterMax, 2 ); // binary decomposition method
SaveArray2PGMFile( data, iHeight+2); // save array data (components of Fatou set ) to pgm file
ComputeBoundariesFromA2B(data, edge);
SaveArray2PGMFile( edge, iHeight+3); // save array edge (Julia set ) to pgm file
CopyBoundariesFromA2B(edge1, edge); // boundary = boundary from LSM + boundary from BDM
SaveArray2PGMFile( edge, iHeight+4); // save array data (Julia set and components ) to pgm file
CopyBoundariesFromA2B(edge, data);
SaveArray2PGMFile( data, iHeight+5); // save array data (Julia set and components ) to pgm file
printf(" allways free memory to avoid buffer overflow \n");
free(data);
free(edge);
free(edge1);
info();
return 0;
}
Image magic code
convert f2005.pgm f.png
GIMP
Gimp was used for manually adding the numbers to the image
References
Λεζάντες
Items portrayed in this file
απεικονίζει
15 Απριλίου 2015
image/png
checksum Αγγλικά
9a9cf5d30655705e45d283f2fb5ce6d3d6a10456
data size Αγγλικά
49.922 Byte
2.000 εικονοστοιχείο
2.000 εικονοστοιχείο
Ιστορικό αρχείου
Κλικάρετε σε μια ημερομηνία/ώρα για να δείτε το αρχείο όπως εμφανιζόταν εκείνη τη στιγμή.
| Ώρα/Ημερομ. | Μικρογραφία | Διαστάσεις | Χρήστης | Σχόλια | |
|---|---|---|---|---|---|
| τελευταία | 13:59, 15 Απριλίου 2015 |  | 2.000 × 2.000 (49 KB) | Soul windsurfer | User created page with UploadWizard |
Συνδέσεις αρχείου
Τα παρακάτω λήμματα συνδέουν σε αυτό το αρχείο:
Καθολική χρήση αρχείου
Τα ακόλουθα άλλα wiki χρησιμοποιούν αυτό το αρχείο:
- Χρήση σε en.wikipedia.org
- Χρήση σε en.wikibooks.org
Μεταδεδομένα
Αυτό το αρχείο περιέχει πρόσθετες πληροφορίες, πιθανόν από την ψηφιακή φωτογραφική μηχανή ή το scanner που χρησιμοποιήθηκε για την δημιουργία ή την ψηφιοποίησή της. Αν το αρχείο έχει τροποποιηθεί από την αρχική του κατάσταση, ορισμένες λεπτομέρειες πιθανόν να μην αντιστοιχούν πλήρως στην τροποποιημένη εικόνα.
| Οριζόντια ανάλυση | 28,35 dpc |
|---|---|
| Κατακόρυφη ανάλυση | 28,35 dpc |
| Ημερομηνία και ώρα τελευταίας επεξεργασίας αρχείου | 13:53, 15 Απριλίου 2015 |