Ηλιακός χρόνος

Ηλιακός χρόνος ή ηλιακή ώρα ονομάζεται το σύστημα της μετρήσεως του περάσματος του χρόνου με βάση τη θέση του Ήλιου στον ουρανό. Η θεμελιώδης μονάδα για τον ηλιακό χρόνο είναι η ημέρα, με την έννοια του χρόνου της συνοδικής περιστροφής της Γης. Παραδοσιακά, υπάρχουν τρεις τύποι καθορισμού του χρόνου με βάση αστρονομικές παρατηρήσεις: ο αληθινός ηλιακός χρόνος, ο μέσος ηλιακός χρόνος και ο αστρικός χρόνος. Οι δύο πρώτοι εξετάζονται στο λήμμα αυτό, ενώ ο τρίτος βασίζεται στις κινήσεις των αστέρων αντί στην κίνηση του Ήλιου.[1]
Εισαγωγή
[Επεξεργασία | επεξεργασία κώδικα]
Μια κατακόρυφη ράβδος μεγάλου μήκους στερεωμένη στο έδαφος ρίχνει μια σκιά οποιαδήποτε αίθρια ημέρα. Σε μία συγκεκριμένη χρονική στιγμή της ημέρας η σκιά αυτή θα δείχνει ακριβώς προς τον βορρά ή προς τον νότο, ή θα εξαφανίζεται όταν και εάν ο Ήλιος βρίσκεται στο ζενίθ. Η στιγμή αυτή ονομάζεται αληθινή [τοπική] μεσημβρία (ή «αληθής μεσημβρία»), και αντιστοιχεί σε αληθινό ηλιακό χρόνο ή αληθή ηλιακή ώρα 12:00. Περίπου 24 ώρες αργότερα, η σκιά θα δείχνει και πάλι προς τον βορρά ή προς τον νότο, με τον Ήλιο να έχει καλύψει (φαινομενικά) ένα τόξο 360 μοιρών γύρω από τον γήινο άξονα. Τη στιγμή που ο Ήλιος έχει καλύψει ακριβώς 15 μοίρες (το 1/24 του κύκλου, με αμφότερες τις γωνίες να μετρούνται σε επίπεδο κάθετο ως προς τον άξονα της Γης), ο αληθινός ηλιακός χρόνος (ή αληθινή ηλιακή ώρα) είναι 13:00 ακριβώς, ενώ μετά από ακόμα 15 μοίρες θα είναι 14:00 ακριβώς.
Το πρόβλημα είναι ότι τον Σεπτέμβριο ο Ήλιος «χρειάζεται» μικρότερο χρονικό διάστημα (όπως αυτό μετρείται από ένα ακριβές χρονόμετρο) για να συμπληρώσει μια φαινομενική περιφορά από όσο τον Δεκέμβριο: 24 «ώρες» του ηλιακού χρόνου μπορεί να είναι κατά 21 δευτερόλεπτα μικρότερες ή κατά 29 δευτερόλεπτα μεγαλύτερες από ό,τι 24 ώρες σε χρόνο ρολογιού. Η μεταβολή αυτή δίνεται από τη λεγόμενη εξίσωση του χρόνου και οφείλεται στο ότι η τροχιά της Γης γύρω από τον Ήλιο δεν είναι κυκλική, αλλά έχει σχήμα ελλείψεως, καθώς και στο ότι ο άξονας περιστροφής της Γης δεν είναι κάθετος προς το επίπεδο της τροχιάς της γύρω από τον Ήλιο (υπάρχει η λεγόμενη λόξωση της εκλειπτικής).
Το αποτέλεσμα είναι ότι ένα ρολόι δεν μπορεί να ακολουθεί ακριβώς τον πραγματικό Ήλιο. Για τον λόγο αυτόν, επινοήθηκε ένας φανταστικός «μέσος Ήλιος», ο οποίος κινείται κατά μήκος του ουράνιου ισημερινού με σταθερό ρυθμό, που ισούται με τον μέσο ρυθμό του πραγματικού Ήλιο στη διάρκεια ενός έτους.[2] Ο χρόνος που αντιστοιχεί σε αυτόν τον μέσο Ήλιο είναι ο μέσος ηλιακός χρόνος. Ακόμα και αυτός δεν είναι τελείως σταθερός από τον έναν αιώνα στον άλλο, απλώς είναι σχετικώς ακριβής για πρακτικές εφαρμογές. Σήμερα μια μέση ηλιακή ημέρα έχει διάρκεια 86.400,002 δευτερόλεπτα, δηλαδή 24,0000006 ώρες.[3]
Αληθινός ηλιακός χρόνος
[Επεξεργασία | επεξεργασία κώδικα]Ο αληθινός Ήλιος είναι ο πραγματικός Ήλιος όπως τον βλέπει ένας παρατηρητής ευρισκόμενος στην επιφάνεια της Γηςh.[4] Ο αληθινός ηλιακός χρόνος ή αληθινή ηλιακή ώρα βασίζεται στην αληθινή κίνηση του πραγματικού Ήλιου. Βασίζεται στην έννοια της αληθινής ηλιακής ημέρας, που είναι το χρονικό διάστημα μεταξύ δύο διαδοχικών επιστροφών του Ήλιου στον ουράνιο μεσημβρινό του συγκεκριμένου τόπου.[5][6] Η αληθινή ηλιακή ώρα είναι αυτή που δείχνουν τα ηλιακά ωρολόγια, και αυτά πάλι όχι με μεγάλη ακρίβεια.
Η διάρκεια μιας αληθινής ηλιακής ημέρας μεταβάλλεται από μήνα σε μήνα όλο το έτος και το συσσωρευτικό αποτέλεσμα δίνει εποχικές διαφορές έως και 16 λεπτών του αληθινού από τον μέσο ηλιακό χρόνο. Καθώς προαναφέρθηκε, αυτό οφείλεται σε δύο λόγους:
- Στο ότι η τροχιά της Γης γύρω από τον Ήλιο δεν είναι κυκλική, αλλά έχει σχήμα ελλείψεως με τον Ήλιο στη μία εστία της ελλείψεως. Η Γη κινείται έτσι ταχύτερα όταν βρίσκεται πλησιέστερα στον Ήλιο (περιήλιο) και βραδύτερα όταν όταν απέχει περισσότερο από τον Ήλιο (αφήλιο) (σύμφωνα με τον Τρίτο νόμο του Κέπλερ).
- Στο ότι ο άξονας περιστροφής της Γης δεν είναι κάθετος προς το επίπεδο της τροχιάς της γύρω από τον Ήλιο. Υπάρχει η λεγόμενη λόξωση της εκλειπτικής, μια γωνία ανάμεσα στον ουράνιο ισημερινό και τη φαινομενική τροχιά του Ήλιου στην ουράνια σφαίρα κατά τη διάρκεια του έτους. Όταν ο Ήλιος διασχίζει τον ουράνιο ισημερινό, σε αμφότερες τις ισημερίες, η ημερήσια μετατόπισή του (σε σχέση με τους μακρινούς αστέρες) σχηματίζει τη μέγιστη αυτή γωνία με τον ουράνιο ισημερινό, οπότε η προβολή αυτής της μετατοπίσεως πάνω στον ουράνιο ισημερινό είναι μικρότερη από τη μέση τιμή της για όλο το έτος. Αντιθέτως, όταν ο Ήλιος βρίσκεται σε μέγιστη γωνιακή απόσταση από τον ουράνιο ισημερινό, σε αμφότερα τα ηλιοστάσια, η ημερήσια μετατόπιση του Ήλιου είναι παράλληλη προς τον ουράνιο ισημερινό, οπότε η προβολή αυτής της μετατοπίσεως πάνω στον ουράνιο ισημερινό είναι μέγιστη, μεγαλύτερη από τη μέση τιμή της για όλο το έτος (δείτε το λήμμα τροπικό έτος).
| Ημερομηνία | Διάρκεια σε μέσο ηλιακό χρόνο |
|---|---|
| 11 Φεβρουαρίου | 24 ώρες |
| 26 Μαρτίου | 24 ώρες − 18,1 δευτερόλεπτα |
| 14 Μαΐου | 24 ώρες |
| 19 Ιουνίου | 24 ώρες + 13,1 δευτερόλεπτα |
| 25/26 Ιουλίου | 24 ώρες |
| 16 Σεπτεμβρίου | 24 ώρες − 21,3 δευτερόλεπτα |
| 2/3 Νοεμβρίου | 24 ώρες |
| 22 Δεκεμβρίου | 24 ώρες + 29,9 δευτερόλεπτα |
Οι διάρκειες αυτές μεταβάλλονται αργά, με μεταβολές που γίνονται αντιληπτές σε λίγες χιλιάδες έτη.
Μέσος ηλιακός χρόνος
[Επεξεργασία | επεξεργασία κώδικα]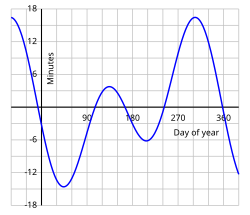
Ο μέσος ηλιακός χρόνος ορίζεται ως η ωρική γωνία του μέσου Ήλιου συν 12 ώρες. Αυτή η μετάθεση κατά 12 ώρες προήλθε από την απόφαση η κάθε ημέρα να αρχίζει τα μεσάνυχτα για πρακτικούς σκοπούς, ενώ η ωρική γωνία ή η θέση του μέσου Ήλιου μετρείται από τον τοπικό μεσημβρινό.[8] Σήμερα ο μέσος ηλιακός χρόνος είναι προτυποποιημένος με βάση τον παγκόσμιο χρόνο UT1, που έχει κατασκευασθεί μαθηματικώς από παρατηρήσεις συμβολομετρίας πολύ μεγάλης γραμμής βάσεως των ημερήσιων κινήσεων ραδιοπηγών που βρίσκονται σε άλλους γαλαξίες, και από άλλες αστρονομικές παρατηρήσεις.[9]:68,326[10] Η διάρκεια του φωτός της ημέρας μεταβάλλεται μέσα στο έτος, αλλά η διάρκεια μιας μέσης ηλιακής ημέρας είναι σχεδόν σταθερή, αντίθετα με τη διάρκεια μιας αληθινής ηλιακής ημέρας. Μία αληθινή ηλιακή ημέρα μπορεί να είναι από 20 δευτερόλεπτα βραχύτερη έως 30 δευτερόλεπτα μακρύτερη από μια μέση ηλιακή ημέρα.[7][11] Οι μακρύτερες ή οι βραχύτερες ημέρες έρχονται σε ομάδες, οπότε η διαφορά αυτή συσσωρεύεται μέχρι που ο μέσος χρόνος να προηγείται του αληθινού κατά περίπου 14 λεπτά κοντά στις 6 Φεβρουαρίου και να έπεται αυτού κατά περίπου 16 λεπτά κοντά στις 3 Νοεμβρίου. Η εξίσωση του χρόνου υποδηλώνει ακριβώς αυτή τη διαφορά, η οποία αυξομειώνεται περιοδικά και δεν συσσωρεύεται από έτους σε έτος.
Ο μέσος ηλιακός χρόνος ακολουθεί τον μέσο Ήλιο. Ο Ζαν Μεές περιγράφει τον μέσο Ήλιο ως εξής:
«Ας θεωρήσουμε έναν πρώτο υποθετικό Ήλιο που κινείται κατά μήκος της εκλειπτικής με σταθερή ταχύτητα και που συμπίπτει με τον πραγματικό Ήλιο στο περίγειο και στο απόγειο (όταν η Γη βρίσκεται στο περιήλιο και στο αφήλιο αντιστοίχως). Κατόπιν ας θεωρήσουμε έναν δεύτερο υποθετικό Ήλιο, που κινείται κατά μήκος του ουράνιου ισημερινού με σταθερή ταχύτητα και συμπίπτει με τον πρώτο υποθετικό Ήλιο στις ισημερίες. Αυτός ο δεύτερος φανταστικός Ήλιος είναι ο μέσος Ήλιος».[12]
Το μήκος (διάρκεια) της μέσης ηλιακής ημέρας αυξάνεται αργά με την πάροδο των αιώνων εξαιτίας της παλιρροιακής επιταχύνσεως της Σελήνης από τη Γη και την αντίστοιχη επιβράδυνση της περιστροφής της Γης.
Ιστορία
[Επεξεργασία | επεξεργασία κώδικα]
Ο ήλιος ήταν ανέκαθεν ορατός στον γήινο ουρανό και η θέση του είναι η βάση του αληθούς ηλιακού χρόνου, που ήταν η «ώρα» που χρησιμοποιούσαν στην αρχαιότητα. Κάποιες από τις πρώτες μεθόδους προσδιορισμού της θέσεως του ήλιου μάς υποδεικνύονται από έναν αιγυπτιακό οβελίσκο του 3500 π.Χ. περίπου[13], από έναν κινεζικό γνώμονα του 2300 π.Χ.[14] και από ένα αιγυπτιακό ηλιακό ρολόι του 1500 π.Χ.[15].
Οι Βαβυλώνιοι αστρονόμοι γνώριζαν ότι οι ώρες του φωτός της ημέρας αυξομειώνονταν σε όλη τη διάρκεια του έτους. Μια πινακίδα του 649 π.Χ. δείχνει ότι είχαν υιοθετήσει τον λόγο 2:1 της μεγαλύτερης ως προς τη βραχύτερη ημέρα και εκτιμούσαν τη διακύμανση με χρήση μιας γραμμικής συναρτήσεως «ζιγκ-ζαγκ».[16] Δεν είναι σαφές το εάν γνώριζαν την εξίσωση του χρόνου. Ο Κλαύδιος Πτολεμαίος ξεχωρίζει ξεκάθαρα τη μέση από την αληθή ηλιακή ημέρα στην Αλμαγέστη (2ος αιώνας μ.Χ.), και παραθέτει τιμές από την εξίσωση του χρόνου στους πίνακές του.[17]
Ο αληθής ηλιακός χρόνος/ώρα γινόταν λιγότερο χρήσιμος καθώς το εμπόριο αυξανόταν και τα μηχανικά ρολόγια βελτιώνονταν. Ο μέσος ηλιακός χρόνος εισάχθηκε σε αλμανάκ στην Αγγλία το 1834 και στη Γαλλία το 1835. Επειδή η ακριβής θέση του Ήλιου ήταν δύσκολο να προσδιορισθεί απευθείας εξαιτίας της μεγάλης γωνιακής διαμέτρου του στον ουρανό, 0 μέσος ηλιακός χρόνος προσδιοριζόταν ως μια σταθερή αναλογία χρόνου από την παρατήρηση απλανών (μακρινών) αστέρων, που αποτελούν πρακτικά σημειακές πηγές φωτός. Ξεχώρισε ένα συγκεκριμένο πρότυπο για την έναρξη της μέσης ηλιακής ώρας από τα μεσάνυχτα, που άρχισε να αποκαλείται «Παγκόσμιος Χρόνος».[9]:9–11
Εννοιολογικώς, ο Παγκόσμιος χρόνος καθορίζεται από την περιστροφή της Γης γύρω από τον Ήλιο και επομένως είναι ένας μέσος ηλιακός χρόνος. Ωστόσο ο UT1, το πρότυπό του σε κοινή χρήση από το 1955, εφαρμόζει έναν ελαφρώς διαφορετικό ορισμό της περιστροφής, με διόρθωση για την κίνηση των πόλων της Γης κατά την περιστροφή της. Η διαφορά μεταξύ του διορθωμένου αυτού μέσου ηλιακού χρόνου και του Συντονισμένου Παγκόσμιου Χρόνου (UTC) καθορίζει το εάν χρειάζεται να εισαχθεί ένα εμβόλιμο δευτερόλεπτο. (Από το 1972 η χρονική κλίμακα του UTC εκφράζεται σε δευτερόλεπτα του Διεθνούς συστήματος μονάδων (SI), και το δευτερόλεπτο αυτό ήταν ήδη λίγο βραχύτερο από την τιμή του δευτερολέπτου του μέσου ηλιακού χρόνου.[18][9]:227–231)
Δείτε επίσης
[Επεξεργασία | επεξεργασία κώδικα]
Παραπομπές
[Επεξεργασία | επεξεργασία κώδικα]- ↑ Connaissance des Temps, 1902, σελ. 759 Αρχειοθετήθηκε August 10, 2011, στο Wayback Machine..
- ↑ «solar time, mean». Glossary, Astronomical Almanac Online. Her Majesty's Nautical Almanac Office and the United States Naval Observatory. 2021.
- ↑ «Leap Seconds». Time Service Department, United States Naval Observatory. 1999. Αρχειοθετήθηκε από το πρωτότυπο στις 12 Μαρτίου 2015.
- ↑ Tatum, J.B. (27 Μαρτίου 2022). «Celestial Mechanics Chapter 6» (PDF). University of Victoria. Αρχειοθετήθηκε (PDF) από το πρωτότυπο στις 23 Σεπτεμβρίου 2015.
- ↑ «solar time, apparent». Glossary, Astronomical Almanac Online. Her Majesty's Nautical Almanac Office and the U.S. Naval Observatory. 2021.
- ↑ Yallop, B.D.· Hohenker, C.Y. (Αύγουστος 1989). «Astronomical Information Sheet No. 58» (PDF). HM Nautical Almanac Office. Solar Location Diagram. Αρχειοθετήθηκε από το πρωτότυπο (PDF) στις 23 Δεκεμβρίου 2022. Ανακτήθηκε στις 15 Μαΐου 2024.
- ↑ 7,0 7,1 Jean Meeus: Mathematical astronomy morsels, εκδ. Willmann-Bell, Richmond 1997, σελ. 346
- ↑ Hilton, James L.· McCarthy, Dennis D. (2013). «Precession, Nutation, Polar Motion and Earth Rotation». Στο: Urban, Sean E.· Seidelmann, P. Kenneth, επιμ. Explanatory Supplement to the Astronomical Almanac (3η έκδοση). Mill Valley, CA: University Science Books. ISBN 978-1-891389-85-6.
- ↑ 9,0 9,1 9,2 McCarthy, D.D.· Seidelmann, P.K. (2009). TIME From Earth Rotation to Atomic Physics. Weinheim: Wiley-VCH Verlag GmbH & Co. KGa. ISBN 978-3-527-40780-4.
- ↑ Capitaine, N.; Wallace, P.T.; McCarthy, D.D. (2003). «Expressions to implement the IAU 2000 definition of UT1». Astronomy and Astrophysics 406 (3): 1135-1149. doi:. Bibcode: 2003A&A...406.1135C. http://www.aanda.org/index.php?option=article&access=bibcode&bibcode=2003A%2526A...406.1135CFUL.
- ↑ Ricci, Pierpaolo. «The duration of the true solar day». pierpaoloricci.it. Αρχειοθετήθηκε από το πρωτότυπο στις 26 Αυγούστου 2009.
- ↑ Meeus, J.: Astronomical Algorithms, 2η έκδ., Willmann-Bell, Richmond 1998, σελ. 183
- ↑ «A Walk Through Time - Early Clocks». A Walk Through Time - The Evolution of Time Measurement through the Ages. National Institute of Standards and Technology. 12 Αυγούστου 2009.
- ↑ Li, Geng (2015). «Gnomons in Ancient China». Στο: Ruggles, C., επιμ. Handbook of Archaeoastronomy and Ethnoastronomy. σελίδες 2095–2104. Bibcode:2015hae..book.2095L. doi:10.1007/978-1-4614-6141-8_219. ISBN 978-1-4614-6140-1.
- ↑ Vodolazhskaya, L.N. (2014). «Reconstruction of ancient Egyptian sundials». Archaeoastronomy and Ancient Technologies 2 (2): 1–18. http://aaatec.org/documents/article/vl4.pdf.
- ↑ Pingree, David; Reiner, Erica (1974). «A Neo-Babylonian Report on Seasonal Hours». Archiv für Orientforschung 25: 50-55. ISSN 0066-6440. https://www.jstor.org/stable/41636303.
- ↑ Neugebauer, Otto (1975), A History of Ancient Mathematical Astronomy, Νέα Υόρκη / Χαϊδελβέργη / Βερολίνο: Springer-Verlag, σελ. 984-986, ISBN 978-0-387-06995-1
- ↑ (1) Στο άρθρο με τίτλο «The Physical Basis of the Leap Second» των D.D. McCarthy, C. Hackman και R.A. Nelson στο Astronomical Journal, τόμ. 136 (2008), σσ. 1906-1908, δηλώνεται (σελ. 1908) ότι «το δευτερόλεπτο του SI είναι ισοδύναμο με μια παλαιότερη μέτρηση του δευτερολέπτου του UT1, που ήταν ήδη εξαρχής υπερβολικά μικρό, και επιπλέον, καθώς η διάρκεια του UT1 αυξάνεται, η μεταξύ τους διαφορά αυξάνεται». (2) Στα τέλη της δεκαετίας του 1950 το πρότυπο του καισίου εφαρμοζόταν για τη μέτρηση και ορισμό της διάρκειας του δευτερολέπτου του μέσου ηλιακού χρόνου (UT2) (9.192.631.830 κύκλοι), καθώς και του δευτερολέπτου του χρόνου εφημερίδας (ET) (9.192.631.770 ± 20 κύκλοι), δείτε το «Time Scales» του L. Essen Αρχειοθετήθηκε October 19, 2008, στο Wayback Machine., στο Metrologia, τόμ. 4 (1968), σσ. 161-165, στη σελ. 162. Ως γνωστόν, η τιμή των 9.192.631.770 κύκλων επιλέχθηκε για τη διάρκεια του δευτερολέπτου του SI. Ο L. Essen στο ίδιο άρθρο το 1968 (σελ.162) γράφει ότι «αυτό φαινόταν δικαιολογημένο αν λάβουμε υπόψη τις διακυμάνσεις στον UT2».
Εξωτερικοί σύνδεσμοι
[Επεξεργασία | επεξεργασία κώδικα]- Ανατολή, δύση και μέγιστο ύψος του Ήλιου στον ουρανό για κάθε ημέρα του έτους και για κάθε τόπο της Γης
- Astrarium Solar Tempometer: Αληθείς ηλιακές ώρες (υπολογισμός)
