Μετάβαση στο περιεχόμενο

Πυραμίδα (γεωμετρία)

Από τη Βικιπαίδεια, την ελεύθερη εγκυκλοπαίδεια
(Ανακατεύθυνση από Πυραμίδα)
Παράδειγμα πυραμίδας με τετραγωνική βάση

Η πυραμίδα είναι γεωμετρικό στερεό. Είναι πολύεδρο που σχηματίζεται με ένα κανονικό ν-γωνο ως βάση και ν τριγωνικές πλευρές που συνδέονται σε μια κορυφή. Η πιο γνωστή μορφή πυραμίδας (και αυτή που εννοείται συνήθως) είναι αυτή με πέντε πλευρές (επιφάνειες), και οκτώ ακμές, με τετράγωνο ως βάση και τέσσερα ισοσκελή και ίσα μεταξύ τους τρίγωνα ως πλευρές.

Ο όγκος μιας πυραμίδας δίνεται από τον τύπο , όπου Α το εμβαδό της βάσης και υ το ύψος από τη βάση στην κορυφή.

Ένα από τα Πλατωνικά στερεά, το τετράεδρο, είναι πυραμίδα με όλες τις πλευρές της ισόπλευρα τρίγωνα.

Λόγω του σχήματός της η πυραμίδα έχει κάποιες ασυνήθιστες ιδιότητες όπως, για παράδειγμα, για να εμφανίζει σκιά, η πηγή του φωτός θα πρέπει να είναι αρκετά χαμηλά (συγκριτικά με τις διαστάσεις της πυραμίδας).

Ετυμολογία

[Επεξεργασία | επεξεργασία κώδικα]

Η λέξη «πυραμίδα» προέρχεται από την αρχαιοελληνική λέξη «πυραμίς» (πυράμις), η οποία αναφερόταν σε μια δομή σε σχήμα πυραμίδας και σε ένα είδος κέικ σιταριού[1][2]]. Ο όρος έχει τις ρίζες του στα ελληνικά «πυρ» (πυρ, 'φωτιά') και «άμις» (άμις, 'δοχείο'), τονίζοντας την αιχμηρή, φλογερή εμφάνιση του σχήματος[3].

Στη Μεσαιωνική ελληνική γλώσσα, ο όρος εξελίχθηκε σε «πυραμίδα» (pyramída), συνεχίζοντας να δηλώνει τις πυραμιδικές κατασκευές[4]. Ο όρος «πυραμίδα» επηρέασε την εξέλιξη της λέξης σε «πυραμίδα» στα αγγλικά και σε άλλες γλώσσες[5][6].

Ορισμός

[Επεξεργασία | επεξεργασία κώδικα]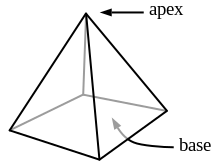
Μέρη μιας πυραμίδας

Η πυραμίδα είναι ένα πολύεδρο που μπορεί να σχηματιστεί με τη σύνδεση μιας πολυγωνικής βάσης και ενός σημείου, που ονομάζεται κορυφή. Κάθε ακμή της βάσης και της κορυφής σχηματίζουν ένα ισοσκελές τρίγωνο, που ονομάζεται πλευρική όψη.[7] Οι ακμές που συνδέονται από τις κορυφές της πολυγωνικής βάσης με την κορυφή ονομάζονται πλευρικές ακμές[8] Ιστορικά, ο ορισμός της πυραμίδας έχει περιγραφεί από πολλούς μαθηματικούς στην αρχαιότητα. Ο Ευκλείδης στα Στοιχεία του όρισε την πυραμίδα ως ένα στερεό σχήμα, κατασκευασμένο από ένα επίπεδο σε ένα σημείο. Το πλαίσιο του ορισμού του ήταν ασαφές, μέχρι που ο Ήρων ο Αλεξανδρεύς την όρισε ως το σχήμα με την τοποθέτηση του σημείου μαζί με μια πολυγωνική βάση[9].

Ως πρισματοειδές ορίζεται ένα πολύεδρο όπου οι κορυφές του βρίσκονται σε δύο παράλληλα επίπεδα, ενώ οι πλευρικές του επιφάνειες είναι τρίγωνα, τραπέζια και παραλληλόγραμμα[10]. Οι πυραμίδες κατατάσσονται στα πρισματοειδή[11].

Ταξινόμηση και τύποι

[Επεξεργασία | επεξεργασία κώδικα]
Η οικογένεια μιας κανονικής πολυγωνικής πυραμίδας βάσης: τετράεδρο, τετραγωνική πυραμίδα, πενταγωνική πυραμίδα και εξαγωνική πυραμίδα.

Η ορθή πυραμίδα είναι μια πυραμίδα της οποίας η βάση περιγράφεται γύρω από τον κύκλο και το ύψος της πυραμίδας συναντά το κέντρο του κύκλου[12]. Αυτή η πυραμίδα μπορεί να ταξινομηθεί με βάση την κανονικότητα των βάσεων της. Μια πυραμίδα με βάση ένα κανονικό πολύγωνο ονομάζεται κανονική πυραμίδα[13]. Για την πυραμίδα με κανονική βάση με n όψεις, έχει n + 1 κορυφές, n + 1 όψεις και 2n ακμές. [14] Μια τέτοια πυραμίδα έχει ισοσκελή τρίγωνα ως όψεις, με τη συμμετρία της να είναι Cnv, μια συμμετρία τάξης 2n: οι πυραμίδες είναι συμμετρικές καθώς περιστρέφονται γύρω από τον άξονα συμμετρίας τους (μια ευθεία που διέρχεται από την κορυφή και το κεντροειδές της βάσης), και είναι κατοπτρικά συμμετρικές σε σχέση με οποιοδήποτε κάθετο επίπεδο που διέρχεται από μια διχοτόμο της βάσης. [15][16] Ενδεικτικά παραδείγματα είναι η τετραγωνική πυραμίδα και η πενταγωνική πυραμίδα, μια πυραμίδα με τέσσερις και πέντε τριγωνικές επιφάνειες με βάση τετράγωνο και πεντάγωνο, αντίστοιχα- ταξινομούνται ως το πρώτο και το δεύτερο στερεό Τζόνσον αν οι κανονικές τους επιφάνειες και ακμές που έχουν ίσο μήκος και οι συμμετρίες τους είναι C4v τάξης 8 και C5v τάξης 10, αντίστοιχα. [17][18] . Ένα τετράεδρο ή τριγωνική πυραμίδα είναι ένα παράδειγμα που έχει τέσσερα ισόπλευρα τρίγωνα, με όλες τις ακμές ίσου μήκους, και ένα από αυτά θεωρείται ως βάση. Επειδή οι επιφάνειες είναι κανονικές, αποτελεί παράδειγμα πλατωνικού στερεού και δέλταεδρου και έχει τετραεδρική συμμετρία [19][20]. Μια πυραμίδα με τη βάση της ως κύκλο είναι γνωστή ως κώνος [21] Οι πυραμίδες έχουν την ιδιότητα του αυτο-δυϊκού, δηλαδή οι δυϊκές τους είναι ίδιες με τις κορυφές που αντιστοιχούν στις ακμές και αντίστροφα[22]. Ο σκελετός τους μπορεί να αναπαρασταθεί ως γράφημα τροχού[23]

Πυραμίδες με ορθογώνιες και ρομβικές βάσεις

Μια ορθή πυραμίδα μπορεί επίσης να έχει βάση με ακανόνιστο πολύγωνο. παραδείγματος χάριν, οι πυραμίδες με ορθογώνιο και ρόμβο ως βάσεις. Αυτές οι δύο πυραμίδες έχουν συμμετρία C2v τάξης 4.

Πυραμίδα που κόβεται από κεκλιμένο επίπεδο
Μια πυραμίδα με βάση το πεντάγραμμο.

Ο τύπος των πυραμίδων μπορεί να προκύψει με πολλούς τρόπους. Η κανονικότητα της βάσης μιας πυραμίδας μπορεί να ταξινομηθεί με βάση τον τύπο του πολυγώνου, και ένα παράδειγμα είναι η πυραμίδα με κανονικό πολύγωνο αστέρι ως βάση, γνωστή ως πυραμίδα αστέρι [24]. Η πυραμίδα που αποκόπτεται από ένα επίπεδο ονομάζεται αποκομμένη πυραμίδα- αν το επίπεδο αποκοπής είναι παράλληλο με τη βάση μιας πυραμίδας, ονομάζεται "κόλουρη".

Μέτρηση

[Επεξεργασία | επεξεργασία κώδικα]

Το εμβαδόν της επιφάνειας είναι το συνολικό εμβαδόν των επιφανειών κάθε πολυέδρου. Στην περίπτωση μιας πυραμίδας, το εμβαδόν της επιφάνειάς της είναι το άθροισμα του εμβαδού των τριγώνων και του εμβαδού της πολυγωνικής βάσης.

Ο όγκος μιας πυραμίδας είναι το γινόμενο του ενός τρίτου του εμβαδού της βάσης και του ύψους. Δεδομένου ότι είναι το εμβαδόν της βάσης και είναι το ύψος μιας πυραμίδας. Μαθηματικά, ο όγκος μιας πυραμίδας είναι:[25]

Ο όγκος μιας πυραμίδας καταγράφηκε ήδη στην αρχαία Αίγυπτο, όπου υπολόγισαν τον όγκο ενός τετραγωνικού κόλουρης, γεγονός που υποδηλώνει ότι γνώριζαν τον όγκο μιας τετραγωνικής πυραμίδας[26]. Ο τύπος του όγκου για μια γενική πυραμίδα ανακαλύφθηκε από τον Ινδό μαθηματικό Αριαμπχάτα, όπου ανέφερε στο έργο του Αριαμπχάτιγια ότι ο όγκος μιας πυραμίδας είναι λανθασμένα το μισό γινόμενο της βάσης της περιοχής και του ύψους [27].

Γενίκευση

[Επεξεργασία | επεξεργασία κώδικα]
Υπερπυραμίδα 4 διαστάσεων με βάση έναν κύβο

Η υπερπυραμίδα είναι η γενίκευση της πυραμίδας στον n-διάστατο χώρο. Στην περίπτωση της πυραμίδας, συνδέουμε όλες τις κορυφές της βάσης, ένα πολύγωνο σε ένα επίπεδο, με ένα σημείο εκτός του επιπέδου, το οποίο είναι η κορυφή. Το ύψος της πυραμίδας είναι η απόσταση της κορυφής από το επίπεδο. Αυτή η κατασκευή γενικεύεται σε n διαστάσεις. Η βάση γίνεται ένα (n − 1)--πολυτόπιο σε ένα (n − 1)-διάστατο υπερεπίπεδο. Ένα σημείο που ονομάζεται κορυφή βρίσκεται έξω από το υπερεπίπεδο και συνδέεται με όλες τις κορυφές του πολυτόπου και η απόσταση της κορυφής από το υπερεπίπεδο ονομάζεται ύψος [28].

Ο n-διάστατος όγκος μιας n-διάστατης υπερπυραμίδας μπορεί να υπολογιστεί ως εξής:

Εδώ Vn υποδηλώνει τον n-διαστατικό όγκο της υπερπυραμίδας.A συμβολίζει τον (n - 1)- διαστατικό όγκο της βάσης και h το ύψος, δηλαδή την απόσταση μεταξύ της κορυφής και του (n − 1)-διάστατο υπερεπίπεδο που περιέχει τη βάση A. [28]

Δείτε επίσης

[Επεξεργασία | επεξεργασία κώδικα]

Παραπομπές

[Επεξεργασία | επεξεργασία κώδικα]
  1. ↑ Henry George Liddell, Robert Scott, A Greek-English Lexicon, πυραμίς, https://www.perseus.tufts.edu/hopper/text?doc=Perseus%3Atext%3A1999.04.0057%3Aentry%3Dpurami%2Fs .
  2. ↑ The word meant "a kind of cake of roasted wheat-grains preserved in honey"; the Egyptian pyramids were named after its form. See Beekes, Robert S. (2009), Etymological Dictionary of Greek, Brill, σελ. 1261 .
  3. ↑ Liddell, Henry George· Scott, Robert (1940). A Greek–English Lexicon. Clarendon Press. 
  4. ↑ «πυραμίδα». Wiktionary. 12 Ιουλίου 2022. Ανακτήθηκε στις 30 Ιουνίου 2024. 
  5. ↑ Lewis, Charlton T.· Short, Charles (1879). A Latin Dictionary. Clarendon Press. 
  6. ↑ Peck, Harry Thurston (1898). Harper's Dictionary of Classical Antiquities. Harper & Brothers. 
  7. ↑ Cromwell, Peter R. (1997), Polyhedra, Cambridge University Press, σελ. 13, https://archive.org/details/polyhedra0000crom/page/13/mode/2up?view=theater .
  8. ↑ Smith, James T. (2000), Methods of Geometry, John Wiley & Sons, σελ. 98, ISBN 0-471-25183-6, https://books.google.com/books?id=B0khWEZmOlwC&pg=PA98 .
  9. ↑ Heath, Thomas (1908), Euclid: The Thirteen Books of the Elements, 3, Cambridge University Press, σελ. 268, https://archive.org/details/euclids-elements-vol.-3/page/268/mode/1up?view=theater .
  10. ↑ Alsina, Claudi; Nelsen, Roger B. (2015), A Mathematical Space Odyssey: Solid Geometry in the 21st Century, Mathematical Association of America, σελ. 85, ISBN 978-0-88385-358-0, https://books.google.com/books?id=FEl2CgAAQBAJ&pg=PA85 .
  11. ↑ Grünbaum, Branko (1997), «Isogonal Prismatoids», Discrete & Computational Geometry 18: 13–52, doi:10.1007/PL00009307 .
  12. ↑ Polya, G. (1954), Mathematics and Plausible Reasoning: Induction and analogy in mathematics, Princeton University Press, σελ. 138, ISBN 0-691-02509-6, https://books.google.com/books?id=-TWTcSa19jkC&pg=PA138 .
  13. ↑ O'Leary, Michael (2010), Revolutions of Geometry, John Wiley & Sons, σελ. 10, ISBN 978-0-470-59179-6, https://books.google.com/books?id=Ch5CrMtyniEC&pg=PA10 .
  14. ↑ Humble, Steve (2016), The Experimenter's A-Z of Mathematics: Math Activities with Computer Support, Taylor & Francis, σελ. 23, ISBN 978-1-134-13953-8, https://books.google.com/books?id=S-80DwAAQBAJ&pg=PA23 .
  15. ↑ Johnson, Norman W. (2018), Geometries and Transformations, Cambridge University Press, ISBN 978-1-107-10340-5 . See Chapter 11: Finite Symmetry Groups, 11.3 Pyramids, Prisms, and Antiprisms.
  16. ↑ Alexandroff, Paul (2012), An Introduction to the Theory of Groups, Dover Publications, σελ. 48, ISBN 978-0-486-48813-4, https://books.google.com/books?id=DPrDAgAAQBAJ&pg=PA48 .
  17. ↑ Johnson, Norman W. (1966), «Convex polyhedra with regular faces», Canadian Journal of Mathematics 18: 169–200, doi:10.4153/cjm-1966-021-8,
    Zbl 0132.14603
     . See table III, line 1.
  18. ↑ Uehara, Ryuhei (2020), Introduction to Computational Origami: The World of New Computational Geometry, Springer, σελ. 62, doi:10.1007/978-981-15-4470-5, ISBN 978-981-15-4470-5, https://books.google.com/books?id=51juDwAAQBAJ&pg=PA62 .
  19. ↑ Shavinina, Larisa V. (2013), The Routledge International Handbook of Innovation Education, Routledge, σελ. 333, ISBN 978-0-203-38714-6, https://books.google.com/books?id=JcPd_JRc4FgC&pg=PA333 .
  20. ↑ Cundy, H. Martyn (1952), «Deltahedra», The Mathematical Gazette 36 (318): 263–266, doi:10.2307/3608204 .
  21. ↑ Kelley, W. Michael (2009), The Humongous Book of Geometry Problems, Penguin Group, σελ. 455, ISBN 978-1-61564-698-2, https://books.google.com/books?id=3XSjAQAAQBAJ&pg=PA455 .
  22. ↑ Wohlleben, Eva (2019), «Duality in Non-Polyhedral Bodies Part I: Polyliner», στο: Cocchiarella, Luigi, επιμ., ICGG 2018 - Proceedings of the 18th International Conference on Geometry and Graphics: 40th Anniversary - Milan, Italy, August 3-7, 2018, Advances in Intelligent Systems and Computing, 809, Springer, σελ. 485–486, doi:10.1007/978-3-319-95588-9, ISBN 978-3-319-95588-9, https://books.google.com/books?id=rEpjDwAAQBAJ&pg=PA485 
  23. ↑ Pisanski, Tomaž; Servatius, Brigitte (2013), Configuration from a Graphical Viewpoint, Springer, σελ. 21, doi:10.1007/978-0-8176-8364-1, ISBN 978-0-8176-8363-4, https://books.google.com/books?id=3vnEcMCx0HkC&pg=PA21 .
  24. ↑ Wenninger, Magnus J. (1974), Polyhedron Models, Cambridge University Press, σελ. 50, ISBN 978-0-521-09859-5, https://books.google.com/books?id=N8lX2T-4njIC&pg=PA50 
  25. ↑ Alexander, Daniel C.; Koeberlin, Geralyn M. (2014), Elementary Geometry for College Students (6th έκδοση), Cengage Learning, σελ. 403, ISBN 978-1-285-19569-8, https://books.google.com/books?id=EN_KAgAAQBAJ&pg=PA403 .
  26. ↑ Gillings, R. J. (1964), «The volume of a truncated pyramid in ancient Egyptian papyri», The Mathematics Teacher 57 (8): 552–555, doi:10.5951/MT.57.8.0552 .
  27. ↑ Cajori, Florian (1991), History of Mathematics (5th έκδοση), American Mathematical Society, σελ. 87, ISBN 978-1-4704-7059-3, https://books.google.com/books?id=0BZuEAAAQBAJ&pg=PA87 .
  28. ↑ 28,0 28,1 Mathai, A. M. (1999), An Introduction to Geometrical Probability: Distributional Aspects with Applications, Taylor & Francis, σελ. 42–43, ISBN 978-90-5699-681-9, https://books.google.com/books?id=FV6XncZgfcwC&pg=PA43 .
Ανακτήθηκε από "https://el.wikipedia.org/w/index.php?title=Πυραμίδα_(γεωμετρία)&oldid=10809139"