Μετάβαση στο περιεχόμενο

Πειραματικός σχεδιασμός

Από τη Βικιπαίδεια, την ελεύθερη εγκυκλοπαίδεια
Πειραματικός σχεδιασμός με πλήρη παραγοντικό σχεδιασμό (αριστερά), επιφάνεια απόκρισης με πολυώνυμο δευτέρου βαθμού (δεξιά)

Ο πειραματικός σχεδιασμός (DOE),[1]επίσης γνωστός ως σχεδιασμός πειράματος, είναι ο σχεδιασμός οποιασδήποτε εργασίας που αποσκοπεί στην περιγραφή και την εξήγηση της μεταβολής των πληροφοριών υπό συνθήκες που υποτίθεται ότι αντικατοπτρίζουν τη μεταβολή. Ο όρος συνδέεται γενικά με πειράματα στα οποία ο σχεδιασμός εισάγει συνθήκες που επηρεάζουν άμεσα τη μεταβολή, αλλά μπορεί επίσης να αναφέρεται στο σχεδιασμό οιονεί πειραμάτων, στα οποία επιλέγονται για παρατήρηση φυσικές συνθήκες που επηρεάζουν τη μεταβολή.

Στην απλούστερη μορφή του, ένα πείραμα αποσκοπεί στην πρόβλεψη του αποτελέσματος με την εισαγωγή μιας αλλαγής των προϋποθέσεων, η οποία αντιπροσωπεύεται από μία ή περισσότερες ανεξάρτητες μεταβλητές, που αναφέρονται επίσης ως "μεταβλητές εισόδου" ή "μεταβλητές[2] πρόβλεψης". Η αλλαγή σε μία ή περισσότερες ανεξάρτητες μεταβλητές υποτίθεται γενικά ότι θα οδηγήσει σε αλλαγή σε μία ή περισσότερες εξαρτημένες μεταβλητές, που αναφέρονται επίσης ως "μεταβλητές εξόδου" ή "μεταβλητές απόκρισης". Ο πειραματικός σχεδιασμός μπορεί επίσης να προσδιορίζει μεταβλητές ελέγχου που πρέπει να διατηρούνται σταθερές για να αποτραπεί η επίδραση εξωτερικών παραγόντων στα αποτελέσματα. Ο πειραματικός σχεδιασμός περιλαμβάνει όχι μόνο την επιλογή των κατάλληλων ανεξάρτητων, εξαρτημένων και μεταβλητών ελέγχου, αλλά και το σχεδιασμό της διεξαγωγής του πειράματος υπό τις βέλτιστες στατιστικά συνθήκες, δεδομένων των περιορισμών των διαθέσιμων πόρων. Υπάρχουν πολλαπλές προσεγγίσεις για τον προσδιορισμό του συνόλου των σημείων σχεδιασμού (μοναδικοί συνδυασμοί των ρυθμίσεων των ανεξάρτητων μεταβλητών) που θα χρησιμοποιηθούν στο πείραμα.

Οι κύριες ανησυχίες στον πειραματικό σχεδιασμό περιλαμβάνουν τη διαπίστωση της εγκυρότητας, της αξιοπιστίας και της επαναληψιμότητας. Παραδείγματος χάριν, αυτές οι ανησυχίες μπορούν να αντιμετωπιστούν εν μέρει με την προσεκτική επιλογή της ανεξάρτητης μεταβλητής, τη μείωση του κινδύνου σφάλματος μέτρησης και τη διασφάλιση ότι η τεκμηρίωση της μεθόδου είναι επαρκώς λεπτομερής. Οι συναφείς ανησυχίες περιλαμβάνουν την επίτευξη κατάλληλων επιπέδων στατιστικής ισχύος και ευαισθησίας.

Τα σωστά σχεδιασμένα πειράματα προάγουν τη γνώση στις φυσικές και κοινωνικές επιστήμες και στη μηχανική, ενώ η μεθοδολογία σχεδιασμού πειραμάτων αναγνωρίζεται ως βασικό εργαλείο για την επιτυχή εφαρμογή ενός πλαισίου ποιότητας μέσω σχεδιασμού (QbD)[3]. Η μελέτη του σχεδιασμού πειραμάτων αποτελεί σημαντικό θέμα της μεταεπιστήμης.

Ιστορία

[Επεξεργασία | επεξεργασία κώδικα]

Στατιστικά πειράματα, σύμφωνα με τον Σαρλ Σ. Πιρς

[Επεξεργασία | επεξεργασία κώδικα]

Δείτε επίσης: Τυχαιοποίηση

Η θεωρία της στατιστικής συμπερασματολογίας αναπτύχθηκε από τον Σαρλ Σ. Πιρς στο "Illustrations of the Logic of Science" (Απεικονίσεις της επιστημονικής λογικής)(1877-1878)[4][5] και στο "A Theory of Probable Inference" (Μια θεωρία της πιθανής συμπερασματολογίας) (1883)[6], δύο δημοσιεύσεις που τόνισαν τη σημασία της συμπερασματολογίας στη στατιστική με βάση την τυχαιοποίηση[7].

Προσδιορισμένες δοκιμές

[Επεξεργασία | επεξεργασία κώδικα]

Ο Σαρλ Σ. Πιρς ανέθεσε τυχαία σε εθελοντές ένα τυφλό σχέδιο επαναλαμβανόμενων μετρήσεων για να αξιολογήσει την ικανότητά τους να διακρίνουν βάρη.[8][9][10][11] Το πείραμα του Πιρς ενέπνευσε άλλους ερευνητές στην ψυχολογία και την εκπαίδευση, οι οποίοι ανέπτυξαν μια ερευνητική παράδοση τυχαιοποιημένων πειραμάτων σε εργαστήρια και εξειδικευμένα εγχειρίδια τη δεκαετία του 1800.[8][9][10][11]

Βέλτιστοι σχεδιασμοί για μοντέλα παλινδρόμησης

[Επεξεργασία | επεξεργασία κώδικα]

Ο Σαρλ Σ. Πιρς συνεισέφερε επίσης την πρώτη αγγλόφωνη δημοσίευση σχετικά με έναν βέλτιστο σχεδιασμό για μοντέλα παλινδρόμησης το 1876[12] Ένας πρωτοποριακός βέλτιστος σχεδιασμός για πολυωνυμική παλινδρόμηση προτάθηκε από τον Γκεργκόν το 1815. Το 1918, η Κριστίν Σμιθ δημοσίευσε βέλτιστους σχεδιασμούς για πολυώνυμα έκτου (και μικρότερου) βαθμού[13][14]

Ακολουθίες πειραμάτων

[Επεξεργασία | επεξεργασία κώδικα]

Η χρήση μιας ακολουθίας πειραμάτων, όπου ο σχεδιασμός του καθενός μπορεί να εξαρτάται από τα αποτελέσματα των προηγούμενων πειραμάτων, συμπεριλαμβανομένης της πιθανής απόφασης να σταματήσει το πείραμα, εμπίπτει στο πεδίο της διαδοχικής ανάλυσης, ενός τομέα που πρωτοστάτησε[15] ο Αβραάμ Βαλντ στο πλαίσιο των διαδοχικών ελέγχων στατιστικών υποθέσεων.[16] Ο Χέρμαν Τσέρνοφ έγραψε μια επισκόπηση των βέλτιστων διαδοχικών σχεδιασμών[17], ενώ οι προσαρμοστικοί σχεδιασμοί έχουν εξεταστεί από τον Σ. Ζακς.[18] Ένας συγκεκριμένος τύπος διαδοχικού σχεδιασμού είναι η «δίχειρη ληστεία», γενικευμένη στην πολύχειρη ληστεία, πάνω στην οποία έγινε πρώιμη εργασία από τον Χέρμπερτ Ρόμπινς το 1952[19].

Αρχές του Φίσερ

[Επεξεργασία | επεξεργασία κώδικα]

Μια μεθοδολογία για το σχεδιασμό πειραμάτων προτάθηκε από τον Ρόναλντ Φίσερ, στα καινοτόμα βιβλία του: The Arrangement of Field Experiments (1926) και The Design of Experiments (Ο σχεδιασμός των πειραμάτων ) (1935). Μεγάλο μέρος του πρωτοποριακού του έργου αφορούσε τις γεωργικές εφαρμογές των στατιστικών μεθόδων. Ως πεζό παράδειγμα, περιέγραψε τον τρόπο δοκιμής της υπόθεσης "Lady tasting tea hypothesis" (Η κυρία δοκιμάζει την υπόθεση του τσαγιού), σύμφωνα με την οποία μια συγκεκριμένη κυρία μπορούσε να διακρίνει από τη γεύση και μόνο αν το γάλα ή το τσάι τοποθετήθηκε πρώτα στο φλιτζάνι. Οι μέθοδοι αυτές έχουν προσαρμοστεί ευρέως στη βιολογική, ψυχολογική και γεωργική έρευνα[20].

Σύγκριση

Σε ορισμένα επιστημονικά πεδία δεν είναι δυνατόν να υπάρχουν ανεξάρτητες μετρήσεις σε ένα ανιχνεύσιμο πρότυπο μετρολογίας. Οι συγκρίσεις μεταξύ των θεραπειών είναι πολύ πιο πολύτιμες και συνήθως προτιμώνται, και συχνά συγκρίνονται με έναν επιστημονικό έλεγχο ή μια παραδοσιακή θεραπεία που λειτουργεί ως γραμμή βάσης.

Τυχαιοποίηση

Τυχαία ανάθεση είναι η διαδικασία της τυχαίας ανάθεσης ατόμων σε ομάδες ή σε διαφορετικές ομάδες σε ένα πείραμα, έτσι ώστε κάθε άτομο του πληθυσμού να έχει την ίδια πιθανότητα να συμμετάσχει στη μελέτη. Η τυχαία ανάθεση των ατόμων σε ομάδες (ή συνθήκες εντός μιας ομάδας) διακρίνει ένα αυστηρό, "πραγματικό" πείραμα από μια μελέτη παρατήρησης ή ένα "οιονεί πείραμα"[21]. Υπάρχει ένα εκτεταμένο σώμα μαθηματικής θεωρίας που διερευνά τις συνέπειες της κατανομής των μονάδων σε θεραπείες μέσω κάποιου τυχαίου μηχανισμού (όπως πίνακες τυχαίων αριθμών ή η χρήση συσκευών τυχαιοποίησης όπως τα τραπουλόχαρτα ή τα ζάρια). Η τυχαία ανάθεση μονάδων σε θεραπείες τείνει να μετριάσει τη σύγχυση, η οποία κάνει τις επιδράσεις που οφείλονται σε παράγοντες άλλους από τη θεραπεία να εμφανίζονται ως αποτέλεσμα της θεραπείας.
Οι κίνδυνοι που συνδέονται με την τυχαία κατανομή (όπως η ύπαρξη σοβαρής ανισορροπίας σε ένα βασικό χαρακτηριστικό μεταξύ μιας ομάδας θεραπείας και μιας ομάδας ελέγχου) είναι υπολογίσιμοι και, ως εκ τούτου, μπορούν να αντιμετωπιστούν σε ένα αποδεκτό επίπεδο με τη χρήση αρκετών πειραματικών μονάδων. Ωστόσο, εάν ο πληθυσμός χωρίζεται σε διάφορους υποπληθυσμούς που διαφέρουν κατά κάποιο τρόπο και η έρευνα απαιτεί κάθε υποπληθυσμός να είναι ίσος σε μέγεθος, μπορεί να χρησιμοποιηθεί στρωματοποιημένη δειγματοληψία. Με αυτόν τον τρόπο, οι μονάδες σε κάθε υποπληθυσμό τυχαιοποιούνται, αλλά όχι ολόκληρο το δείγμα. Τα αποτελέσματα ενός πειράματος μπορούν να γενικευθούν αξιόπιστα από τις πειραματικές μονάδες σε έναν μεγαλύτερο στατιστικό πληθυσμό μονάδων μόνο εάν οι πειραματικές μονάδες αποτελούν τυχαίο δείγμα από τον μεγαλύτερο πληθυσμό- το πιθανό σφάλμα μιας τέτοιας παρέκτασης εξαρτάται, μεταξύ άλλων, από το μέγεθος του δείγματος.

Στατιστική επανάληψη

Οι μετρήσεις υπόκεινται συνήθως σε διακυμάνσεις και αβεβαιότητα μέτρησης- ως εκ τούτου, επαναλαμβάνονται και πλήρη πειράματα επαναλαμβάνονται για να βοηθήσουν στον εντοπισμό των πηγών της διακύμανσης, στην καλύτερη εκτίμηση των πραγματικών επιδράσεων των θεραπειών, στην περαιτέρω ενίσχυση της αξιοπιστίας και της εγκυρότητας του πειράματος και στην προσθήκη στην υπάρχουσα γνώση του θέματος.[22] Ωστόσο, πρέπει να πληρούνται ορισμένες προϋποθέσεις πριν από την έναρξη της αναπαραγωγής του πειράματος: το αρχικό ερευνητικό ερώτημα έχει δημοσιευθεί σε περιοδικό με κριτές ή έχει αναφερθεί ευρέως, ο ερευνητής είναι ανεξάρτητος από το αρχικό πείραμα, ο ερευνητής πρέπει πρώτα να προσπαθήσει να αναπαραγάγει τα αρχικά ευρήματα χρησιμοποιώντας τα αρχικά δεδομένα και η συγγραφή πρέπει να αναφέρει ότι η μελέτη που διεξήχθη είναι μια μελέτη αναπαραγωγής που προσπάθησε να ακολουθήσει όσο το δυνατόν πιο αυστηρά την αρχική μελέτη[23].

Αποκλεισμός

Αποκλεισμός (δεξιά)
Ο αποκλεισμός είναι η μη τυχαία διάταξη των πειραματικών μονάδων σε ομάδες (μπλοκ) που αποτελούνται από μονάδες που είναι παρόμοιες μεταξύ τους. Ο αποκλεισμός μειώνει τις γνωστές αλλά άσχετες πηγές διακύμανσης μεταξύ των μονάδων και επιτρέπει έτσι μεγαλύτερη ακρίβεια στην εκτίμηση της πηγής της υπό μελέτη διακύμανσης.

Ορθογωνιότητα

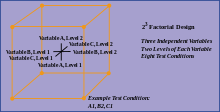
Παράδειγμα ορθογώνιου παραγοντικού σχεδιασμού
Η ορθογωνιότητα αφορά τις μορφές σύγκρισης (αντιθέσεις) που μπορούν να πραγματοποιηθούν νόμιμα και αποτελεσματικά. Οι αντιθέσεις μπορούν να αναπαρασταθούν με διανύσματα και τα σύνολα ορθογώνιων αντιθέσεων είναι ασυσχέτιστα και ανεξάρτητα κατανεμημένα εάν τα δεδομένα είναι κανονικά. Λόγω αυτής της ανεξαρτησίας, κάθε ορθογώνια επεξεργασία παρέχει διαφορετικές πληροφορίες από τις άλλες. Εάν υπάρχουν T θεραπείες και T-1 ορθογώνιες αντιθέσεις, όλες οι πληροφορίες που μπορούν να συλλεχθούν από το πείραμα μπορούν να ληφθούν από το σύνολο των αντιθέσεων.

Πολυπαραγοντικά πειράματα

Χρήση πολυπαραγοντικών πειραμάτων αντί της μεθόδου ενός παράγοντα κάθε φορά. Αυτά είναι αποτελεσματικά στην αξιολόγηση των επιδράσεων και των πιθανών αλληλεπιδράσεων πολλών παραγόντων (ανεξάρτητες μεταβλητές). Ο σχεδιασμός της ανάλυσης πειραμάτων βασίζεται στα θεμέλια της ανάλυσης διακύμανσης, μιας συλλογής μοντέλων που χωρίζουν την παρατηρούμενη διακύμανση σε συνιστώσες, ανάλογα με το ποιοι παράγοντες πρέπει να εκτιμηθούν ή να ελεγχθούν από το πείραμα.

Παράδειγμα

[Επεξεργασία | επεξεργασία κώδικα]

Αυτό το παράδειγμα πειραμάτων σχεδιασμού αποδίδεται στον Χάρολντ Χότελινγκ, βασιζόμενο σε παραδείγματα του Φρανκ Γέιτς.[24][25][17] Τα πειράματα που σχεδιάζονται σε αυτό το παράδειγμα περιλαμβάνουν συνδυαστικούς σχεδιασμούς[26].

Τα βάρη οκτώ αντικειμένων μετρώνται με τη χρήση μιας ζυγαριάς ταψιού και ενός συνόλου πρότυπων βαρών. Σε κάθε ζύγισμα μετράται η διαφορά βάρους μεταξύ των αντικειμένων που βρίσκονται στον αριστερό τηγάνι και τυχόν αντικειμένων που βρίσκονται στον δεξιό τηγάνι, προσθέτοντας βαθμονομημένα βάρη στον ελαφρύτερο τηγάνι μέχρι η ζυγαριά να ισορροπήσει. Κάθε μέτρηση έχει ένα τυχαίο σφάλμα. Το μέσο σφάλμα είναι μηδέν- οι τυπικές αποκλίσεις της κατανομής πιθανότητας των σφαλμάτων είναι ο ίδιος αριθμός σ σε διαφορετικές ζυγίσεις- τα σφάλματα σε διαφορετικές ζυγίσεις είναι ανεξάρτητα. Συμβολίζουμε τα πραγματικά βάρη με

Εξετάζουμε δύο διαφορετικά πειράματα:

  1. Ζυγίζουμε κάθε αντικείμενο σε ένα ταψί, με το άλλο ταψί άδειο. Έστω 'Xi το μετρούμενο βάρος του αντικειμένου, για i = 1, ..., 8.
  2. Τα οκτώ ζυγίσματα πραγματοποιούνται σύμφωνα με το ακόλουθο πρόγραμμα - έναν πίνακα ζυγίσεων:

Έστω Yi η μετρούμενη διαφορά για i = 1, ..., 8. Τότε η εκτιμώμενη τιμή του βάρους θ1 είναι

Παρόμοιες εκτιμήσεις μπορούν να βρεθούν και για τα βάρη των άλλων στοιχείων:

Το ερώτημα του σχεδιασμού των πειραμάτων είναι: ποιο πείραμα είναι καλύτερο;

Η διακύμανση της εκτίμησης X1 του θ1 είναι σ2 αν χρησιμοποιήσουμε το πρώτο πείραμα. Αν όμως χρησιμοποιήσουμε το δεύτερο πείραμα, η διακύμανση της παραπάνω εκτίμησης είναι 'σ2/8. Έτσι, το δεύτερο πείραμα μας δίνει 8 φορές μεγαλύτερη ακρίβεια για την εκτίμηση ενός μόνο στοιχείου και εκτιμά όλα τα στοιχεία ταυτόχρονα, με την ίδια ακρίβεια. Αυτό που επιτυγχάνει το δεύτερο πείραμα με οκτώ θα απαιτούσε 64 ζυγίσματα, αν τα αντικείμενα ζυγίζονταν ξεχωριστά. Ωστόσο, σημειώστε ότι οι εκτιμήσεις για τα αντικείμενα που λαμβάνονται στο δεύτερο πείραμα έχουν σφάλματα που συσχετίζονται μεταξύ τους.

Πολλά προβλήματα σχεδιασμού πειραμάτων περιλαμβάνουν συνδυαστικούς σχεδιασμούς, όπως σε αυτό το παράδειγμα και σε άλλα[26].

Αποφυγή ψευδώς θετικών αποτελεσμάτων

[Επεξεργασία | επεξεργασία κώδικα]

Δείτε επίσης: Μετα-έρευνα

Τα λανθασμένα θεωρητικά συμπεράσματα, που συχνά προκύπτουν από την πίεση για δημοσίευση ή από την προκατάληψη επιβεβαίωσης του ίδιου του συγγραφέα, αποτελούν εγγενή κίνδυνο σε πολλούς τομείς[27].

Η χρήση από διπλές τυφλές μελέτες μπορεί να αποτρέψει τις προκαταλήψεις που ενδέχεται να οδηγήσουν σε ψευδώς θετικά αποτελέσματα στη φάση της συλλογής δεδομένων. Όταν χρησιμοποιείται ένας διπλά τυφλός σχεδιασμός, οι συμμετέχοντες κατανέμονται τυχαία σε πειραματικές ομάδες, αλλά ο ερευνητής δεν γνωρίζει ποιοι συμμετέχοντες ανήκουν σε ποια ομάδα. Ως εκ τούτου, ο ερευνητής δεν μπορεί να επηρεάσει την ανταπόκριση των συμμετεχόντων στην παρέμβαση[28].

Οι πειραματικοί σχεδιασμοί με μη αποκαλυπτόμενους βαθμούς ελευθερίας[αργκό] αποτελούν πρόβλημα,[29] καθώς μπορούν να οδηγήσουν σε συνειδητό ή ασυνείδητο "p-hacking": να δοκιμάζεις πολλά πράγματα μέχρι να έχεις το επιθυμητό αποτέλεσμα. Συνήθως περιλαμβάνει τον χειρισμό - ίσως ασυνείδητα - της διαδικασίας της στατιστικής ανάλυσης και των βαθμών ελευθερίας μέχρι να επιστρέψουν ένα ποσοστό κάτω από το επίπεδο στατιστικής σημαντικότητας p<.05[30][31] .

Το P-hacking μπορεί να αποτραπεί με την προεγγραφή των ερευνών, κατά την οποία οι ερευνητές πρέπει να στείλουν το σχέδιο ανάλυσης των δεδομένων τους στο περιοδικό στο οποίο επιθυμούν να δημοσιεύσουν τη δημοσίευσή τους πριν καν ξεκινήσουν τη συλλογή δεδομένων, ώστε να μην είναι δυνατή η χειραγώγηση των δεδομένων[32][33].

Ένας άλλος τρόπος για να αποφευχθεί αυτό είναι η λήψη ενός διπλά τυφλού σχεδίου στη φάση της ανάλυσης δεδομένων, καθιστώντας τη μελέτη τριπλά τυφλή, όπου τα δεδομένα αποστέλλονται σε έναν αναλυτή δεδομένων που δεν σχετίζεται με την έρευνα, ο οποίος ανακατεύει τα δεδομένα, ώστε να μην υπάρχει τρόπος να γνωρίζουμε σε ποιους ανήκουν οι συμμετέχοντες πριν ενδεχομένως απομακρυνθούν ως ακραίοι[28].

Η σαφής και πλήρης τεκμηρίωση της πειραματικής μεθοδολογίας είναι επίσης σημαντική προκειμένου να υποστηριχθεί η αναπαραγωγή των αποτελεσμάτων[34].

Θέματα συζήτησης κατά τη δημιουργία ενός πειραματικού σχεδίου

[Επεξεργασία | επεξεργασία κώδικα]

Ένας πειραματικός σχεδιασμός ή μια τυχαιοποιημένη κλινική δοκιμή απαιτεί την προσεκτική εξέταση διαφόρων παραγόντων πριν από την πραγματοποίηση του πειράματος.[35] Ένας πειραματικός σχεδιασμός είναι η εκπόνηση ενός λεπτομερούς πειραματικού σχεδίου πριν από την πραγματοποίηση του πειράματος. Ορισμένα από τα ακόλουθα θέματα έχουν ήδη συζητηθεί στην ενότητα "Αρχές πειραματικού σχεδιασμού":

  1. Πόσους παράγοντες έχει ο σχεδιασμός και είναι τα επίπεδα αυτών των παραγόντων σταθερά ή τυχαία;
  2. Χρειάζονται συνθήκες ελέγχου και ποιες πρέπει να είναι αυτές;
  3. Έλεγχοι χειραγώγησης: λειτούργησε πραγματικά η χειραγώγηση;
  4. Ποιες είναι οι μεταβλητές υποβάθρου;
  5. Ποιο είναι το μέγεθος του δείγματος; Πόσες μονάδες πρέπει να συλλεχθούν ώστε το πείραμα να είναι γενικεύσιμο και να έχει αρκετή ισχύ;
  6. Ποια είναι η σημασία των αλληλεπιδράσεων μεταξύ των παραγόντων;
  7. Ποια είναι η επιρροή των καθυστερημένων επιδράσεων των ουσιαστικών παραγόντων στα αποτελέσματα;
  8. Πώς επηρεάζουν οι μετατοπίσεις της απόκρισης τις μετρήσεις αυτοαναφοράς;
  9. Πόσο εφικτή είναι η επαναλαμβανόμενη χορήγηση των ίδιων οργάνων μέτρησης στις ίδιες μονάδες σε διαφορετικές περιστάσεις, με ένα post-test και δοκιμές παρακολούθησης;
  10. Τι γίνεται με τη χρήση ενός προ-τεστ με πληρεξούσιο;
  11. Υπάρχουν συγχυτικές μεταβλητές;
  12. Θα πρέπει ο πελάτης/ασθενής, ο ερευνητής ή ακόμη και ο αναλυτής των δεδομένων να είναι τυφλοί ως προς τις συνθήκες;
  13. Ποια είναι η δυνατότητα μεταγενέστερης εφαρμογής διαφορετικών συνθηκών στις ίδιες μονάδες;
  14. Πόσοι από κάθε παράγοντα ελέγχου και θορύβου πρέπει να λαμβάνονται υπόψη;

Η ανεξάρτητη μεταβλητή μιας μελέτης συγκεντρώνει συχνά πολλά επίπεδα ή διαφορετικές ομάδες. Σε ένα πραγματικό πείραμα, οι ερευνητές μπορούν να έχουν μια πειραματική ομάδα, στην οποία εφαρμόζεται η παρέμβασή τους που ελέγχει την υπόθεση, και μια ομάδα ελέγχου, η οποία έχει όλα τα ίδια στοιχεία με την πειραματική ομάδα, χωρίς το παρεμβατικό στοιχείο. Επομένως, όταν όλα τα υπόλοιπα εκτός από μια παρέμβαση παραμένουν σταθερά, οι ερευνητές μπορούν να πιστοποιήσουν με κάποια βεβαιότητα ότι αυτό το ένα στοιχείο είναι αυτό που προκάλεσε την παρατηρούμενη αλλαγή. Σε ορισμένες περιπτώσεις, η ύπαρξη ομάδας ελέγχου δεν είναι δεοντολογική. Αυτό μερικές φορές επιλύεται με τη χρήση δύο διαφορετικών πειραματικών ομάδων. Σε ορισμένες περιπτώσεις, οι ανεξάρτητες μεταβλητές δεν μπορούν να χειραγωγηθούν, για παράδειγμα όταν ελέγχεται η διαφορά μεταξύ δύο ομάδων που πάσχουν από διαφορετική ασθένεια ή όταν ελέγχεται η διαφορά μεταξύ των φύλων (προφανώς μεταβλητές στις οποίες θα ήταν δύσκολο ή ανήθικο να ανατεθούν οι συμμετέχοντες). Σε αυτές τις περιπτώσεις, μπορεί να χρησιμοποιηθεί ένας οιονεί πειραματικός σχεδιασμός.

Αιτιολογία

[Επεξεργασία | επεξεργασία κώδικα]

Στον αμιγώς πειραματικό σχεδιασμό, η ανεξάρτητη (προβλεπτική) μεταβλητή χειραγωγείται από τον ερευνητή - δηλαδή - κάθε συμμετέχων στην έρευνα επιλέγεται τυχαία από τον πληθυσμό, και κάθε συμμετέχων που επιλέγεται ανατίθεται τυχαία σε συνθήκες της ανεξάρτητης μεταβλητής. Μόνο όταν γίνει αυτό είναι δυνατόν να πιστοποιηθεί με μεγάλη πιθανότητα ότι ο λόγος των διαφορών στις μεταβλητές αποτελέσματος οφείλεται στις διαφορετικές συνθήκες. Ως εκ τούτου, οι ερευνητές πρέπει να επιλέγουν τον πειραματικό σχεδιασμό έναντι άλλων τύπων σχεδιασμού όποτε είναι δυνατόν. Ωστόσο, η φύση της ανεξάρτητης μεταβλητής δεν επιτρέπει πάντοτε τη χειραγώγηση. Σε αυτές τις περιπτώσεις, οι ερευνητές πρέπει να γνωρίζουν ότι δεν πρέπει να πιστοποιούν σχετικά με την αιτιώδη απόδοση όταν ο σχεδιασμός τους δεν το επιτρέπει. Επί παραδείγματι, στους σχεδιασμούς παρατήρησης, οι συμμετέχοντες δεν κατανέμονται τυχαία στις συνθήκες και, επομένως, εάν διαπιστωθούν διαφορές στις μεταβλητές έκβασης μεταξύ των συνθηκών, είναι πιθανό να υπάρχει κάτι άλλο εκτός από τις διαφορές μεταξύ των συνθηκών που προκαλεί τις διαφορές στα αποτελέσματα, δηλαδή - μια τρίτη μεταβλητή. Το ίδιο ισχύει και για τις μελέτες με συσχετιστικό σχεδιασμό.

Στατιστικός έλεγχος

[Επεξεργασία | επεξεργασία κώδικα]

Είναι προτιμότερο μια διαδικασία να βρίσκεται σε λογικό στατιστικό έλεγχο πριν από τη διεξαγωγή σχεδιασμένων πειραμάτων. Όταν αυτό δεν είναι εφικτό, ο κατάλληλος αποκλεισμός, η επανάληψη και η τυχαιοποίηση επιτρέπουν την προσεκτική διεξαγωγή σχεδιασμένων πειραμάτων[36]. Οι ερευνητές πρέπει να διασφαλίζουν ότι οι μη ελεγχόμενες επιρροές (π.χ. αντίληψη της αξιοπιστίας της πηγής) δεν αλλοιώνουν τα ευρήματα της μελέτης. Ο έλεγχος χειραγώγησης είναι ένα παράδειγμα ελέγχου ελέγχου. Οι έλεγχοι χειραγώγησης επιτρέπουν στους ερευνητές να απομονώσουν τις κύριες μεταβλητές για να ενισχύσουν την υποστήριξη ότι οι μεταβλητές αυτές λειτουργούν όπως προβλέπεται.

Μία από τις σημαντικότερες απαιτήσεις των πειραματικών ερευνητικών σχεδίων είναι η ανάγκη εξάλειψης των επιδράσεων των ψευδών, παρεμβατικών και προγενέστερων μεταβλητών. Στο πιο βασικό μοντέλο, η αιτία (Χ) οδηγεί στο αποτέλεσμα (Υ). Θα μπορούσε όμως να υπάρχει μια τρίτη μεταβλητή (Ζ) που επηρεάζει την (Υ) και η Χ μπορεί να μην είναι καθόλου η πραγματική αιτία. Η Ζ λέγεται ψευδομεταβλητή και πρέπει να ελέγχεται. Το ίδιο ισχύει και για τις παρεμβατικές μεταβλητές (μια μεταβλητή που βρίσκεται μεταξύ της υποτιθέμενης αιτίας (Χ) και του αποτελέσματος (Υ)) και τις προγενέστερες μεταβλητές (μια μεταβλητή πριν από την υποτιθέμενη αιτία (Χ) που είναι η πραγματική αιτία). Όταν εμπλέκεται μια τρίτη μεταβλητή και δεν έχει ελεγχθεί, η σχέση λέγεται ότι είναι σχέση μηδενικής τάξης. Στις περισσότερες πρακτικές εφαρμογές πειραματικών ερευνητικών σχεδίων υπάρχουν πολλές αιτίες (Χ1, Χ2, Χ3). Στα περισσότερα σχέδια, μόνο μία από αυτές τις αιτίες χειραγωγείται κάθε φορά.

Πειραματικοί σχεδιασμοί μετά τον Φίσερ

[Επεξεργασία | επεξεργασία κώδικα]

Ορισμένοι αποτελεσματικοί σχεδιασμοί για την εκτίμηση πολλών κύριων επιδράσεων βρέθηκαν ανεξάρτητα και σχεδόν διαδοχικά από τους Ρατζ Τσάντρα Μπόσε και Κ. Κισέν το 1940 στο Ινδικό Στατιστικό Ινστιτούτο, αλλά παρέμειναν ελάχιστα γνωστοί μέχρι τη δημοσίευση των σχεδιασμών Πλάκετ-Μπέρμαν στο περιοδικό Biometrika το 1946. Περίπου την ίδια εποχή, ο Κ. Ρ. Ράο εισήγαγε τις έννοιες των ορθογώνιων συστοιχιών ως πειραματικών σχεδίων. Η έννοια αυτή έπαιξε κεντρικό ρόλο στην ανάπτυξη των μεθόδων Ταγκούτσι από τον Γκενίτσι Ταγκούτσι, η οποία έλαβε χώρα κατά την επίσκεψή του στο Ινδικό Στατιστικό Ινστιτούτο στις αρχές της δεκαετίας του 1950. Οι μέθοδοί του εφαρμόστηκαν και υιοθετήθηκαν με επιτυχία από τις ιαπωνικές και ινδικές βιομηχανίες και στη συνέχεια αγκαλιάστηκαν επίσης από τη βιομηχανία των ΗΠΑ, αν και με ορισμένες επιφυλάξεις.

Το 1950, η Γκέρτρουντ Μαίρη Κοξ και ο Γουίλιαμ Τζέμελ Κόχραν δημοσίευσαν το βιβλίο Experimental Designs, το οποίο αποτέλεσε το σημαντικότερο έργο αναφοράς για το σχεδιασμό πειραμάτων για τους στατιστικολόγους για χρόνια μετά.

Οι εξελίξεις της θεωρίας των γραμμικών μοντέλων περιέλαβαν και ξεπέρασαν τις περιπτώσεις που απασχόλησαν τους πρώτους συγγραφείς. Σήμερα, η θεωρία στηρίζεται σε προηγμένα θέματα γραμμικής άλγεβρας, άλγεβρας και συνδυαστικής.

Όπως και σε άλλους κλάδους της στατιστικής, ο πειραματικός σχεδιασμός επιδιώκεται με τη χρήση τόσο συχνιστικών όσο και Μπεϋζιανών προσεγγίσεων: Κατά την αξιολόγηση στατιστικών διαδικασιών όπως οι πειραματικοί σχεδιασμοί, η συχνιστική στατιστική μελετά τη δειγματοληπτική κατανομή, ενώ η Μπεϋζιανή στατιστική ενημερώνει μια κατανομή πιθανότητας στο χώρο των παραμέτρων.

Ορισμένοι σημαντικοί συνεισφέροντες στον τομέα των πειραματικών σχεδιασμών είναι οι C. S. Πιρς, R. A. Φίσερ, F. Γέιτς, R. C. Μπόουζ, A. C. Άτκινσον, R. A. Μπέιλι, D. R. Κοξ, G. E. P. Box, W. G. Κόχραν, W. T. Φέντερερ, V. V. Φεντορόφ, A. S. Χενταγιάτ, J. Κίφερ, Ο. Κέμπθορν, J. Α. Νέλντερ, Αντρέι Πάζμαν, Φρίντριχ Πουκελσχάιμ, D. Ραγκαβάραο, Κ. Ρ. Ράο, Σρικχάντε Σ. Σ, J. N. Σριβαστάνα, Γουίλιαμ J. Στάντεν, G. Ταγκούσι και H. P. Γκουιν[37].

Τα εγχειρίδια των Ν. Μοντγκόμερι, Ρ. Μάγιερς και Γ. Μποξ/Γου. Χάντερ/J.S. Χάντερ έχουν φτάσει σε γενιές φοιτητών και επαγγελματιών[38][39][40][41][42]. Επιπλέον, υπάρχει συνεχής συζήτηση για τον πειραματικό σχεδιασμό στο πλαίσιο της κατασκευής μοντέλων για μοντέλα είτε στατικά είτε δυναμικά μοντέλα, γνωστά και ως ταυτοποίηση συστήματος.[43][44]

Περιορισμοί ανθρώπινων συμμετεχόντων

[Επεξεργασία | επεξεργασία κώδικα]

Οι νόμοι και οι δεοντολογικοί λόγοι αποκλείουν ορισμένα προσεκτικά σχεδιασμένα πειράματα με ανθρώπινα υποκείμενα. Οι νομικοί περιορισμοί εξαρτώνται από τη δικαιοδοσία. Οι περιορισμοί μπορεί να περιλαμβάνουν επιτροπές αξιολόγησης ιδρυμάτων, συγκατάθεση μετά από ενημέρωση και εμπιστευτικότητα που επηρεάζουν τόσο τις κλινικές (ιατρικές) δοκιμές όσο και τα πειράματα συμπεριφοράς και κοινωνικών επιστημών.[45] Στον τομέα της τοξικολογίας, για παράδειγμα, πραγματοποιούνται πειράματα σε πειραματόζωα με στόχο τον καθορισμό ασφαλών ορίων έκθεσης για τον άνθρωπο.[46] Οι περιορισμοί εξισορροπούνται με απόψεις από τον ιατρικό τομέα.[47] Όσον αφορά την τυχαιοποίηση των ασθενών, "... αν κανείς δεν γνωρίζει ποια θεραπεία είναι καλύτερη, δεν υπάρχει ηθική επιταγή να χρησιμοποιηθεί η μία ή η άλλη θεραπεία". (σελ. 380) Όσον αφορά τον πειραματικό σχεδιασμό, "...είναι σαφώς μη ηθικό να θέτουμε τα υποκείμενα σε κίνδυνο για τη συλλογή δεδομένων σε μια κακοσχεδιασμένη μελέτη, όταν η κατάσταση αυτή μπορεί εύκολα να αποφευχθεί...". (p 393)

Εξωτερικοί σύνδεσμοι

[Επεξεργασία | επεξεργασία κώδικα]

Δείτε επίσης

[Επεξεργασία | επεξεργασία κώδικα]

Βιβλιογραφία

[Επεξεργασία | επεξεργασία κώδικα]

Παραπομπές

[Επεξεργασία | επεξεργασία κώδικα]
  1. ↑ «What Is Design of Experiments (DOE)?». asq.org. American Society for Quality. Ανακτήθηκε στις 20 Φεβρουαρίου 2025. 
  2. ↑ «What are Variables?». Science Buddies (στα Αγγλικά). Ανακτήθηκε στις 24 Φεβρουαρίου 2025. 
  3. ↑ «The Sequential Nature of Classical Design of Experiments | Prism». prismtc.co.uk. Ανακτήθηκε στις 10 Μαρτίου 2023. 
  4. ↑ Peirce, Charles Sanders (1887). "Illustrations of the Logic of Science". Open Court (10 June 2014). ISBN 0812698495.
  5. ↑ «Popular Science Monthly/Volume 12/January 1878/Illustrations of the Logic of Science II - Wikisource, the free online library». en.wikisource.org (στα Αγγλικά). Ανακτήθηκε στις 24 Φεβρουαρίου 2025. 
  6. ↑ Peirce, Charles Sanders (1883). "A Theory of Probable Inference". In C. S. Peirce (Ed.), Studies in logic by members of the Johns Hopkins University (p. 126–181). Little, Brown and Co (1883)
  7. ↑ Stigler, Stephen M. (1978). «Mathematical statistics in the early States». Annals of Statistics 6 (2): 239–65 [248]. doi:10.1214/aos/1176344123.
    MR 483118
    . http://projecteuclid.org/euclid.aos/1176344123. «"Indeed, Pierce's work contains one of the earliest explicit endorsements of mathematical randomization as a basis for inference of which I am aware (Peirce, 1957, pages 216–219"».     
  8. ↑ 8,0 8,1 Peirce, Charles Sanders; Jastrow, Joseph (1885). «On Small Differences in Sensation». Memoirs of the National Academy of Sciences 3: 73–83. http://psychclassics.yorku.ca/Peirce/small-diffs.htm. 
  9. ↑ 9,0 9,1 of Hacking, Ian (September 1988). «Telepathy: Origins of Randomization in Experimental Design». Isis 79 (3): 427–451. doi:10.1086/354775.
    MR 1013489
    .     
  10. ↑ 10,0 10,1 Stephen M. Stigler (November 1992). «A Historical View of Statistical Concepts in Psychology and Educational Research». American Journal of Education 101 (1): 60–70. doi:10.1086/444032. 
  11. ↑ 11,0 11,1 Trudy Dehue (December 1997). «Deception, Efficiency, and Random Groups: Psychology and the Gradual Origination of the Random Group Design». Isis 88 (4): 653–673. doi:10.1086/383850. PMID 9519574. https://www.rug.nl/research/portal/en/publications/deception-efficiency-and-random-groups(459e54f0-1e56-4390-876a-46a33e80621d).html. 
  12. ↑ Peirce, C. S. (1876). «Note on the Theory of the Economy of Research». Coast Survey Report: 197–201. , actually published 1879, NOAA PDF Eprint Αρχειοθετήθηκε 2 March 2017 στο Wayback Machine..
    Reprinted in Collected Papers 7, paragraphs 139–157, also in Writings 4, pp. 72–78, and in Peirce, C. S. (July–August 1967). «Note on the Theory of the Economy of Research». Operations Research 15 (4): 643–648. doi:10.1287/opre.15.4.643. 
  13. ↑ Guttorp, P.; Lindgren, G. (2009). «Karl Pearson and the Scandinavian school of statistics». International Statistical Review 77: 64. doi:10.1111/j.1751-5823.2009.00069.x. 
  14. ↑ Smith, Kirstine (1918). «On the standard deviations of adjusted and interpolated values of an observed polynomial function and its constants and the guidance they give towards a proper choice of the distribution of observations.». Biometrika 12 (1–2): 1–85. doi:10.1093/biomet/12.1-2.1. https://books.google.com/books?id=UMNLAAAAYAAJ. 
  15. ↑ Johnson, N.L. (1961). "Sequential analysis: a survey." Journal of the Royal Statistical Society, Series A. Vol. 124 (3), 372–411. (pages 375–376)
  16. ↑ Wald, A. (1945) "Sequential Tests of Statistical Hypotheses", Annals of Mathematical Statistics, 16 (2), 117–186.
  17. ↑ 17,0 17,1 Herman Chernoff, Sequential Analysis and Optimal Design, SIAM Monograph, 1972.
  18. ↑ Zacks, S. (1996) "Adaptive Designs for Parametric Models". In: Ghosh, S. and Rao, C. R., (Eds) (1996). "Design and Analysis of Experiments," Handbook of Statistics, Volume 13. North-Holland. ISBN 0-444-82061-2. (pages 151–180)
  19. ↑ Robbins, H. (1952). «Some Aspects of the Sequential Design of Experiments». Bulletin of the American Mathematical Society 58 (5): 527–535. doi:10.1090/S0002-9904-1952-09620-8. 
  20. ↑ Miller, Geoffrey (2000). The Mating Mind: how sexual choice shaped the evolution of human nature, London: Heineman, ISBN 0-434-00741-2 (also Doubleday, ISBN 0-385-49516-1) "To biologists, he was an architect of the 'modern synthesis' that used mathematical models to integrate Mendelian genetics with Darwin's selection theories. To psychologists, Fisher was the inventor of various statistical tests that are still supposed to be used whenever possible in psychology journals. To farmers, Fisher was the founder of experimental agricultural research, saving millions from starvation through rational crop breeding programs." p.54.
  21. ↑ Creswell, J.W. (2008), Educational research: Planning, conducting, and evaluating quantitative and qualitative research (3rd edition), Upper Saddle River, NJ: Prentice Hall. 2008, p. 300. ISBN 0-13-613550-1
  22. ↑ Dr. Hani (2009). «Replication study». Αρχειοθετήθηκε από το πρωτότυπο στις 2 Ιουνίου 2012. Ανακτήθηκε στις 27 Οκτωβρίου 2011. 
  23. ↑ Burman, Leonard E.; Robert W. Reed; James Alm (2010), «A call for replication studies», Public Finance Review 38 (6): 787–793, doi:10.1177/1091142110385210, http://pfr.sagepub.com, ανακτήθηκε στις 27 October 2011 
  24. ↑ Hotelling, Harold (1944). «Some Improvements in Weighing and Other Experimental Techniques». Annals of Mathematical Statistics 15 (3): 297–306. doi:10.1214/aoms/1177731236. https://projecteuclid.org/euclid.aoms/1177731236. 
  25. ↑ Giri, Narayan C.· Das, M. N. (1979). Design and Analysis of Experiments. New York, N.Y: Wiley. σελίδες 350–359. ISBN 9780852269145. 
  26. ↑ 26,0 26,1 Jack Sifri (8 Δεκεμβρίου 2014). «How to Use Design of Experiments to Create Robust Designs With High Yield». youtube.com. Ανακτήθηκε στις 11 Φεβρουαρίου 2015. 
  27. ↑ Forstmeier, Wolfgang; Wagenmakers, Eric-Jan; Parker, Timothy H. (23 November 2016). «Detecting and avoiding likely false-positive findings – a practical guide» (στα αγγλικά). Biological Reviews 92 (4): 1941–1968. doi:10.1111/brv.12315. ISSN 1464-7931. PMID 27879038. 
  28. ↑ 28,0 28,1 David, Sharoon; Khandhar1, Paras B. (July 17, 2023). «Double-Blind Study». StatPearls Publishing. PMID 31536248. https://www.ncbi.nlm.nih.gov/books/NBK546641/. 
  29. ↑ Simmons, Joseph; Leif Nelson; Uri Simonsohn (November 2011). «False-Positive Psychology: Undisclosed Flexibility in Data Collection and Analysis Allows Presenting Anything as Significant». Psychological Science 22 (11): 1359–1366. doi:10.1177/0956797611417632. ISSN 0956-7976. PMID 22006061. 
  30. ↑ «Science, Trust And Psychology in Crisis». KPLU. 2014-06-02. Αρχειοθετήθηκε από το πρωτότυπο στις 14 July 2014. https://web.archive.org/web/20140714151939/http://www.kplu.org/post/science-trust-and-psychology-crisis. Ανακτήθηκε στις 2014-06-12. 
  31. ↑ «Why Statistically Significant Studies Can Be Insignificant». Pacific Standard. 2014-06-04. https://psmag.com/environment/statistically-significant-studies-arent-necessarily-significant-82832. Ανακτήθηκε στις 2014-06-12. 
  32. ↑ Nosek, Brian A.; Ebersole, Charles R.; DeHaven, Alexander C.; Mellor, David T. (2018-03-13). «The preregistration revolution» (στα αγγλικά). Proceedings of the National Academy of Sciences 115 (11): 2600–2606. doi:10.1073/pnas.1708274114. ISSN 0027-8424. PMID 29531091. Bibcode: 2018PNAS..115.2600N. 
  33. ↑ «Pre-Registering Studies – What Is It, How Do You Do It, and Why?». www.acf.hhs.gov (στα Αγγλικά). Ανακτήθηκε στις 29 Αυγούστου 2023. 
  34. ↑ Chris Chambers (2014-06-10). «Physics envy: Do 'hard' sciences hold the solution to the replication crisis in psychology?». theguardian.com. https://www.theguardian.com/science/head-quarters/2014/jun/10/physics-envy-do-hard-sciences-hold-the-solution-to-the-replication-crisis-in-psychology. Ανακτήθηκε στις 2014-06-12. 
  35. ↑ Ader, Mellenberg & Hand (2008) "Advising on Research Methods: A consultant's companion"
  36. ↑ Bisgaard, S (2008) "Must a Process be in Statistical Control before Conducting Designed Experiments?", Quality Engineering, ASQ, 20 (2), pp 143–176
  37. ↑ Giri, Narayan C.· Das, M. N. (1979). Design and Analysis of Experiments. New York, N.Y: Wiley. σελίδες 53, 159, 264. ISBN 9780852269145. 
  38. ↑ Montgomery, Douglas (2013). Design and analysis of experiments (8th έκδοση). Hoboken, NJ: John Wiley & Sons, Inc. ISBN 9781118146927. 
  39. ↑ Walpole, Ronald E.· Myers, Raymond H.· Myers, Sharon L.· Ye, Keying (2007). Probability & statistics for engineers & scientists (8 έκδοση). Upper Saddle River, NJ: Pearson Prentice Hall. ISBN 978-0131877115. 
  40. ↑ Myers, Raymond H.· Montgomery, Douglas C.· Vining, G. Geoffrey· Robinson, Timothy J. (2010). Generalized linear models : with applications in engineering and the sciences (2 έκδοση). Hoboken, N.J.: Wiley. ISBN 978-0470454633. 
  41. ↑ Box, George E.P.· Hunter, William G.· Hunter, J. Stuart (1978). Statistics for Experimenters : An Introduction to Design, Data Analysis, and Model Building. New York: Wiley. ISBN 978-0-471-09315-2. 
  42. ↑ Box, George E.P.· Hunter, William G.· Hunter, J. Stuart (2005). Statistics for Experimenters : Design, Innovation, and Discovery (2 έκδοση). Hoboken, N.J.: Wiley. ISBN 978-0471718130. 
  43. ↑ Spall, J. C. (2010). «Factorial Design for Efficient Experimentation: Generating Informative Data for System Identification». IEEE Control Systems Magazine 30 (5): 38–53. doi:10.1109/MCS.2010.937677. 
  44. ↑ Pronzato, L (2008). «Optimal experimental design and some related control problems». Automatica 44 (2): 303–325. doi:10.1016/j.automatica.2007.05.016. 
  45. ↑ Moore, David S.· Notz, William I. (2006). Statistics : concepts and controversies (6th έκδοση). New York: W.H. Freeman. σελίδες Chapter 7: Data ethics. ISBN 9780716786368. 
  46. ↑ Ottoboni, M. Alice (1991). The dose makes the poison : a plain-language guide to toxicology (2nd έκδοση). New York, N.Y: Van Nostrand Reinhold. ISBN 978-0442006600. 
  47. ↑ Glantz, Stanton A. (1992). Primer of biostatistics (3rd έκδοση). ISBN 978-0-07-023511-3. 

Πηγές

[Επεξεργασία | επεξεργασία κώδικα]
Ανακτήθηκε από "https://el.wikipedia.org/w/index.php?title=Πειραματικός_σχεδιασμός&oldid=11005180"