Συζήτηση:Φωνόνιο
| Αυτό το λήμμα είναι στο πλαίσιο ενδιαφέροντος της «Βικιεπιχείρησης Φυσικές Επιστήμες», μια προσπάθεια για την βελτίωση και εμπλουτισμό της Βικιπαίδειας με λήμματα που αφορούν αυτό τον τομέα. Για να συμμετάσχετε και εσείς στη Βικιεπιχείρηση, επισκεφτείτε τη σχετική σελίδα όπου μπορείτε να συμμετάσχετε στη συζήτηση και να δείτε ανοιχτά ζητήματα για εργασία. | |
| Αυτό το λήμμα αποτιμήθηκε ως τάξης Προς επέκταση κατά την κλίμακα ποιότητας. | |
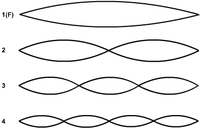
Τα modes of vibration είναι πολύ συγκεκριμένο πράγμα, βλέπε σχήμα με τα 4 πρώτα modes ταλάντωσης δοκού ακίνητου στα 2 άκρα. Τα "modes" δεν νομίζω ότι μεταφράζονται "τρόποι".--vanakaris 11:08, 21 Ιανουαρίου 2009 (UTC)
Στη Φυσική Στερεάς Βαρώτσου-Αλεξόπουλου (Σαβάλας 1995) αποδίδονται ακριβώς ως κανονικοί τρόποι ταλάντωσης. Και όχι μόνο εκεί βέβαια - Badseed απάντηση 11:15, 21 Ιανουαρίου 2009 (UTC)
- A ok τότε, δεν το'ξερα ότι έχει μεταφραστεί έτσι από Βαρώτσο-Αλεξόπουλο.--vanakaris 12:08, 21 Ιανουαρίου 2009 (UTC)
Χμμ, τα στάσιμα κύματα δε μεταφέρουν ενέργεια πέραν των άκρων που ορίζουν την ταλάντωσή τους. Ένα φωνόνιο σίγουρα μεταφέρει ενέργεια όπως ένα οδεύον κύμα και η περιγραφή του ως στάσιμο κύμα αρχικά με μπέρδεψε. Παρόλα αυτά ενδέχεται κάποιος πονηρός να υποβοηθείται μαθηματικά χρησιμοποιώντας μοντέλο φωνονίου ως στάσιμο κύμα που φέρει ενέργεια και είναι παγιδευμένο μέσα σε ένα "μπαλάκι" (διαστάσεων συγκρίσιμων των αποστάσεων των ατόμων στο κρυσταλλικό πλέγμα και εξαρτώμενων της φύσης και της γεωμετρίας του πλέγματος) που ταξιδεύει με μηδενική σπατάλη ενέργειας. Η απόδοση ως στάσιμο κύμα διαισθητικά με φέρνει πιο κοντά στη σωματιδιακή φύση του φωνονίου παρά στην κυματική του! Προσοχή πάντως, εύκολα το πιάνει στραβά κανείς. Άντε να δούμε πώς θα το μεταφέρουμε στο λήμμα. ManosHacker 22:31, 21 Ιουλίου 2010 (UTC)
Στις σημειώσεις έγραφα για το μέγεθος του ταλαντωτή σε σχέση με την τάξη μεγέθους των αποστάσεων στο κρυσταλλικό πλέγμα. Αν υφίσταται μηχανική ταλάντωση υπάρχει και πλάτος ταλάντωσης, μήκος κύματος κλπ. Θα με ενδιέφερε να δείξω τι είναι αυτό στο φωνόνιο που ταλαντώνεται μοναδιαία και ταυτόχρονα μηχανικά, αν είναι ένα άτομο στο πλέγμα ή κάποια άτομα μαζί σε επίπεδο κρυστάλλου. Στην ουσία επειδή υπάρχει διαφοροποίηση ανά κρυσταλλικό πλέγμα δε γίνεται εύκολα και θέλησα να δώσω την τάξη μεγέθους του ελάχιστου μηχανικού ταλαντωτή παρόλα αυτά για να έχουν την αίσθηση όσοι διαβάζουν πού και πόσο βαθιά να ψάχνουν στις κλίμακες που φαντάζονται στο μυαλό τους. Υπάρχει κάτι να βοηθήσει στον οραματισμό του τι συμβαίνει εκεί μέσα και ταυτόχρονα να μην είναι ανάγκη να εκφράζεται με μαθηματικά; Κάνω λάθος και ο ελάχιστος ταλαντωτής για ένα φωνόνιο θα μπορούσε να αποτελείται από πολλαπλές επαναλήψεις κρυστάλλων; ManosHacker 10:51, 22 Ιουλίου 2010 (UTC)
Νομίζω πως έχει γίνει λάθος στο άρθρο. Δε μπορεί Ν να είναι ο συνολικός αριθμός των ατόμων στον κρύσταλλο. Ν πρέπει να είναι ο αριθμός των ατόμων (ή καλύτερα ταλαντωτών) που "χωράνε" σε ένα μήκος κύματος εντός του κρυστάλλου. Τα μαθηματικά αν δεν τα αντιστοιχίσεις διαισθητικά εύκολα σε φέρνουν σε λάθος. ManosHacker 15:05, 28 Ιουλίου 2010 (UTC)
Να πω καταρχήν τη γνώμη μου συνολικά: ότι είναι λίγο μπούρδα αυτό το φωνόνιο! :)))). Δηλαδή εντάξη ένα μαθηματικό μοντελάκι είναι. Δε ξέρω αν βοηθά ουσιαστικά σε κάτι για τη κατανόηση πρακτικά και τεχνολογικά της μετάδοσης του ήχου στα στερεά. Για τεχνολογική εφαρμογή πχ ένα μοντέλο ελαστικού συνεχούς μέσου (λέω τώρα) ή κάποιο άλλο μοντέλο με διακριτά άτομα αλλά πιο εμπειρικό και έυκολο στην επίλυση μπορεί να είναι πιο πρακτικό. Να σημειώσω ότι το απλούστερο μοντέλο, και από το οποίο είναι και το σχήμα, αφορά "πλέγμα" γραμμικό μονοδιάστατο. Δηλαδή τα ατομάκια είναι σε μια γραμμή στη σειρά, πεπερασμένα το πλήθος Ν και μάλιστα το τελευταίο είναι δίπλα στο πρώτο. Δηλαδή σχηματίζουν δακτυλίδι. Αλλά εγώ καταλαβαίνω ότι αυτό δεν μας ενδιαφέρει και τόσο. Μας ενδιαφέρουν τα μαθηματικά της υπόθεσης. Τώρα να σημειώσω ένα σχόλιο που δεν είναι δικό μου αλλά από αγγλικό άρθρο: η ιστορία με το φωνόνιο λέει κάπου είναι προσπάθεια να αντιμετωπίσουμε "πρόβλημα πολλών σωμάτων". Λόγω της μεγάλης πολυπλοκότητας και δυσκολίας επιλύουμε πρώτα ένα στοιχειώδες μοντελάκι και χτίζουμε πάνω σαυτό τα πιο ρεαλιστικά μοντελάκια.--vanakaris 19:33, 28 Ιουλίου 2010 (UTC)
Ε ξέρω γω.. νομίζω είναι όλα τα άτομα Ν του πλέγματος. Το λέει κάπου ξεκάθαρα. Δεν το είδα σε ορίτζιναλ πηγή, γιατί το αγγλικό δεν έχει ορίτζιναλ πηγές πχ σε pdf. Αλλά βάση της εμπειρίας μου από τη σχολή σε επίλυση διαφορικών το "επαλήθευσα" με βάση το γεγονός ότι μόνο για πολλά άτομα γίνεται το φωνόνιο τόσο μαθηματικά χρήσιμο, σχεδόν αναγκαίο (δες το σημείο με τον μετασχηματισμό Φουριέ στο αγγλικό, που πάμε από το πρόβλημα ως προς την κίνηση των ατόμων στο μετασχηματισμένο πρόβλημα ως προς τη κίνηση των φωνονίων). Τόσο μαθηματικά αναγκαίο λοιπόν που αποτελεί "γεγονός" ότι καλύτερα να υποθέσουμε φωνόνια παρά ταλάντωση ατόμων. Εγώ τουλάχιστον έτσι το καταλαβαίνω. Θα το ξανακοιτάξω αλλά νομίζω είναι ουσιώδες σημείο της όλης υπόθεσης ότι μιλάμε για μοντέλο ολόκληρου του κρυστάλλου.--vanakaris 19:33, 28 Ιουλίου 2010 (UTC)
Μήπως τελικά λέμε το ίδιο πράγμα? Δηλαδή το μήκος κύματος είναι
όπου n=0,1,2,...,N
και n=1 είναι το "ένα φωνόνιο" ή ισοδύναμα το πρώτο "κανονικό mode" ταλάντωσης
n=2 είναι τα "δύο φωνόνια" ή ισοδύναμα το δευτερο "κανονικό mode" ταλάντωσης
κ.ο.κ. Ν είναι το συνολικό πλήθος των ταλαντωτών του κρυστάλλου, το οποίο ταυτίζεται με τον αριθμό των ατόμων που χωράνε στο μέγιστο μήκος κύματος για αυτόν το κρύσταλλο. Το μέγιστο μήκος κύματος είναι, για n=1, λ= 2Νa. Το ελάχιστο μήκος κύματος είναι, για n=Ν, αυτό που προκύπτει από την απόσταση a μεταξύ των ατόμων. Δες σχήμα πάνω με τη χορδή δεξιά πάνω πάνω: το μήκος της χορδής είναι 1/2 του μέγιστου μήκους κύματος. Όμοια ο συνολικός αριθμός των ατόμων του κρυστάλλου επί την απόσταση a μεταξύ δύο ατόμων είναι το 1/2 του μέγιστου μήκους κύματος, σε συμφωνία με τον προηγούμενο τύπο.--vanakaris 11:32, 29 Ιουλίου 2010 (UTC)
- "Το μέγεθος του κβάντου δεν είναι σταθερό όπως στα φωτόνια, αλλά εξαρτάται από το πλήθος Ν των ατόμων ολόκληρου του πλέγματος που εξετάζεται". Αυτό με μπερδεύει καθώς έτσι το κβάντο ορίζεται μη επαρκώς και σχετικά. Με κάνει και φαντάζομαι πως ένα πιο μεγάλο κομμάτι του υλικού θα μου δίνει διαφορετικό κβάντο ενέργειας, ενώ στην πραγματικότητα μου δίνει με το ίδιο κβάντο μεγαλύτερα δυνατά μήκη κύματος προς διάδοση. Νομίζω πως το κβάντο (=φωνόνιο =μονάδα ενέργειας ταλάντωσης) έχει να κάνει με το μέγεθος, τη γεωμετρία και τη φύση του κρυστάλλου που συνεπάγεται τον ελάχιστο ταλαντωτή. Γι αυτό είχα γράψει "Το μέγεθος του ελάχιστου ταλαντωτή κάποιου κρυσταλλικού πλέγματος είναι συγκρίσιμο με τις αποστάσεις των ατόμων στον κρύσταλλο" στην ίδια σημείωση, με σκοπό να διαισθανθούν οι αναγνώστες το τι περίπου ταλαντώνεται ως φωνόνιο. ManosHacker 19:02, 29 Ιουλίου 2010 (UTC)
- Για άπειρο Ν θα έχουμε συνεχές, για πεπερασμένο Ν προκύπτει η κβάντωση. Με βάση το Ν, δηλαδή έχει νομίζω το Ν στον παρανομαστή. Πολύ λογικό αυτό που λες αλλά δεν ξέρω αν προκύπτει από τα μαθηματικά, θέλει λίγο ψάξιμο. Άν είσαι σίγουρος ότι το καταλαβαίνω λάθος και το πακέτο ενέργειας είναι κάποια σταθερά της φύσης του ατόμου και όχι κάτι που προκύπτει από τα μαθηματικά κρυστάλλου με Ν άτομα διόρθωσε το. Και μένα μου έκανε εντύπωση γιαυτό έβαλα τη νότα άλλωστε.--vanakaris 06:55, 30 Ιουλίου 2010 (UTC)
- Για άπειρο Ν θα έχουμε συνεχές, για πεπερασμένο Ν προκύπτει η κβάντωση. Με βάση το Ν, δηλαδή έχει νομίζω το Ν στον παρανομαστή. Πολύ λογικό αυτό που λες αλλά δεν ξέρω αν προκύπτει από τα μαθηματικά, θέλει λίγο ψάξιμο. Άν είσαι σίγουρος ότι το καταλαβαίνω λάθος και το πακέτο ενέργειας είναι κάποια σταθερά της φύσης του ατόμου και όχι κάτι που προκύπτει από τα μαθηματικά κρυστάλλου με Ν άτομα διόρθωσε το. Και μένα μου έκανε εντύπωση γιαυτό έβαλα τη νότα άλλωστε.--vanakaris 06:55, 30 Ιουλίου 2010 (UTC)
- Η ενέργεια ή ακριβέστερα ο κυματαριθμός ενός "πακέτου" είναι λέει

Λοιπόν. Για αρχή. Ο «τρόπος ταλάντωσης» είναι συνωνυμία για το «στάσιμο κύμα» και όχι για το φωνόνιο που απλά κβαντίζει τα στάσιμα κύματα που αναπτύσσονται σε ένα υλικό. Το βιβλίο, σε κάποια στιγμή που απλά βολεύει μαθηματικά, χάνοντας το φυσικό νόημα, περνά στις εξισώσεις του αρμονικού ταλαντωτή για να μπορέσει να καταλήξει εκεί που θέλει. Αποτέλεσμα: η μπαρούφα στην κύρια σελίδα της Βικιπαίδειας και η εντύπωσή της στο ευρύ κοινό. Κοινώς πίκρα γιατί όσα παράξενα μου έκαναν εντύπωση ως παιδί τα θυμάμαι ακόμα και κάνω μπουρμπουλήθρες να απωθώ τους λάθος συνειρμούς μου. Μετά: Το μήκος του ελάχιστου ταλαντωτή στο κρυσταλλικό πλέγμα είναι 2*α, όπου α η απόσταση μεταξύ των ατόμων του κρυσταλλικού πλέγματος που καθορίζει και την ενέργεια του φωνονίου. Απόσταση που μεταβάλλεται με τη διεύθυνση διάδοσης βεβαίως βεβαίως σύμφωνα με την ιδιοσυγκρασία του κρυστάλλου. Και φυσικά με τη θερμοκρασία που διαστέλλει και συστέλλει αλλάζοντας ενδοατομικές αποστάσεις στο πλέγμα. Έπειτα: Η ενέργεια του φωνονίου δεν αλλάζει αν αλλάξουμε τις διαστάσεις του σώματος του υλικού. Οι διαστάσεις του υλικού χρειάζονται για ένα λόγο: Αν η απόσταση των ατόμων στο πλέγμα είναι το μισό του μήκους κύματος που διαδίδεται το κβάντο - φωνόνιο, καθορίζει δηλαδή τη μέγιστη δυνατή συχνότητα που είναι δυνατό να διέλθει από το υλικό, το μέγεθος του κρυστάλλου δίνει το όριο για την ελάχιστη συχνότητα που μπορεί να συντηρήσει μέσα εκεί ένα στάσιμο κύμα. Ακόμα: Το φωνόνιο είναι η κόλλα των ηλεκτρονίων που τα δένει μαζί στην υπεραγωγιμότητα. Και τέλος: το φωνόνιο δεν είναι μαθηματικός φορμαλισμός. Τέτοιο πράγμα είναι ο αρμονικός ταλαντωτής που μπήκε σφήνα για να γλιτώσουμε πράξεις και που τελικά μας βάζει σφάλμα. Σφάλμα γιατί τα μαθηματικά της παραδοχής προϋποθέτουν την απειρία του κρυστάλλου ενώ εμείς έχουμε πεπερασμένο μήκος. ![]() ManosHackertalk 01:34, 15 Σεπτεμβρίου 2010 (UTC)
ManosHackertalk 01:34, 15 Σεπτεμβρίου 2010 (UTC)
Συμφ με σχήμα, το μέγεθος του "κβάντου" αντιστοιχεί στο σημείο που η κόκκινη καμπύλη (συχνότητα φωνονίου σε συνάρτηση με κυματαριθμό) περνάει σχεδόν από την αρχή των αξόνων. Δηλαδή το μέγεθος του κρυστάλλου δίνει το όριο για την ελάχιστη συχνότητα όπως σωστά λες. Δεν ξέρω ποιο από τα δύο συμβαίνει:
(i) μήπως έχεις την τάση να θεωρείς ως "φωνόνιο" το "φωνόνιο" κοντά στα πάνω άκρα, αριστερά και δεξιά της καμπύλης, δηλαδή μήκη κύματος κοντά στην απόσταση μεταξύ των ατόμων (αντίθετα εγώ θεωρώ ως "φωνόνιο" το ελάχιστο πακέτο ενέργειας, δηλ k κοντά στο μηδέν και μήκος κύματος της τάξης μεγέθους του μήκους κρυστάλλου) (τα τελευταία, με το μεγάλο μήκος κύματος τα λέει κάπου "ηχητικά" φωνόνια, ενώ αυτά με πολύ μικρό μήκος κύματος τα λέει "οπτικά" φωνόνια) ή
(ii) μήπως έχεις υπόψιν κάποιο αποτέλεσμα διαφορετικό από το .
Στην περίπτωση (i) είναι απλά θέμα ονοματολογίας, αν θα πείς το "φωνόνιο" στα πάνω άκρα "ένα φωνόνιο" με ενέργεια (ή κυματαριθμό) όπου n κοντά στο Ν ή θα το πείς n φωνόνια με ενέργεια το κάθε ένα n-οστό κανονικό mode που αντιστοιχεί σε ενέργεια ή n φωνόνια. Στην περίπτωση (ii) πλιζ δώσε το αποτέλεσμα--vanakaris 12:13, 15 Σεπτεμβρίου 2010 (UTC)
Όπα κάτσε γιατί τώρα το πιασα μια όντως μπαρούφα προσθήκη που έκανα. Εντάξη πιστεύω δικαιολογείται, ερασιτεχνική προσπάθεια είναι δεν είναι έγκριτο επιστημονικό περιοδικό ή θέση για διατριβή! Εννοώ ότι δεν είναι σωστή η λεζάντα που είχα βάλει στο σχήμα, προσπαθώντας να κάνω μια "κλασικιστική" διαισθητική απεικόνιση. Δεν είναι 1 φωνόνιο, 2 φωνόνια, 3 φωνόνια ... αυτό που "βλέπουμε", ούτε είναι διαδοχικά αποτελέσματα επιπλέον διέγερσης πακέτου hω. Διότι όλα αυτά τα modes συνυπάρχουν και γραμμικός συνδυασμός τους είναι η συνολική ταλάντωση. Αυτή η συνολική ταλάντωση δέχεται διεγέρσεις σε κβαντικά πακέτα hω, το κάθε hω είναι ένα φωνόνιο, αλλά δεν υπάρχει κάποια εικόνα με την οποία να μπορούμε να το "δούμε" με την κλασικιστική έννοια αυτό το φωνόνιο.--vanakaris 20:42, 15 Σεπτεμβρίου 2010 (UTC)
Δεν είναι εύκολο. Καθόμουν με καθηγητή που διδάσκει Κυματική και Στερεό και ψάχναμε τα βιβλία του και όλοι κάπου έχαναν το θέμα, πόσο μάλλον εμείς στη Βικιπαίδεια. Να θέσω τώρα το εξής σε σχέση με τη δεύτερη σημείωση: Το φωνόνιο κοντά στο απόλυτο μηδέν φτιάχνει «βαγονάκια» για τα ηλεκτρόνια που κάνουν το μέταλλο υπεραγωγό. Αν διπλασιάσουμε το μέγεθος του κρυστάλλου, διπλασιάσουμε δηλαδή το Ν, αλλοιώνουμε το φωνόνιο λες. Αν μόλις έχουμε φτάσει στη θερμοκρασία που το μέταλλο έγινε υπεραγωγός λοιπόν, έστω ένα διπλάσιο κομάτι του ίδιου μετάλλου δίπλα στο άλλο και άλλο ένα με μισό μήκος, στην ίδια θερμοκρασία όλα δηλαδή και δίπλα δίπλα. Υπάρχει περίπτωση κάποιο από τα δύο άλλα, είτε το διπλάσιο είτε το μισό σε μέγεθος, να μην είναι υπεραγωγός; ![]() ManosHackertalk 21:50, 15 Σεπτεμβρίου 2010 (UTC)
ManosHackertalk 21:50, 15 Σεπτεμβρίου 2010 (UTC)
Ένα σημείο δεν το έχω καθαρό. Το ελάχιστο κβάντο της ενέργειας μεταφέρεται ως κύμα που πατά πάνω στον ελάχιστο ταλαντωτή (άτομο, σε καθαρό μέταλλο έστω) με μήκος κύματος περίπου 2α (α η ενδοατομική απόσταση). Όλα καλά, βρήκα πόσο μεγάλο είναι το δικό μου φωνόνιο ή να το πω το μικρότερο δυνατό φωνόνιο! Διαιρώ το μήκος του κρυστάλλου με το Ν και νάτη η κλίμακα της χωρικής διάστασης του φωνονίου μου. Το θέμα είναι κατά πόσο ένα κύμα με μήκος κύματος Χ/500 ας πούμε, αν Χ το μήκος του κρυστάλλου, (έστω ένα μέτρο), συμπεριφέρεται σα κβαντομηχανικό σωματίδιο. Πρόκειται για φωνόνιο λοιπόν επίσης; Ξεφεύγει δηλαδή μήκος κύματος του φωνονίου από την κλίμακα κοντά στο 2α του ελάχιστου δυνατού μηχανικού ταλαντωτή μέσα στο πλέγμα; ![]() ManosHackertalk 22:20, 15 Σεπτεμβρίου 2010 (UTC)
ManosHackertalk 22:20, 15 Σεπτεμβρίου 2010 (UTC)
Άλλος συλλογισμός μου είναι ο εξής: Αν το "ελάχιστο" φωνόνιο οδεύοντας πέσει σε μια πλεγματική ατέλεια σκεδάζεται. Ένα σωματίδιο που μπορεί να ταξιδεύει μέσα στον κρύσταλλο χωρίς προβλήματα θα μπορούσε να είναι τουλάχιστο μερικές φορές μεγαλύτερο, να σερφάρει δηλαδή τα άτομα με μήκος κύματος ας πούμε 5 φορές το 2α. Θέλω να πω πως ένα φωνόνιο με μήκος κύματος ακριβώς 2α ή ελαφρά μεγαλύτερο κινδυνεύει εύκολα και σε μικρή απόσταση και να μην υφίσταται καν σε ένα κρύσταλλο που δεν είναι καθαρός. Θα μπορούσε να είναι πιο πρακτικό σαν φωνόνιο κάτι παραπάνω από το ελάχιστο θεωρητικό. Το θέμα είναι ως πού κλιμακώνεται αυτό, αν υπάρχει και απάντηση στην αμέσως προηγούμενη παράγραφο. Κάτι άλλο είναι το εξής: Το φωνόνιο μου θυμίζει τις θετικές οπές στους ημιαγωγούς. Δεν υπάρχει κάποιο σωματίδιο που να εντοπίζεται ως θετική οπή κι όμως μιλάμε για τις οπές και τις χρησιμοποιούμε λες και είναι αληθινές αφού η συμπεριφορά του κόσμου γύρω τους είναι σα να υπάρχουν πραγματικά. Μάλλον παρόμοιες ανάγκες μας αναγκάζουν να δεχόμαστε την ύπαρξη του φωνονίου ως "οντότητα" με φυσικό περιεχόμενο. ![]() ManosHackertalk 08:39, 16 Σεπτεμβρίου 2010 (UTC)
ManosHackertalk 08:39, 16 Σεπτεμβρίου 2010 (UTC)
βελτίωση
[επεξεργασία κώδικα]Νομίζω η ταλάντωση του ατόμου αφορά σε πολύ μικρά μήκη κύματος κ πολύ μεγάλες συχνότητες (μεγάλες ενέργειες, λεγόμενα "οπτικά φωνόνια"). Αλλά έχουμε και τα ηχητικά φωνόνια που αφορούν σε μεγάλα μήκη κύματος ("ηχητικά φωνόνια" που αφορούν στη διάδοση του ήχου).--vanakaris 17:18, 2 Οκτωβρίου 2010 (UTC)
- Μάλλον καλώς έβαλες την ταμπέλα. Το φωνόνιο διαισθάνομαι θα μπορούσε στα μέταλλα πχ να οριστεί πρακτικά και ως τη δεύτερη ζώνη Μπριλουίν γιατί στην πρώτη το φαινόμενο του aliasing θα μπορούσε να αλλοιώσει τοπικά, λόγω πλεγματικών ατελειών, τις μέγιστες συχνότητες διέλευσης. Οι ασφαλείς συχνότητες διέλευσης δηλαδή θα μπορούσαν να οριοθετούνται στη δεύτερη ζώνη Μπριλουίν ή και παραπάνω σε ένα αρκετά "βρώμικο" κρύσταλλο με ασυμμετρίες ή ασυνέχειες. Σε ακόμα πιο πολύπλοκα υλικά όπως το ξύλο τα φωνόνια παρατηρούνται αφού μεταφέρουν ήχο, βλέπουμε στάσιμα κύματα κλπ. Εκεί μπορεί να έχεις μικρότερο ελάχιστο ταλαντωτή τοπικά, καθώς όμως έχεις "νερά" με διαφορετικές πυκνότητες υλικού, η μέγιστη διαδιδόμενη συχνότητα είτε είναι πιο μικρή είτε καναλίζεται στα νερά του ξύλου όπου αυτό είναι πιο συμπαγές. Εν πάσει περιπτώσει το φωνόνιο στο ξύλο αντιστοιχεί σε πολύ μεγαλύτερα μήκη κύματος από τα μέταλλα, διέρχονται δηλαδή μικρότερες συχνότητες. Η παγίδευση "φωνονίων" μεγαλύτερων συχνοτήτων τοπικά θα εξηγούσε την κακή θερμική αγωγιμότητα του ξύλου και το ότι είναι εύφλεκτο, όμως αφού δε διαδίδεται σε όλο το μακροσκοπικό σύστημα δεν πρόκειται για φωνόνιο όπως το ορίζουμε. Το κακό στη Φυσική είναι πως κάνουμε πολλές παραδοχές για να κατανοήσουμε κάτι επαρκώς και τελικά φτάνουμε σε μαθηματικούς τύπους και μοντέλα που σπάνια ισχύουν.
 ManosHackertalk 18:39, 2 Οκτωβρίου 2010 (UTC)
ManosHackertalk 18:39, 2 Οκτωβρίου 2010 (UTC)




