Συνάρτηση Όιλερ

Στην θεωρία αριθμών, η συνάρτηση Όιλερ είναι η συνάρτηση $\phi :\mathbb {N} _{>0}\to \mathbb {N}$, όπου για κάθε θετικό ακέραιο $n$ το $\phi (n)$ μας δίνει το πλήθος των φυσικών αριθμών μικρότερων του $n$ οι οποίοι είναι σχετικά πρώτοι με τον $n$ (δηλαδή έχουν με τον $\,n$, μέγιστο κοινό διαιρέτη τη μονάδα).

Για παράδειγμα ας θεωρήσουμε τον αριθμό 9. Το $\phi (9)$ είναι ίσο με 6, αφού από τους φυσικούς αριθμούς από το 1 μέχρι το 9 ακριβώς έξι, οι 1, 2, 4, 5, 7 και 8, είναι πρώτοι ως προς το 9.

Η συνάρτηση του Όιλερ είναι πολύ χρήσιμη στην θεωρία αριθμών. Αρκεί και μόνο να παρατηρήσει κάποιος ότι το πλήθος των στοιχείων της πολλαπλασιαστικής ομάδας των ακεραίων modulo n είναι ακριβώς $\phi (n)$. Αυτό το γεγονός, μαζί με το θεώρημα του Λαγκράνζ, μας δίνουν την απόδειξη για το θεώρημα του Όιλερ, που αποτελεί γενίκευση του μικρού θεωρήματος του Φερμά.

Παραδείγματα

• Για $n=6$, έχουμε ότι $\phi (6)=2$, $1,5$ είναι πρώτοι με το $6$.
• Για $n=7$, έχουμε ότι $\phi (7)=6$, καθώς $1,2,3,4,5,6$ είναι πρώτοι με το $7$.
• Για $n=10$, έχουμε ότι $\phi (10)=4$, καθώς $1,3,7,9$ είναι πρώτοι με το $10$.
• Για $n=12$, έχουμε ότι $\phi (12)=4$, καθώς $1,5,7,11$ είναι πρώτοι με το $12$.

Ιστορία, ορολογία, συμβολισμός

Ο Λέοναρντ Όιλερ εισήγαγε τη συνάρτηση το 1763, αλλά χωρίς να τη συμβολίσει. Το 1784 επέλεξε το ελληνικό γράμμα $\pi$ για το συμβολισμό της: $\pi D$ "το πλήθος των αριθμών, μικρότερων του $D$, που δεν έχουν κοινό διαιρέτη με το D"· ο ορισμός είναι ίδιος με αυτόν που χρησιμοποιούμε, εκτός από την περίπτωση $D=1$. To 1801 ο Γκάους χρησιμοποίησε τον συμβολισμό $\phi D$ στη διατριβή του "Disquisitiones Arithmeticae". Ονομάστηκε "η συνάρτηση $\phi$ του Όιλερ" ή "η συνάρτηση $\phi$" και γράφουμε $\phi (D)$.

Το 1879 ο Τζ. Συλβέστερ δημιούργησε τον όρο totient, έτσι τη λέμε "η συνάρτηση totient του Όιλερ". Γενίκευση της συνάρτησης είναι η totient του Τζόρνταν. Η "συνάρτηση $\phi$ του Όιλερ" να μη συγχέεται με τη "συνάρτηση του Όιλερ", που είναι μία σειρά q στη συνδυαστική και τη μιγαδική ανάλυση.

Οι αριθμοί που είναι μικρότεροι του $n$ και πρώτοι με αυτόν ονομάζονται totatives του $n$, π.χ. οι 1, 5 είναι totatives του 6. Υπάρχουν $\phi (6)=2$ τέτοιοι. Οι υπόλοιποι, δηλ. 2, 3, 4, 6 είναι εκείνοι που έχουν τουλάχιστον έναν κοινό παράγοντα με τον $n$· υπάρχουν $n-\phi (n)=6-2=4$ τέτοιοι και το πλήθος τους αυτό λέγεται cototient.

Ιδιότητες

Η συνάρτηση $\phi$ δεν ορίζεται στο $n=0$ και επίσης θεωρούμε ότι $\phi (1)=1$.

1η ιδιότητα

Η συνάρτηση του Όιλερ είναι πολλαπλασιαστική, που σημαίνει ότι για κάθε δύο φυσικούς $m$, $n$ με $\mathrm {gcd} (m,n)=1$ ισχύει $\phi (mn)=\phi (m)\cdot \phi (n)$.

2η ιδιότητα

Είναι εύκολο να παρατηρήσει κάποιος ότι αν ο $n$ είναι πρώτος αριθμός τότε όλοι οι φυσικοί που είναι μικρότεροι από αυτόν είναι πρώτοι ως προς τον $n$, οπότε $\phi (n)=n-1$.

Για παράδειγμα: $\phi (101)=101-1=100$ επειδή το $101$ είναι πρώτος.

3η ιδιότητα

Αν $n=p^{k}$ για πρώτο αριθμό $p$ και $k\geq 1$ τότε

$\phi (p^{k})=p^{k-1}\cdot (p-1)=p^{k}\left(1-{\frac {1}{p}}\right).$

Για παράδειγμα $\phi (81)=\phi (3^{4})=3^{4-1}\cdot (3-1)=3^{3}\cdot 2=54$ ή $\phi (3^{4})=3^{4}\cdot (1-1/3)=81(3-1)/3=54$.

Ο τύπος του Όιλερ

Με χρήση των παραπάνω και του Κινεζικού Θεωρήματος Υπολοίπων η τιμή της $\phi (n)$ μπορεί να υπολογιστεί με χρήση του θεμελιώδους θεωρήματος της αριθμητικής:

Αν $n=p_{1}^{k_{1}}\cdot \ldots \cdot p_{r}^{k_{r}}$, όπου τα $p_{j}$ είναι διακεκριμένοι πρώτοι αριθμοί, τότε

$\phi (n)=(p_{1}-1)p_{1}^{k_{1}-1}\cdot \ldots \cdot (p_{r}-1)p_{r}^{k_{r}-1}$.

Για παράδειγμα $\phi (72)=\phi (3^{2}\cdot 2^{3})=(3-1)\cdot 3^{2-1}\cdot (2-1)\cdot 2^{3-1}=2\cdot 3^{1}\cdot 1\cdot 2^{2}=24$.

Ο τελευταίος τύπος μπορεί να γραφτεί και ως εξής:

$\phi (n)=p_{1}^{k_{1}}\cdot \left(1-{\frac {1}{p_{1}}}\right)\cdot \ldots \cdot p_{r}^{k_{r}}\cdot \left(1-{\frac {1}{p_{r}}}\right)=n\cdot \left(1-{\frac {1}{p_{1}}}\right)\cdot \ldots \cdot \left(1-{\frac {1}{p_{r}}}\right)$.

Για παράδειγμα $\phi (36)=\phi (3^{2}2^{2})=36\left(1-{\frac {1}{3}}\right)\left(1-{\frac {1}{2}}\right)=36\cdot {\frac {2}{3}}\cdot {\frac {1}{2}}=12$.

4η ιδιότητα

Πιο πάνω υπολογίσαμε το $\phi (9)$. Οι διαιρέτες του 9 είναι οι 1, 3, 9 με $\phi (1)=1$, $\phi (3)=2$, $\phi (9)=6$. Ο Γκάους παρατήρησε ότι $\phi (1)+\phi (3)+\phi (9)=1+2+6=9$ και γενικότερα

$\sum _{d\mid n}\phi (d)=n$,

όπου $d$ είναι όλοι οι (θετικοί) διαιρέτες του $n$.

Για παράδειγμα τα κλάσματα $1/9,2/9,3/9,4/9,5/9,6/9,7/9,8/9,9/9$ αν απλοποιηθούν δίνουν $1/9,2/9,1/3,4/9,5/9,2/3,7/9,8/9,1/1$.

Οι παρονομαστές είναι όλοι οι διαιρέτες του 9: 9,3, 1. Πόσα έχουν παρονομαστή το 9; όσα ο αριθμητής τους δεν είχε κοινό διαιρέτη με το 9, δηλ. $\phi (9)$. Πόσα έχουν παρονομαστή το 3; $\phi (3)$. Πόσα το 1; $\phi (1)$. Και αυτά είναι όλα τα κλάσματα. Συνολικά είναι 9, δηλ. $\phi (9)+\phi (3)+\phi (1)=9$.

Παρατήρηση

Μπορούμε να πάρουμε έναν άλλο τύπο για την $\phi (n)$, χρησιμοποιώντας την αντιστροφή του Μέμπιους στο άθροισμα 

$n=\sum _{d\mid n}\phi (d)$.

Ο τύπος αυτός είναι ο εξής:

$\phi (n)=\sum _{d\mid n}d\cdot \mu (n/d)$,

όπου με $\mu$ συμβολίζουμε την συνάρτηση του Μέμπιους στους φυσικούς αριθμούς.

Άλλοι τύποι για τη συνάρτηση φ

• $a\mid b\implies \phi (a)\mid \phi (b)$.
• $\phi (mn)\phi (d)=\phi (m)\phi (n)d$, όπου d = μκδ(m, n)

Ειδικές περιπτώσεις:

• Για $m=2$, τότε έχουμε ότι

$\phi (2n)={\begin{cases}2\phi (n)&{\text{αν }}n{\text{ άρτιος}},\\(n)&{\text{αν }}n{\text{ περιττός}}.\end{cases}}$

• Για $m=n$ ο τύπος γίνεται

$\phi (n^{2})=n\cdot \phi (n)$

και γενικότερα

$\phi (n^{k})=n^{k-1}\cdot \phi (n)$.

• $\phi (\mathrm {gcd} (m,n))\cdot \phi (\mathrm {lcm} (m,n))=\phi (m)\cdot \phi (n)$,

που μοιάζει με τον τύπο $\mathrm {gcd} (m,n)\cdot \mathrm {lcm} (m,n)=m\cdot n$ (δείτε Ελάχιστο Κοινό Πολλαπλάσιο).

• Το $\phi (n)$ είναι άρτιος για $n\geq 3$. Ακόμη, αν ο $n$ έχει $r$ διακριτούς περιττούς παράγοντες τότε $2^{r}\mid \phi (n)$.

Μερικές τιμές της συνάρτησης

Οι πρώτες 143 τιμές (ακολουθία A000010 στην OEIS) εμφανίζονται στο γράφημα και στον πιο κάτω πίνακα:

Γράφημα των πρώτων 100 τιμών

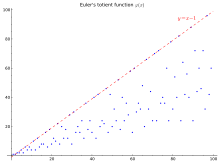
φ(n) for 1 ≤ n ≤ 143

+	0	1	2	3	4	5	6	7	8	9	10	11
0	N/A	1	1	2	2	4	2	6	4	6	4	10
12	4	12	6	8	8	16	6	18	8	12	10	22
24	8	20	12	18	12	28	8	30	16	20	16	24
36	12	36	18	24	16	40	12	42	20	24	22	46
48	16	42	20	32	24	52	18	40	24	36	28	58
60	16	60	30	36	32	48	20	66	32	44	24	70
72	24	72	36	40	36	60	24	78	32	54	40	82
84	24	64	42	56	40	88	24	72	44	60	46	72
96	32	96	42	60	40	100	32	102	48	48	52	106
108	36	108	40	72	48	112	36	88	56	72	58	96
120	32	110	60	80	60	100	36	126	64	84	48	130
132	40	108	66	72	64	136	44	138	48	92	70	120

Στο διάγραμμα η ευθεία y = n-1 είναι ένα άνω όριο και είναι ακριβώς αυτό στις περιπτώσεις όπου n = πρώτος. Δεν υπάρχει ευθεία που να είναι κάτω όριο.

Ασυμπτωτική τιμή

Για κάθε σύνθετο αριθμό $n>2$ έχουμε ότι

$\phi (n)>{\frac {n}{e^{\gamma }\cdot \log \log n+{\frac {3}{\log \log n}}}}$,

και

$\liminf _{n\to \infty }{\frac {\phi (n)}{n/\log \log n}}=e^{-\gamma }$,

όπου $\gamma$ είναι η σταθερά Όιλερ.

Επίσης, και για κάθε $n\geq 5$ ισχύει η απλουστευμένη ανισότητα

$\phi (n)>{\frac {n}{6\cdot \log \log n}}$.

Εφαρμογές

Εφαρμογή στο θεώρημα του Όιλερ

Το θεώρημα του Όιλερ λέει ότι αν $a$ και $n$ είναι σχετικά πρώτοι μεταξύ τους, τότε

$a^{\phi (n)}\equiv 1\mod n$.

Το μικρό θεώρημα του Φερμά είναι η ειδική περίπτωση που το $n$ είναι πρώτος και τότε

$a^{n-1}\equiv 1\mod n$,

καθώς $\phi (n)=n-1$.

Εφαρμογή στην κρυπτογραφία RSA

Στην κρυπτογραφία RSA ξεκινάμε με δύο μεγάλους πρώτους $p$, $q$. Για χάριν ευκολίας ας υποθέσουμε ότι είναι $p=5$, $q=11$. Παίρνουμε το γινόμενό τους $n=pq=55$ και το $\phi (n)=\phi (55)=40$. Διαλέγουμε έναν αριθμό $e<\phi (n)$ έτσι ώστε $e$ και $\phi (n)$ είναι σχετικά πρώτοι μεταξύ τους, ας είναι το $e=7$. Υπολογίζουμε τον αντίστροφό του $\mathrm {mod} \ \phi (n))$ με τη βοήθεια του αλγορίθμου του Ευκλείδη, που είναι το $d=23$. Πράγματι $7\cdot 23=161=1{\pmod {40}}$. To δημόσιο κλειδί είναι το ζεύγος $(e,n)=(7,55)$ και το ιδιωτικό κλειδί είναι το $(d,n)=(23,55)$. Αν ξέρει κάποιος άλλος το $(e,n)$ δεν μπορεί (εύκολα) να βρει το $d$ αν δεν ξέρει το $\phi (n)$, καθώς οι γνωστοί αλγόριθμοι στηρίζονται στην παραγοντοποίηση του $n$. Μέχρι στιγμής, δεν είναι γνωστός κάποιος αλγόριθμος που γρήγορα παραγοντποιεί αριθμούς (δηλαδή αλγόριθμος που τρέχει σε πολυωνυμικό χρόνο) και αυτό εγγυάται ότι δεν θα βρει κάποιος άλλος το ιδιωτικό κλειδί.

Τέλος για να κρυπτογραφήσουμε ένα μήνυμα (δηλαδή έναν αριθμό) $m$, τον υψώνουμε στην δύναμη $e$, δηλαδή στέλνουμε $m^{e}(\mathrm {mod} \ m)$. Ο παραλήπτης υψώνει αυτό που έλαβε στη δύναμη $d$ και λαμβάνει το $(m^{e})^{d}\equiv m^{ed}\equiv m^{1}\equiv m{\pmod {1}}$, δηλαδή το αρχικό μήνυμα.

Εφαρμογή στην κυκλοτομία

Στο τελευταίο κεφάλαιο του έργου του Disquisitiones ο Καρλ Φρίντριχ Γκάους αποδεικνύει ότι ένα κανονικό $n$-γωνο μπορεί να κατασκευαστεί με κανόνα και διαβήτη αν το $\phi (n)$ είναι δύναμη του $2$.

Αναλύουμε τον $n$ σε γινόμενο πρώτων παραγόντων. Τότε:

1. Αν $n=2^{k}$ τότε $\phi (n)=2^{k-1}$ είναι δύναμη του $2$ και το πολύγωνο κατασκευάζεται: $2,4,8,16,32,\ldots$

1. Αν $n=p^{k}$ όπου $p$ είναι πρώτος μεγαλύτερος του 2, τότε $\phi (n)=p^{k-1}\cdot (p-1)$, που για να είναι δύναμη του $2$ πρέπει $k=1$ και $p-1$ να είναι δύναμη του $2$. Οι αριθμοί αυτοί $p$ λέγονταιπρώτοι αριθμοί του Φερμά και είναι γνωστοί οι εξής: 3, 5, 17, 257, 65537. Δεν ξέρουμε αν υπάρχουν άλλοι.

1. Συνδυασμός των παραπάνω: $2\cdot 3,2\cdot 5,2^{2}\cdot 3,3\cdot 5,2^{2}\cdot 5,2^{3}\cdot 3,2\cdot 3\cdot 5,2\cdot 17,2^{3}\cdot 5,\ldots$

Τελικά τα κατασκευάσιμα κανονικά πολύγωνα είναι 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40, ... (ακολουθία A003401 στην OEIS).

Περαιτέρω ανάγνωση

Ελληνικά άρθρα

• Π. Μαρουσάκης (1978). «Η Αριθμοθεωρητική Συνάρτηση φ(Α) του Euler». Ευκλείδης Β΄ (4): 193-194. http://www.hms.gr/apothema/?s=sa&i=4282. 

Ξενόγλωσσα άρθρα

• Moser, Leo (Ιανουαρίου 1949). «Some Equations Involving Euler's Totient Function». The American Mathematical Monthly 56 (1): 22. doi:10.2307/2305815. https://archive.org/details/sim_american-mathematical-monthly_1949-01_56_1/page/22. 
• Shiu, Peter (2013). «97.02 Solutions to φ (m) = k! and σ (n) = k!». The Mathematical Gazette 97 (538): 110-115. https://www.jstor.org/stable/24496766. 
• Freed-Brown, Julian; Holden, Matthew; Orrison, Michael E.; Vrable, Michael (Φεβρουαρίου 2012). «Cyclotomic Polynomials, Symmetric Polynomials, and a Generalization of Euler's Totient Function». Mathematics Magazine 85 (1): 44–50. doi:10.4169/math.mag.85.1.44. https://archive.org/details/sim_mathematics-magazine_2012-02_85_1/page/44. 
• Tou, Erik R. «Math Origins: The Totient Function». MAA. Ανακτήθηκε στις 8 Σεπτεμβρίου 2023. 

Βιβλιογραφία

• Abramowitz, M.· Stegun, I. A. (1964). «24.3.2». Handbook of Mathematical Functions. New York: Dover Publications. ISBN 0-486-61272-4. 
• Bach, Eric· Shallit, Jeffrey (1996). Algorithmic Number Theory (Vol I: Efficient Algorithms). Cambridge, MA: MIT Press Series in the Foundations of Computing. ISBN 0-262-02405-5. 
• Ford, Kevin (1999). «The number of solutions of φ(x) = m». Annals of Mathematics 150 (1): 283–311. doi:doi:10.2307/121103. ISSN 0003-486X. . 
• Gauss, Carl Friedrich (1986). Disquisitiones Arithmeticae. Μτφρ. Clarke, Arthur A. (2η έκδοση). New York: Springer. ISBN 0-387-96254-9. 
• Graham, Ronald· Knuth, Donald· Patashnik, Oren (1994). Concrete Mathematics: a foundation for computer science (2η έκδοση). Reading, MA: Addison-Wesley. ISBN 0-201-55802-5. 
• Guy, Richard K. (2004). Unsolved Problems in Number Theory, Problem Books in Mathematics (3η έκδοση). New York, NY: Springer-Verlag. ISBN 0-387-20860-7. 
• Hardy, G. H.· Wright, E. M. (1979). An Introduction to the Theory of Numbers (5η έκδοση). Oxford: Oxford University Press. ISBN 978-0-19-853171-5. 
• Long, Calvin T. (1972). Elementary Introduction to Number Theory (2η έκδοση). Lexington: D. C. Heath and Company. LCCN 77-171950. 
• Pettofrezzo, Anthony J.· Byrkit, Donald R. (1970). Elements of Number Theory. Englewood Cliffs: Prentice Hall. LCCN 77-81766. 
• Ribenboim, Paulo (1996). The New Book of Prime Number Records (3η έκδοση). New York: Springer. ISBN 0-387-94457-5. 
• Sandifer, Charles (2007). The early mathematics of Leonhard Euler. MAA. ISBN 0-88385-559-3. 
• Sándor, József· Mitrinović, Dragoslav S.· Crstici, Borislav, επιμ. (2006). Handbook of number theory I. Dordrecht: Springer-Verlag. σελίδες 9–36. ISBN 1-4020-4215-9. 
• Sándor, Jozsef· Crstici, Borislav (2004). Handbook of number theory II. Dordrecht: Kluwer Academic. σελίδες 179–327. ISBN 1-4020-2546-7. 
• Schramm, Wolfgang (2008). «The Fourier transform of functions of the greatest common divisor». Electronic Journal of Combinatorial Number Theory 8 (1). 
• Βλάμος Π., Ράππος Ε. «Η συνάρτηση φ του Euler Αρχειοθετήθηκε 2019-01-16 στο Wayback Machine.», σελ.96-103, από Ελληνική Ψηφιακή Μαθηματική Βιβλιοθήκη Αρχειοθετήθηκε 2019-07-26 στο Wayback Machine.. Αρχειοθετήθηκε 16/01/2019. Ανακτήθηκε 16/01/2019.