Χαοτική ανάμειξη

Στη θεωρία του χάους και τη δυναμική των ρευστών, η χαοτική ανάμιξη είναι μια διαδικασία κατά την οποία οι ιχνηθέτες ροής μετατρέπονται σε πολύπλοκα φράκταλ υπό τη δράση μιας ροής ρευστού, η οποία χαρακτηρίζεται από Εκθετική αύξηση των νημάτων του ρευστού.^[1]^[2] Ακόμη και πολύ απλές ροές, όπως η δίνη που αναβοσβήνει, ή πεπερασμένα πεδία ανέμου μπορούν να δημιουργήσουν εξαιρετικά πολύπλοκα μοτίβα από αρχικά απλά πεδία ιχνηθετών^[3].

Το φαινόμενο δεν έχει κατανοηθεί επαρκώς μέχρι σήμερα και αποτελεί αντικείμενο πολλών ερευνών.

Πλαίσιο της χαοτικής μεταφοράς

Ροές ρευστών

Δύο βασικοί μηχανισμοί είναι υπεύθυνοι για την ανάμιξη των ρευστών: η διάχυση και η μεταφορά. Στα υγρά, η μοριακή διάχυση από μόνη της είναι ελάχιστα αποτελεσματική για την ανάμιξη. Για την καλύτερη ανάμιξη απαιτείται η μεταφορά της ύλης από τη ροή.

Η ροή των ρευστών συμμορφώνεται με τις θεμελιώδεις εξισώσεις της δυναμικής των ρευστών (όπως η διατήρηση της μάζας και η διατήρηση της ορμής) που ονομάζονται εξισώσεις Ναβιέρ-Στόκες. Οι εξισώσεις αυτές γράφονται για το Eulerian πεδίο ταχύτητας και όχι για τη θέση Λαγκράνζ των σωματιδίων του ρευστού. Οι λαγκρανζιανές τροχιές λαμβάνονται στη συνέχεια με ολοκλήρωση της ροής. Η μελέτη της επίδρασης της συμβολής στην ανάμιξη ρευστών ισοδυναμεί με την περιγραφή του τρόπου με τον οποίο διαφορετικά σωματίδια ρευστού Λαγκράνζ εξερευνούν το πεδίο του ρευστού και διαχωρίζονται το ένα από το άλλο.

Συνθήκες για χαοτική μεταφορά

Μια ροή ρευστού μπορεί να θεωρηθεί ως ένα δυναμικό σύστημα, δηλαδή ένα σύνολο συνήθων διαφορικών εξισώσεων που καθορίζουν την εξέλιξη μιας τροχιάς Λαγκράνζ. Οι εξισώσεις αυτές ονομάζονται εξισώσεις μεταφοράς:

{\frac {d{\vec {x}}}{dt}}={\vec {v}}({\vec {x}},t)

όπου ${\vec {v}}=(u,v,w)$ είναι οι συνιστώσες του πεδίου ταχύτητας, οι οποίες θεωρούνται γνωστές από τη λύση των εξισώσεων που διέπουν τη ροή των ρευστών, όπως οι εξισώσεις Ναβιέρ-Στόκες, και ${\vec {x}}=(x,y,z)$ είναι η φυσική θέση. Εάν το δυναμικό σύστημα που διέπει τις τροχιές είναι χαοτικό, η ολοκλήρωση μιας τροχιάς είναι εξαιρετικά ευαίσθητη στις αρχικές συνθήκες και τα γειτονικά σημεία διαχωρίζονται εκθετικά με το χρόνο. Το φαινόμενο αυτό ονομάζεται χαοτική μεταφορά.

Τα δυναμικά συστήματα και η θεωρία του χάους ισχυρίζονται ότι τουλάχιστον 3 βαθμοί ελευθερίας είναι απαραίτητοι για να είναι ένα δυναμικό σύστημα χαοτικό. Οι τρισδιάστατες ροές έχουν τρεις βαθμούς ελευθερίας που αντιστοιχούν στις τρεις συντεταγμένες και συνήθως οδηγούν σε χαοτική μεταφορά, εκτός αν η ροή έχει συμμετρίες που μειώνουν τον αριθμό των βαθμών ελευθερίας. Σε ροές με λιγότερους από 3 βαθμούς ελευθερίας, οι τροχιές Λαγκράνζ περιορίζονται σε κλειστούς σωλήνες και η ανάμιξη που προκαλείται από διάτμηση μπορεί να συνεχιστεί μόνο εντός αυτών των σωλήνων.

Αυτό ισχύει για δισδιάστατες στάσιμες ροές στις οποίες υπάρχουν μόνο δύο βαθμοί ελευθερίας $x$ και $y$ . Για στάσιμες (χρονικά ανεξάρτητες) ροές, οι τροχιές των σωματιδίων του ρευστού κατά Λαγκράνζ συμπίπτουν με τις γραμμές ροής της ροής, που είναι απομονωμένες γραμμές της συνάρτησης ροής. Σε 2-D, οι γραμμές ροής είναι ομόκεντρες κλειστές καμπύλες που διασταυρώνονται μόνο σε σημεία στασιμότητας. Έτσι, μια κηλίδα βαμμένου ρευστού προς ανάμιξη μπορεί να εξερευνήσει μόνο την περιοχή που οριοθετείται από την πιο εξωτερική και την πιο εσωτερική γραμμή ροής, στην οποία βρίσκεται την αρχική στιγμή. Όσον αφορά τις πρακτικές εφαρμογές, αυτή η διαμόρφωση δεν είναι πολύ ικανοποιητική.

Για 2-D μη σταθερές (χρονικά εξαρτώμενες) ροές, οι στιγμιαίες κλειστές γραμμές ροής και οι τροχιές του Λαγκράνζ δεν συμπίπτουν πλέον. Ως εκ τούτου, οι τροχιές κατά Λαγκράνζ εξερευνούν μεγαλύτερο όγκο του όγκου, με αποτέλεσμα την καλύτερη ανάμιξη. Παρατηρείται χαοτική μεταφορά για τις περισσότερες δισδιάστατες μη σταθερές ροές. Ένα διάσημο παράδειγμα είναι η ροή στροβίλου που αναβοσβήνει (blinking vortex flow) που εισήγαγε ο Αρέφ,^[4] όπου δύο σταθεροί ραβδοειδείς αναδευτήρες περιστρέφονται εναλλάξ μέσα στο ρευστό. Η περιοδική εναλλαγή του ενεργού (περιστρεφόμενου) αναδευτήρα εισάγει μια χρονική εξάρτηση στη ροή, η οποία οδηγεί σε χαοτική συμβολή. Οι λαγκρανζιανές τροχιές μπορούν επομένως να ξεφύγουν από κλειστές γραμμές ροής και να επισκεφθούν ένα μεγάλο τμήμα του πεδίου του ρευστού.

Ψαλιδισμός

Μια ροή προωθεί την ανάμιξη διαχωρίζοντας γειτονικά σωματίδια ρευστού. Αυτός ο διαχωρισμός συμβαίνει λόγω των κλίσεων ταχύτητας, ένα φαινόμενο που ονομάζεται διάτμηση. Έστω ${\vec {x}}_{1}$ και ${\vec {x}}_{2}$ δύο γειτονικά σωματίδια ρευστού, που χωρίζονται κατά $\delta {\vec {x}}={\vec {x}}_{2}-{\vec {x}}_{1}$ τη χρονική στιγμή t. Όταν τα σωματίδια προωθούνται από μια ροή v → ${\vec {v}}$ , τη χρονική στιγμή $t+\delta t$ ο προσεγγιστικός διαχωρισμός μεταξύ των σωματιδίων μπορεί να βρεθεί μέσω της σειράς Τέιλορ:

{\frac {\mathrm {d} }{\mathrm {d} t}}({\vec {x}}+\delta {\vec {x}})\approx {\vec {v}}+\nabla {\vec {v}}\cdot \delta {\vec {x}}

ως εκ τούτου

\delta x(t+\delta t)\approx \delta x(t)+\delta t(\delta x\cdot \nabla ){\vec {v}}

και

{\frac {\mathrm {d} }{\mathrm {d} t}}\delta {\vec {x}}\approx \nabla {\vec {v}}\cdot \delta {\vec {x}}

Ο ρυθμός αύξησης του διαχωρισμού δίνεται επομένως από την κλίση του πεδίου ταχύτητας προς την κατεύθυνση του διαχωρισμού. Η ροή επίπεδης διάτμησης είναι ένα απλό παράδειγμα σταθερής ροής μεγάλης κλίμακας που παραμορφώνει τα στοιχεία του ρευστού λόγω ομοιόμορφης διάτμησης.

Χαρακτηρισμός της χαοτικής συμβολής

Εκθέτες Λιαπούνοφ

Εάν η ροή είναι χαοτική, τότε μικρά αρχικά σφάλματα, $\delta {\vec {x}}$ , σε μια τροχιά θα αποκλίνουν εκθετικά. Αυτό που μας ενδιαφέρει είναι να υπολογίσουμε τη σταθερότητα - δηλαδή πόσο γρήγορα αποκλίνουν οι κοντινές τροχιές. Ο πίνακας Ιακόμπι του πεδίου ταχύτητας, $\nabla {\vec {v}}$ , παρέχει πληροφορίες σχετικά με τον τοπικό ρυθμό απόκλισης των κοντινών τροχιών ή τον τοπικό ρυθμό διάτασης του χώρου Λαγκρανζιανής.

Ορίζουμε τον πίνακα H έτσι ώστε:

{\frac {\mathrm {d} }{\mathrm {d} t}}{\boldsymbol {H}}\equiv \nabla {\vec {v}}\cdot {\boldsymbol {H}},\qquad {\boldsymbol {H}}(t=0)={\boldsymbol {I}}

όπου I είναι ο πίνακας ταυτότητας. Προκύπτει ότι:

\delta {\vec {x}}(t)\approx {\boldsymbol {H}}\cdot \delta {\vec {x}}_{0}

Οι εκθέτες Λιαπούνοφ πεπερασμένου χρόνου ορίζονται ως ο χρονικός μέσος όρος των λογαρίθμων των μηκών των κύριων συνιστωσών του διανύσματος H κατά τη διάρκεια ενός χρόνου t:

{\boldsymbol {H^{T}}}\cdot {\boldsymbol {H}}\cdot \delta {\vec {x}}_{0i}=h_{i}\cdot \delta {\vec {x}}_{0i}

\lambda _{i}({\vec {x}},t)\equiv {\frac {1}{2t}}\ln {h_{i}({\vec {x}},t)}

όπου $\lambda _{i}({\vec {x}},t)\geq \lambda _{i+1}({\vec {x}},t)$ είναι ο i εκθέτης Λιαπούνοφ του συστήματος, ενώ $\delta {\vec {x}}_{0i}$ είναι η i-η κύρια συνιστώσα του πίνακα H.

Εάν ξεκινήσουμε με ένα σύνολο ορθοκανονικών αρχικών διανυσμάτων σφάλματος, $\{\delta {\vec {x}}_{0i}\}$ τότε ο πίνακας H θα τα αντιστοιχίσει σε ένα σύνολο τελικών ορθογώνιων διανυσμάτων σφάλματος μήκους $\{{\sqrt {h_{i}({\vec {x}},t)}}\}$ . Η δράση του συστήματος χαρτογραφεί μια απειροελάχιστη σφαίρα των αρχικών σημείων σε ένα ελλειψοειδές του οποίου ο μεγάλος άξονας δίνεται από το ${\sqrt {h_{1}({\vec {x}},t)}}$ ενώ ο δευτερεύων άξονας δίνεται από την ${\sqrt {h_{N}({\vec {x}},t)}}$ , όπου Ν είναι ο αριθμός των διαστάσεων.^[5]^[6]

Αυτός ο ορισμός των εκθετών Λιαπούνοφ είναι πιο κομψός και πιο κατάλληλος σε πραγματικά δυναμικά συστήματα συνεχούς χρόνου από τον πιο συνηθισμένο ορισμό που βασίζεται σε χάρτες διακριτών συναρτήσεων. Η Θεωρία του Χάους ορίζεται ως η ύπαρξη τουλάχιστον ενός θετικού εκθέτη Λιαπούνοφ.

Σε ένα χαοτικό σύστημα, ονομάζουμε εκθέτη Λιαπούνοφ την ασυμπτωτική τιμή της μεγαλύτερης ιδιοτιμής του H:

\lambda =\lim _{t\to \infty }\lambda _{1}({\vec {x}},t)

Εάν υπάρχει σημαντική διαφορά μεταξύ των εκθετών Λιαπούνοφ, τότε καθώς ένα διάνυσμα σφάλματος εξελίσσεται προς τα εμπρός στο χρόνο, οποιαδήποτε μετατόπιση προς την κατεύθυνση της μεγαλύτερης αύξησης θα τείνει να μεγεθύνεται. Συνεπώς, η αύξηση του ποσοστού του σφάλματος θα είναι μεγαλύτερη από την αύξηση του ποσοστού του σφάλματος:

|\delta {\vec {x}}|\approx |\delta {\vec {x}}_{0}|e^{\lambda _{1}t}.

Ο εκθέτης Λιαπούνοφ μιας ροής είναι μια μοναδική ποσότητα που χαρακτηρίζει τον ασυμπτωτικό διαχωρισμό των σωματιδίων ρευστού σε μια δεδομένη ροή. Συχνά χρησιμοποιείται ως μέτρο της αποτελεσματικότητας της ανάμιξης, καθώς μετράει πόσο γρήγορα διαχωρίζονται οι τροχιές μεταξύ τους λόγω της χαοτικής μεταφοράς. Ο εκθέτης Λιαπούνοφ μπορεί να υπολογιστεί με διάφορες μεθόδους:

ακολουθώντας μια μοναδική τροχιά για πολύ μεγάλο χρονικό διάστημα και υπολογίζοντας $\lambda =\lim _{t\to \infty }\lambda _{1}({\vec {x}},t)$ .
ή ακολουθώντας ένα σύνολο τροχιών για μια δεδομένη χρονική περίοδο και υπολογίζοντας το μέσο όρο του συνόλου: $<\lambda >_{trajectories}$

Η ισοδυναμία των δύο μεθόδων οφείλεται στην εργοδικότητα του χαοτικού συστήματος.

Αύξηση των νηματίων σε σχέση με την εξέλιξη της κλίσης του ιχνηθέτη

Η ακόλουθη, ακριβής εξίσωση μπορεί να προκύψει από μια εξίσωση μεταφοράς-διάχυσης (βλέπε παρακάτω), με όρο διάχυσης (D=0) μηδέν:

{\frac {\mathrm {d} \nabla q}{\mathrm {d} t}}=-\nabla q\cdot \nabla {\vec {v}}

Παράλληλα με τον ορισμό του εκθέτη Λιαπούνοφ, ορίζουμε τον πίνακα ${\boldsymbol {H}}^{\prime }$ , ως εξής:

{\frac {\mathrm {d} {\boldsymbol {H^{\prime }}}}{\mathrm {d} t}}=-\nabla {\boldsymbol {H^{\prime }}}\cdot \nabla {\vec {v}}\qquad {\boldsymbol {H^{\prime }}}(t=0)={\boldsymbol {I}}

Είναι εύκολο να αποδειχθεί αυτό:

{\boldsymbol {H^{\prime }}}={\boldsymbol {H}}^{-1}

Αν ορίσουμε $\lbrace h_{i}^{\prime }\rbrace$ ως τα τετραγωνικά μήκη των κύριων συνιστωσών του ιχνηθέτη πίνακα κλίσης, ${\boldsymbol {H}}^{\prime }$ , τότε:

h_{i}^{\prime }=1/h_{i}

όπου τα $\lbrace h_{i}^{\prime }\rbrace$ είναι τοποθετημένα, όπως προηγουμένως, από το μεγαλύτερο προς το μικρότερο. Επομένως, η αύξηση του διανύσματος σφάλματος θα προκαλέσει αντίστοιχη μείωση του ιχνηθέτη κλίση και αντιστρόφως. Αυτό μπορεί να γίνει κατανοητό πολύ απλά και διαισθητικά με τη σχέση θεωρώντας δύο κοντινά σημεία: αφού η διαφορά στη συγκέντρωση του ιχνηθέτη θα είναι σταθερή, η μόνη πηγή μεταβολής των κλίσεων μεταξύ τους θα είναι η μεταξύ τους ο διαχωρισμός τους.^[5]^[7]

Σύγκλιση περιγράμματος

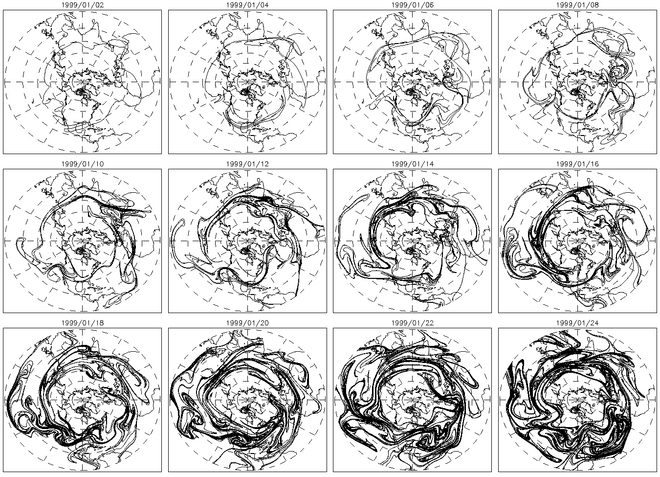
Εξέλιξη ενός περιγράμματος που διαχέεται

Η συμβολή περιγράμματος είναι μια άλλη χρήσιμη μέθοδος για τον χαρακτηρισμό της χαοτικής ανάμιξης. Στις χαοτικές ροές, τα μεταφερόμενα περιγράμματα αυξάνονται εκθετικά με την πάροδο του χρόνου. Το παραπάνω σχήμα δείχνει την εξέλιξη καρέ-καρέ ενός περιγράμματος που μεταφέρεται επί αρκετές ημέρες. Το σχήμα στα δεξιά δείχνει το μήκος αυτού του περιγράμματος ως συνάρτηση του χρόνου.

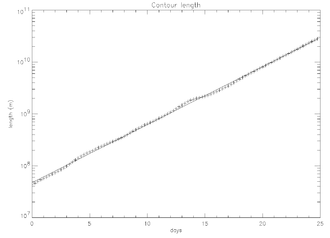
Η σύνδεση μεταξύ εκθετικής ανάπτυξης περιγράμματος και θετικών εκθετών Λιαπούνοφ είναι εύκολο να γίνει αντιληπτό. Ο ρυθμός αύξησης του περιγράμματος δίνεται ως εξής:

{\frac {\mathrm {d} L}{\mathrm {d} t}}=\int |\nabla {\vec {v}}\cdot \mathrm {d} {\vec {s}}|

όπου $\mathrm {d} {\vec {s}}$ είναι η διαδρομή και το ολοκλήρωμα εκτελείται στο μήκος του περιγράμματος. Οι ρυθμοί ανάπτυξης του περιγράμματος θα προσεγγίζουν το μέσο όρο των μεγάλων εκθετών Λιαπούνοφ:^[5]

L\approx L_{0}\exp({\bar {\lambda }}_{1}t)

Τομή Πουανκαρέ

Στη χαοτική μεταφορά, ένα σωματίδιο ρευστού κινείται μέσα σε μια μεγάλη περιοχή και συναντά άλλα σωματίδια που αρχικά βρίσκονταν σε απόσταση από αυτό. Ένα σωματίδιο μπορεί τότε να θεωρηθεί ότι αναμιγνύεται με σωματίδια που κινούνται στην ίδια περιοχή. Ωστόσο, η περιοχή που καλύπτεται από μια τροχιά δεν καλύπτει πάντα ολόκληρη την περιοχή του ρευστού. Οι τομές Πουανκαρέ χρησιμοποιούνται για τη διάκριση των περιοχών καλής και κακής ανάμιξης.

Ο χάρτης Πουανκαρέ ορίζεται ως ο μετασχηματισμός

{\begin{aligned}{\boldsymbol {M}}\colon {\vec {x_{i}}}(t_{i})&\to {\vec {x}}_{i+1}(t_{i+1}=t_{i}+T,{\vec {x_{i}}}).\end{aligned}}

${\boldsymbol {M}}$ μετατρέπει ένα σημειακό σωματίδιο στη θέση του σωματιδίου μετά από ένα χρονικό διάστημα T. Ειδικά, για μια χρονικά περιοδική ροή με περίοδο T, η εφαρμογή του χάρτη πολλές φορές σε ένα σωματίδιο δίνει τις διαδοχικές θέσεις του σωματιδίου από περίοδο σε περίοδο. Μια τομή Πουανκαρέ κατασκευάζεται ξεκινώντας από μερικές διαφορετικές αρχικές συνθήκες και σχεδιάζοντας τις αντίστοιχες επαναλήψεις. Αυτό καταλήγει στην απεικόνιση των τροχιών με στροβοσκοπική απεικόνιση κάθε T.

Ως παράδειγμα, το σχήμα που παρουσιάζεται εδώ (αριστερό μέρος) απεικονίζει την τομή Πουανκαρέ που προκύπτει όταν εφαρμόζουμε περιοδικά μια κίνηση τύπου οκτώ σε μια κυκλική ράβδο ανάμιξης. Ορισμένες τροχιές εκτείνονται σε μια μεγάλη περιοχή: αυτή είναι η χαοτική περιοχή ή περιοχή ανάμιξης, όπου συμβαίνει καλή ανάμιξη. Ωστόσο, υπάρχουν επίσης δύο "τρύπες": σε αυτές τις περιοχές, οι τροχιές είναι κλειστές. Αυτές ονομάζονται ελλειπτικές νησίδες, καθώς οι τροχιές στο εσωτερικό τους είναι καμπύλες που μοιάζουν με ελλειπτικές. Οι περιοχές αυτές δεν αναμειγνύονται με το υπόλοιπο ρευστό. Για εφαρμογές ανάμιξης, οι ελλειπτικές νησίδες πρέπει να αποφεύγονται για δύο λόγους :

Τα σωματίδια του ρευστού δεν είναι σε θέση να διασχίσουν τα όρια των νησίδων (εκτός από την αργή διάχυση), με αποτέλεσμα το διαχωρισμό.
Η ανάμιξη μέσα σε αυτές τις περιοχές δεν είναι αποτελεσματική, επειδή οι τροχιές είναι κλειστές και επομένως δεν είναι χαοτικές.

Για την αποφυγή μη χαοτικών νησιών, πρέπει να κατανοήσουμε τη φυσική προέλευση αυτών των περιοχών. Σε γενικές γραμμές, η αλλαγή της γεωμετρίας της ροής μπορεί να μεταβάλει την παρουσία ή την απουσία νησιών. Στη ροή σχήματος οκτώ, για παράδειγμα, για μια πολύ λεπτή ράβδο, η επίδραση της ράβδου δεν γίνεται αισθητή μακριά από τη θέση της και υπάρχουν σχεδόν κυκλικές τροχιές μέσα στους βρόχους της ροής σχήματος οκτώ. Με μια φαρδύτερη ράβδο (δεξιά πλευρά του σχήματος), τα σωματίδια μπορούν να διαφύγουν από αυτούς τους βρόχους και δεν υπάρχουν πλέον νησίδες, επιτρέποντας καλύτερη ανάμιξη.

Με μια τομή Πουανκαρέ, η ποιότητα ανάμιξης μιας ροής μπορεί να αναλυθεί με τη διάκριση μεταξύ χαοτικών και ελλειπτικών περιοχών. Ωστόσο, αυτό είναι ένα πρόχειρο μέτρο της διαδικασίας ανάμιξης, καθώς οι ιδιότητες τάνυσης δεν μπορούν να συναχθούν από αυτή τη μέθοδο απεικόνισης. Παρά ταύτα, η τεχνική αυτή είναι πολύ χρήσιμη για τη μελέτη της ανάμιξης περιοδικών ροών και μπορεί να επεκταθεί σε τρισδιάστατο πεδίο.

Μορφοκλασματική διάσταση

Μέσα από μια συνεχή διαδικασία τεντώματος και διπλώματος, όπως σε έναν "χάρτη του αρτοποιού"... οι ιχνηθέτες που μεταφέρονται σε χαοτικές ροές θα εξελιχθούν σε πολύπλοκα φράκταλ. Η μορφοκλασματική διάσταση ενός μεμονωμένου περιγράμματος θα είναι μεταξύ 1 και 2. Η εκθετική ανάπτυξη εξασφαλίζει ότι το περίγραμμα, στο όριο των πολύ μακράς χρονικής ολοκλήρωσης, γίνεται φράκταλ. Τα φράκταλ που αποτελούνται από μία μόνο καμπύλη είναι απείρως μεγάλα και όταν σχηματίζονται επαναληπτικά, έχουν εκθετικό ρυθμό ανάπτυξης, ακριβώς όπως ένα advected contour. Η Νιφάδα του Κοχ, για παράδειγμα, αναπτύσσεται με ρυθμό 4/3 ανά επανάληψη.

Το παρακάτω σχήμα δείχνει την μορφοκλασματική διάσταση ενός περιγράμματος που μεταφέρεται ως συνάρτηση του χρόνου, μετρημένη με τέσσερις διαφορετικούς τρόπους. Μια καλή μέθοδος μέτρησης της διάστασης του φράκταλ ενός περιγράμματος που μεταδίδεται είναι ο εκθέτης αβεβαιότητας.

Εξέλιξη των πεδίων συγκέντρωσης ιχνηθετών σε χαοτική μεταφορά

Στην ανάμιξη ρευστών, συχνά επιθυμούμε να ομογενοποιήσουμε ένα είδος, το οποίο μπορεί να χαρακτηριστεί από το πεδίο συγκέντρωσης του q. Συχνά, το είδος μπορεί να θεωρηθεί ως παθητικός ιχνηθέτης που δεν τροποποιεί τη ροή. Το είδος μπορεί να είναι για παράδειγμα μια χρωστική ουσία προς ανάμιξη. Η εξέλιξη ενός πεδίου συγκέντρωσης $q$ υπακούει στην εξίσωση μεταφοράς-διάχυσης, που ονομάζεται επίσης εξίσωση συναγωγής-διάχυσης:

{\big .}{\frac {\partial q}{\partial t}}=\nabla \cdot D\nabla q-{\vec {v}}\cdot \nabla q.

Σε σύγκριση με την απλή εξίσωση διάχυσης, ο όρος που είναι ανάλογος του πεδίου ταχύτητας ${\vec {v}}$ αντιπροσωπεύει την επίδραση της συμβολής.

Κατά την ανάμιξη ενός σημείου ιχνηθέτη, ο όρος της μεταφοράς κυριαρχεί στην εξέλιξη του πεδίου συγκέντρωσης στην αρχή της διαδικασίας ανάμιξης. Η χαοτική μεταφορά μετατρέπει την κηλίδα σε δέσμη λεπτών νημάτων. Το πλάτος ενός νηματίου χρωστικής μειώνεται εκθετικά με το χρόνο, έως ότου επιτευχθεί μια κλίμακα ισορροπίας, στην οποία η επίδραση της διάχυσης αρχίζει να είναι σημαντική. Η κλίμακα αυτή ονομάζεται κλίμακα Μπάτσελορ. Ορίζεται ως η τετραγωνική ρίζα του λόγου μεταξύ του συντελεστή διάχυσης και του εκθέτη Λιαπούνοφ

w_{B}={\sqrt {\frac {D}{\lambda }}}

όπου $\lambda$ είναι ο εκθέτης Λιαπούνοφ και D είναι ο συντελεστής διάχυσης. Η κλίμακα αυτή μετρά την ισορροπία μεταξύ τάνυσης και διάχυσης στην εξέλιξη του πεδίου συγκέντρωσης: η τάνυση τείνει να μειώνει το πλάτος ενός νήματος, ενώ η διάχυση τείνει να το αυξάνει. Η κλίμακα Μπάτσελορ είναι η μικρότερη κλίμακα μήκους που μπορεί να παρατηρηθεί στο πεδίο συγκέντρωσης, δεδομένου ότι η διάχυση εξαφανίζει γρήγορα κάθε λεπτότερη λεπτομέρεια.

Όταν τα περισσότερα νημάτια χρωστικής φτάσουν στην κλίμακα Μπάτσελορ, η διάχυση αρχίζει να μειώνει σημαντικά την αντίθεση της συγκέντρωσης μεταξύ του νηματίου και της περιβάλλουσας περιοχής. Ο χρόνος κατά τον οποίο ένα νήμα φθάνει στην κλίμακα Batchelor ονομάζεται επομένως χρόνος ανάμιξης. Η ανάλυση της εξίσωσης συμβολής-διάχυσης δείχνει ότι μετά το χρόνο ανάμιξης ενός νηματίου, η μείωση της διακύμανσης της συγκέντρωσης λόγω διάχυσης είναι εκθετική, με αποτέλεσμα τη γρήγορη ομογενοποίηση με το ρευστό περιβάλλον.

Ιστορία της χαοτικής μεταφοράς

Η απαρχή της θεωρίας της χαοτικής μεταφοράς εντοπίζεται συνήθως σε μια εργασία^[4] του Χασάν Αρέφ το 1984. Στην εργασία αυτή, ο Αρέφ μελέτησε την ανάμιξη που προκαλείται από δύο δίνες που ενεργοποιούνται και απενεργοποιούνται εναλλάξ μέσα σε ένα αδιαφανές ρευστό. Αυτή η θεμελιώδης εργασία είχε καταστεί δυνατή χάρη σε προηγούμενες εξελίξεις στους τομείς των δυναμικών συστημάτων και της ρευστομηχανικής τις προηγούμενες δεκαετίες. Ο Βλάντιμιρ Άρνολντ^[8] και ο Μισέλ Χενόν^[9] είχαν ήδη παρατηρήσει ότι οι τροχιές που μεταφέρονται από τρισδιάστατες ροές που διατηρούν την περιοχή θα μπορούσαν να είναι χαοτικές. Εντούτοις, το πρακτικό ενδιαφέρον της χαοτικής συμβολής για εφαρμογές ανάμιξης ρευστών παρέμεινε απαρατήρητο έως την εργασία του Αρέφ τη δεκαετία του '80. Έκτοτε, ολόκληρη η εργαλειοθήκη των δυναμικών συστημάτων και της θεωρίας του χάους έχει χρησιμοποιηθεί για τον χαρακτηρισμό της ανάμιξης ρευστών με χαοτική συμβολή.^[1] Πρόσφατες εργασίες έχουν για παράδειγμα χρησιμοποιήσει τοπολογικές μεθόδους για να χαρακτηρίσουν την έκταση των σωματιδίων του ρευστού.^[10] Άλλες πρόσφατες κατευθύνσεις της έρευνας αφορούν τη μελέτη της χαοτικής συμβολής σε πολύπλοκες ροές, όπως οι κοκκώδεις ροές.^[11]

Βιβιογραφία

Εξωτερικοί σύνδεσμοι

ctraj: Tools for studying chaotic advection.

Δείτε επίσης

Παραπομπές

↑ ^1,0 ^1,1 J. M. Ottino (1989). The Kinematics of Mixing: Stretching, Chaos and Transport. Cambridge University Press.
↑ Aref, Hassan; Blake, John R.; Budišić, Marko; Cardoso, Silvana S. S.; Cartwright, Julyan H. E.; Clercx, Herman J. H.; El Omari, Kamal; Feudel, Ulrike και άλλοι. (2017-06-14). «Frontiers of chaotic advection». Reviews of Modern Physics 89 (2): 025007. doi:10.1103/RevModPhys.89.025007. Bibcode: 2017RvMP...89b5007A.
↑ J. Methven and B. Hoskins (1999). «The advection of high-resolution tracers by low-resolution winds». Journal of the Atmospheric Sciences 56 (18): 3262–3285. doi:10.1175/1520-0469(1999)056<3262:taohrt>2.0.co;2. Bibcode: 1999JAtS...56.3262M.
↑ ^4,0 ^4,1 Aref, H. (June 1984). «Stirring by chaotic advection». Journal of Fluid Mechanics 143: 1–21. doi:10.1017/S0022112084001233. Bibcode: 1984JFM...143....1A.
↑ ^5,0 ^5,1 ^5,2 ^5,3 Peter Mills (2004). Following the Vapour Trail: a Study of Chaotic Mixing of Water Vapour in the Upper Troposphere (PDF) (Διδακτορική διατριβή). University of Bremen. Αρχειοθετήθηκε από το πρωτότυπο (PDF) στις 21 Ιουλίου 2011. Ανακτήθηκε στις 16 Δεκεμβρίου 2010.
↑ Edward Ott (1993). Chaos in Dynamical Systems. Cambridge University Press.
↑ Arjendu K. Pattanayak (2001). «Characterizing the metastable balance between chaos and diffusion». Physica D 148 (1–2): 1–19. doi:10.1016/S0167-2789(00)00186-X. Bibcode: 2001PhyD..148....1P.
↑ Arnold, Vladimir Igorevich (1965-07-05). «Sur la topologie des écoulements stationnaires des fluides parfaits» (στα γαλλικά). Comptes rendus hebdomadaires des séances de l'Académie des Sciences (French Academy of Sciences) 261: 17–20. doi:10.1007/978-3-642-31031-7_3. ISBN 978-3-642-31030-0. ISSN 0001-4036. http://gallica.bnf.fr/ark:/12148/bpt6k4022z/f18.image.
↑ Hénon, Michel (1966-01-31). «Sur la topologie des lignes de courant dans un cas particulier» (στα γαλλικά). Comptes rendus hebdomadaires des séances de l'Académie des Sciences. A (French Academy of Sciences) 262: 312–4. ISSN 0997-4482. http://gallica.bnf.fr/ark:/12148/bpt6k6236863n/f326.image.
↑ J.-L. Thiffeault and M. D. Finn (2006). «Topology, Braids, and Mixing in Fluids». Philosophical Transactions of the Royal Society A 364 (1849): 3251–3266. doi:10.1098/rsta.2006.1899. PMID 17090458. Bibcode: 2006RSPTA.364.3251T.
↑ J.M. Ottino and D.V. Khakhar (2000). «Mixing and segregation of granular materials». Annual Review of Fluid Mechanics 32: 55–91. doi:10.1146/annurev.fluid.32.1.55. Bibcode: 2000AnRFM..32...55O.

[Ottino1989-1] 1,0 ^1,1 J. M. Ottino (1989). The Kinematics of Mixing: Stretching, Chaos and Transport. Cambridge University Press.

[2] Aref, Hassan; Blake, John R.; Budišić, Marko; Cardoso, Silvana S. S.; Cartwright, Julyan H. E.; Clercx, Herman J. H.; El Omari, Kamal; Feudel, Ulrike και άλλοι. (2017-06-14). «Frontiers of chaotic advection». Reviews of Modern Physics 89 (2): 025007. doi:10.1103/RevModPhys.89.025007. Bibcode: 2017RvMP...89b5007A.

[Methven_Hoskins1999-3] J. Methven and B. Hoskins (1999). «The advection of high-resolution tracers by low-resolution winds». Journal of the Atmospheric Sciences 56 (18): 3262–3285. doi:10.1175/1520-0469(1999)056<3262:taohrt>2.0.co;2. Bibcode: 1999JAtS...56.3262M.

[Aref1984-4] 4,0 ^4,1 Aref, H. (June 1984). «Stirring by chaotic advection». Journal of Fluid Mechanics 143: 1–21. doi:10.1017/S0022112084001233. Bibcode: 1984JFM...143....1A.

[Mills2004-5] 5,0 ^5,1 ^5,2 ^5,3 Peter Mills (2004). Following the Vapour Trail: a Study of Chaotic Mixing of Water Vapour in the Upper Troposphere (PDF) (Διδακτορική διατριβή). University of Bremen. Αρχειοθετήθηκε από το πρωτότυπο (PDF) στις 21 Ιουλίου 2011. Ανακτήθηκε στις 16 Δεκεμβρίου 2010.

[Ott1993-6] Edward Ott (1993). Chaos in Dynamical Systems. Cambridge University Press.

[Pattanayak2001-7] Arjendu K. Pattanayak (2001). «Characterizing the metastable balance between chaos and diffusion». Physica D 148 (1–2): 1–19. doi:10.1016/S0167-2789(00)00186-X. Bibcode: 2001PhyD..148....1P.

[Arnold1965-8] Arnold, Vladimir Igorevich (1965-07-05). «Sur la topologie des écoulements stationnaires des fluides parfaits» (στα γαλλικά). Comptes rendus hebdomadaires des séances de l'Académie des Sciences (French Academy of Sciences) 261: 17–20. doi:10.1007/978-3-642-31031-7_3. ISBN 978-3-642-31030-0. ISSN 0001-4036. http://gallica.bnf.fr/ark:/12148/bpt6k4022z/f18.image.

[Henon1966-9] Hénon, Michel (1966-01-31). «Sur la topologie des lignes de courant dans un cas particulier» (στα γαλλικά). Comptes rendus hebdomadaires des séances de l'Académie des Sciences. A (French Academy of Sciences) 262: 312–4. ISSN 0997-4482. http://gallica.bnf.fr/ark:/12148/bpt6k6236863n/f326.image.

[Thiffeault2006-10] J.-L. Thiffeault and M. D. Finn (2006). «Topology, Braids, and Mixing in Fluids». Philosophical Transactions of the Royal Society A 364 (1849): 3251–3266. doi:10.1098/rsta.2006.1899. PMID 17090458. Bibcode: 2006RSPTA.364.3251T.

[Ottino2000-11] J.M. Ottino and D.V. Khakhar (2000). «Mixing and segregation of granular materials». Annual Review of Fluid Mechanics 32: 55–91. doi:10.1146/annurev.fluid.32.1.55. Bibcode: 2000AnRFM..32...55O.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]