Χρήστης:Ant14/πρόχειρο
 |
Αυτή η σελίδα είναι το κύριο «πρόχειρο χρήστη» του Ant14. Ένα «πρόχειρο χρήστη» είναι υποσελίδα της προσωπικής σελίδας του χρήστη στη Βικιπαίδεια. Εξυπηρετεί ως χώρος πειραματισμών και ανάπτυξης σελίδων και δεν είναι εγκυκλοπαιδικό λήμμα. Επεξεργαστείτε ή δημιουργήστε το δικό σας πρόχειρο εδώ ή κάνετε δοκιμές στο κοινόχρηστο Πρόχειρο Βικιπαίδειας. |
Δεν πρέπει να συγχέεται με τη διάσταση μιας φυσικής ποσότητας. Για άλλες χρήσεις, δείτε Διάσταση (αποσαφήνιση).

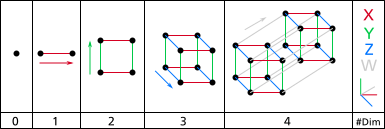
Στη φυσική και τα μαθηματικά,η διάσταση ενός χώρου ή αντικειμένου ανεπίσημα, ορίζεται ως ο ελάχιστος αριθμός των συντεταγμένων που απαιτούνται για να καθοριστεί οποιοδήποτε σημείο μέσα σε αυτό. Έτσι, μια γραμμή έχει μια διάσταση, διότι μόνο μια συντεταγμένη είναι απαραίτητη, για να προσδιορίζει ένα σημείο σχετικά με αυτό (για παράδειγμα, το σημείο 5 σε μια αριθμημένη γραμμή). Μία επιφάνεια, όπως ένα αεροπλάνο ή η επιφάνεια ενός κυλίνδρου ή σφαίρας, έχει δύο διαστάσεις, επειδή δύο συντεταγμένες χρειάζονται για να καθορίσετε ένα σημείο σε αυτό. (για παράδειγμα, για να εντοπίσετε ένα σημείο στην επιφάνεια μιας σφαίρας, θα πρέπει να έχετε τόσο το γεωγραφικό πλάτος,όσο και το γεωγραφικό μήκος του). Το εσωτερικό ενός κύβου, ενός κυλίνδρου ή σφαίρας είναι τρισδιάστατο επειδή τρεις συντεταγμένες χρειάζονται για να εντοπίσετε ένα σημείο μέσα σε αυτούς τους χώρους. Στη φυσική, διάσταση αναφέρεται στη συστατική δομή όλων των χώρων (????) και τη θέση της στο χρόνο (αντιληπτή ως μια διάσταση κατά μήκος του άξονα t), καθώς και η χωρική συγκρότηση των αντικειμένων εντός
Στη φυσική και τα μαθηματικά,η διάσταση ενός χώρου ή αντικειμένου ανεπίσημα, ορίζεται ως ο ελάχιστος αριθμός
των συντεταγμένων που απαιτούνται για να καθοριστεί οποιοδήποτε σημείο μέσα σε αυτό. Έτσι, μια γραμμή έχει
μια διάσταση, διότι μόνο μια συντεταγμένη είναι απαραίτητη, για να προσδιορίζει ένα σημείο σχετικά με αυτό (για
παράδειγμα, το σημείο 5 σε μια αριθμημένη γραμμή). Μία επιφάνεια, όπως ένα αεροπλάνο ή η επιφάνεια ενός
κυλίνδρου ή σφαίρας, έχει δύο διαστάσεις, επειδή δύο συντεταγμένες χρειάζονται για να καθορίσετε ένα σημείο
σε αυτό. (για παράδειγμα, για να εντοπίσετε ένα σημείο στην επιφάνεια μιας σφαίρας, θα πρέπει να έχετε τόσο το
γεωγραφικό πλάτος,όσο και το γεωγραφικό μήκος του). Το εσωτερικό ενός κύβου, ενός κυλίνδρου ή σφαίρας είναι
τρισδιάστατο επειδή τρεις συντεταγμένες χρειάζονται για να εντοπίσετε ένα σημείο μέσα σε αυτούς τους χώρους.
Στη φυσική, διάσταση αναφέρεται στη συστατική δομή όλων των χώρων (βλ. όγκος) και τη θέση της στο χρόνο
(αντιληπτή ως μια διάσταση κατά μήκος του άξονα t), καθώς και η χωρική συγκρότηση των αντικειμένων εντός –
δομές που σχετίζονται ταυτόχρονα με τις έννοιες των σωματιδίων και του χώρου, αλληλεπιδρούν με τις σχετικές
ιδιότητες της μάζας - και είναι βασικά σαν μαθηματικές έννοιες στην περιγραφή τους. Αυτοί, ή άλλοι άξονες μπορούν
να χρησιμοποιηθούν για να ταυτοποιήσουμε μοναδικά ένα σημείο ή δομή στη στάση του και τη σχέση του με άλλα
αντικείμενα ή μορφές. Φυσικές θεωρίες που συμπεριλαμβάνουν το χρόνο, όπως η γενική θεωρία της σχετικότητας,
θεωρούνται ότι δουλεύουν στον 4-διάστατο «χωροχρόνο» (που ορίζεται και ως χώρος Minkowski). Οι μοντέρνες
θεωρίες τείνουν να είναι «πολύ-διάστατες» και περιλαμβάνουν την θεωρία κβαντικού πεδίου και τη θεωρία των ινών.
Η δήλωση του χώρου στην κβαντομηχανική είναι ένας λειτουργικός χώρος απείρων διαστάσεων.
Η έννοια της διάστασης δεν περιορίζεται σε φυσικά αντικείμενα. Πολύ-διάστατοι χώροι υπάρχουν στα μαθηματικά
και γενικότερα στις επιστήμες για πολλούς λόγους, συχνά ως χώροι διαμόρφωσης όπως η Λαγκρανσιανή ή
Χαμιλτονιανή μηχανική; Αυτοί οι αφηρημένοι χώροι είναι ανεξάρτητοι του φυσικού χώρου στον οποίο ζούμε.
Στα μαθηματικά
[Επεξεργασία | επεξεργασία κώδικα]Στα μαθηματικά, η διάσταση ενός αντικειμένου είναι εγγενής, ανεξάρτητη ιδιοκτησία του χώρου στον οποίο το αντικείμενο είναι ενσωματωμένο. Για παράδειγμα, ένα σημείο του μοναδιαίου κύκλου στο επίπεδο μπορεί να οριστεί από δύο Καρτεσιανές συντεταγμένες, αλλά μπορεί να γίνει και μόνο με μία συντεταγμένη (την πολική συντεταγμένη γωνίας) οπότε ο κύκλος είναι μονό-διάστατος παρόλο που υπάρχει στο δι-διάστατο πεδίο. Αυτή η εγγενής κατανόηση της διάστασης από τους κυριότερους τρόπους με τους οποίους η μαθηματική έννοια της διάστασης διαφέρει από την κοινή χρήση του όρου. Η διάσταση του Ευκλείδιου n-χώρου En βρισκόμαστε αντιμέτωποι με την ερώτηση «τι κάνει το En μία πεπερασμένη μπάλα στο En η παρατήρηση μας οδηγεί στον ορισμό της διάστασης Minkowski και της πιο εξεληγμένης μορφή της, την διάσταση Hausdorff, ενώ παράλληλα υπάρχουν και άλλες πιθανές απαντήσεις στην παραπάνω ερώτηση. Για παράδειγμα, το όριο μιάς μπάλας στο En έννοιες συμφωνούν με το En Ένα κανονικό οκτά-χωρο (tesseract) είναι ένα παράδειγμα τετραδιάστατου αντικειμένου. Ενώ εκτός των μαθηματικών η έκφραση για την διάσταση είναι : «Το tesseract έχει τέσσερις διαστάσεις» στα μαθηματικά οι συνήθεις εκφράσεις είναι «Το tesseract έχει διάσταση 4» ή «Η διάσταση του tesseract είναι 4». Παρόλο που η έννοια των περισσοτέρων διαστάσεων πάει πίσω μέχρι τον Rene Deschartes, ουσιώδης εξέλιξη πάνω στην γεωμετρία πολλών διαστάσεων ξεκίνησε τον 19 Rowan Hamilton, Ludwig Schläfli και Bernhard Riemann. Το Habilitationsschrift,του Riemann το 1854,η Theorie der vielfachen Kontinuität του Schlafi το 1852, η ανακάλυψη των quaternions του Hamilton το 1843 και η κατασκευή της Cayley Algebra σηματοδότησαν την αρχή της γεωμετρίας πολλών διαστάσεων. Η υπόλοιπη ενότητα εξετάζει κάποιους από τους πιο σημαντικούς μαθηματικούς ορισμούς των διαστάσεων. είναι n. Όταν προσπαθούμε να γενικεύσουμε σε άλλων ειδών χώρους, n-διάστατο?» Μία απάντηση είναι πως για να καλύψουμε με μικρότερες μπάλες ακτίνας ε, χρειαζόμαστε στο σύστημα ε τέτοιες μπάλες. Αυτή -n μοιάζει τοπικά με Εn-1 αποδεικνύεται πως διαφοροποιούνται όταν οι χώροι γενικεύονται. και μας οδηγεί στην έννοια της επαγωγικής διάστασης. Ενώ αυτές οι αιώνα, μέσω της δουλειάς των Arthur Cayley.
Διάσταση ενός διανυσματικού χώρου
[Επεξεργασία | επεξεργασία κώδικα]Η διάσταση ενός διανυσματικού χώρου είναι ο αριθμός των διανυσμάτων σε οποιαδήποτε βάση για το χώρο, δηλαδή ο αριθμός των συντεταγμένων που είναι αναγκαίες για να διευκρινιστεί κάθε φορέας. Αυτή η έννοια της διάστασης (η πληθάριθμος της βάσης) συχνά αναφέρεται ως η Hamel διάσταση ή αλγεβρική διάσταση για να τη διακρίνουν από τις άλλες έννοιες της διάστασης. Συλλέκτες Μια πολλαπλή τοπολογική σχέση είναι τοπικά homeomorphic με την Ευκλείδειο n-χώρο, και ο αριθμός n λέγεται διάσταση του συλλέκτη. Κάποιος μπορεί να δείξει ότι αυτό δίνει έναν μοναδικό ορισμό για τη διάσταση για κάθε πολλαπλή τοπολογική σχέση. Για σχέση διαφορίσιμης πολλαπλότητας η διάσταση είναι επίσης η διάσταση της εφαπτομένης διανυσματικού διαστήματος σε οποιοδήποτε σημείο. Η θεωρία των πολλαπλοτήτων, στον τομέα της γεωμετρικής τοπολογίας, χαρακτηρίζεται από τον τρόπο με διαστάσεις 1 και 2, είναι σχετικά στοιχειώδη, οι υψηλές διαστάσεων περιπτώσεις n> 4 είναι απλοποιημένες, έχοντας επιπλέον χώρο στον οποίο να "εργάζονται". Και οι υποθέσεις n = 3 και 4 είναι, σε ορισμένες περιπτώσεις η πιο δύσκολη. Η κατάσταση αυτή ήταν ιδιαίτερα έντονη στις διάφορες περιπτώσεις του Poincaré εικασίες, όπου εφαρμόζονται τέσσερις διαφορετικές μεθόδους απόδειξης.
Πολλαπλές
[Επεξεργασία | επεξεργασία κώδικα]Μια συνδεδεμένη τοπολογική πολλαπλή είναι τοπικά homeomorphic με την Ευκλείδειο n-χώρο, και ο αριθμός n λέγεται διάσταση του συλλέκτη. Κάποιος μπορεί να δείξει ότι αυτό δίνει μια μοναδική διάσταση ορίζεται για κάθε συνδεδεμένη τοπολογική πολλαπλή.
Για συνδεδεμένες Διαφορίσιμες πολλαπλότητες η διάσταση είναι επίσης η διάσταση της εφαπτομένης διανυσματικού διαστήματος σε οποιοδήποτε σημείο.
Η θεωρία των πολλαπλοτήτων, στον τομέα της γεωμετρικής τοπολογίας, χαρακτηρίζεται από τον τρόπο με διαστάσεις 1 και 2, είναι σχετικά στοιχειώδη, οι υψηλές διαστάσεων περιπτώσεις n> 4 είναι απλοποιημένες, έχοντας επιπλέον χώρο στον οποίο να "εργάζονται". Και οι υποθέσεις n = 3 και 4 είναι, σε ορισμένες αισθήσεις η πιο δύσκολη. Η κατάσταση αυτή ήταν ιδιαίτερα έντονη στις διάφορες περιπτώσεις του Poincaré εικασίες, όπου εφαρμόζονται τέσσερις διαφορετικές μεθόδους απόδειξης.
Ποικιλίες
[Επεξεργασία | επεξεργασία κώδικα]Η διάσταση μιας αλγεβρικής ποικιλίας μπορεί να οριστεί με διάφορους ισοδύναμους τρόπους. Ο πιο έξυπνος τρόπος είναι ίσως η διάσταση της εφαπτομένης χώρου σε οποιοδήποτε κανονικό σημείο. Ένας άλλος διαισθητικός τρόπος είναι να καθοριστεί η διάσταση καθώς και ο αριθμός των υπερεπίπεδων που απαιτούνται ώστε να έχουν μια τομή με την ποικιλία που μειώνεται σε ένα πεπερασμένο αριθμό σημείων (διάσταση μηδέν). Ο ορισμός αυτός βασίζεται στο γεγονός ότι η τομή μιας ποικιλίας με ένα υπερεπίπεδο μειώνει τη διάσταση εκτός αν το υπερεπίπεδο περιέχει την ποικιλία. Ένα αλγεβρικό σύνολο είναι μια πεπερασμένη ένωση από αλγεβρικές ποικιλίες και η διάσταση είναι η μέγιστη από τις διαστάσεις των συνιστωσών του. Είναι ίση με το μέγιστο μήκος των αλυσίδων των επιμέρους ποικιλιών της συγκεκριμένης ποικιλίας (το μήκος μιας τέτοιας αλυσίδας είναι ο αριθμός των "").
Διάσταση Krull
[Επεξεργασία | επεξεργασία κώδικα]Η Krull διάσταση ενός αντιμεταθετικού δακτύλιου είναι η μέγιστη διάρκεια της αρχικής ιδέας σε αυτό. Είναι στενά συνδεδεμένη με την διάσταση μιας αλγεβρικής ποικιλίας, λόγω της φυσικής αλληλογραφίας μεταξύ των υποποικιλιών και των αρχικών ιδεών του δακτυλίου των πολυωνύμων με την ποικιλία.
Για την άλγεβρα πάνω από ένα πεδίο, η διάσταση ως διανυσματικό χώρος είναι πεπερασμένη αν και μόνο αν η Krull διάσταση της είναι μηδέν.
Κάλυψη διάστασης Lebesgue
[Επεξεργασία | επεξεργασία κώδικα]Για οποιοδήποτε κανονικό τοπολογικό διάστημα Χ, το οποίο καλύπτει Lebesgue διάσταση Χ ορίζεται να είναι n, αν n είναι ο μικρότερος ακέραιος για τον οποίο ισχύουν τα παρακάτω: κάθε ανοικτό κάλυμμα έχει μια ανοικτή τελειοποίηση (ένα δεύτερο ανοικτό κάλυμμα, όπου κάθε στοιχείο είναι ένα υποσύνολο ενός στοιχείου στο πρώτο κάλυμμα) έτσι ώστε κανένα σημείο να μην περιλαμβάνεται σε περισσότερα από n + 1 στοιχεία. Στην περίπτωση αυτή, dim X = n. Για X ενός συλλέκτη, αυτή συμπίπτει με τη διάσταση που αναφέρεται παραπάνω. Εάν δεν υπάρχει τέτοιος ακεραίος n υπάρχει, τότε η διάσταση Χ και λέγεται ότι είναι άπειρη, και γράφεται Χ = ∞. Επιπλέον, η διάσταση Χ έιναι -1, δηλαδή dim Χ = -1 αν και μόνο αν το Χ είναι άδειο. Αυτός ο ορισμός της κάλυψης διάστασης μπορεί να παραταθεί από την τάξη των κανονικών χώρων σε όλους τους χώρους Tychonoff απλώς με αντικατάσταση του όρου "ανοιχτό" στον ορισμό του όρου «λειτουργικά ανοικτή".
Επαγωγική διάσταση
[Επεξεργασία | επεξεργασία κώδικα]Ένας επαγωγικός ορισμός της διάστασης μπορεί να δημιουργηθεί ως εξής. Εξετάστε ένα διακριτό σύνολο σημείων (όπως μια πεπερασμένη συλλογή σημείων) να είναι 0-διαστάσεων. Σύροντας ένα 0-διαστάσεων αντικείμενο σε κάποια κατεύθυνση, επιτυγχάνεται ένα 1-διαστάσεων αντικείμενο. Σύροντας ένα 1-διαστάσεων αντικείμενο σε μια νέα κατεύθυνση, λαμβάνεται ένα 2-διαστάσεων αντικείμενο. Σε γενικές γραμμές λαμβάνεται ένα (n + 1) - διαστάσεων αντικείμενο με το σύρσιμο ενός n τρισδιάστατου αντικείμενου σε μία νέα κατεύθυνση. Η επαγωγική διάσταση ενός τοπολογικού χώρου μπορεί να παραπέμψει τη μικρή επαγωγική διάσταση ή τη μεγάλη επαγωγική διάσταση, και βασίζεται στην αναλογία ότι (n + 1) διαστάσεων μπάλες έχουν n διαστάσεων όρια, επιτρέποντας ένα επαγωγικό ορισμό που βασίζεται στη διάσταση των ορίων των ανοικτών συνόλων.
Hausdorff διάσταση
[Επεξεργασία | επεξεργασία κώδικα]Για δομικά πολύπλοκα σύνολα, ειδικά fractals, η διάσταση Hausdorff είναι χρήσιμη. Η διάσταση Hausdorff ορίζεται για όλους τους μετρικούς χώρους και, σε αντίθεση με τη διάσταση Hamel, Μπορούν να επιτύχουν και σε μη-ακέραιες πραγματικές τιμές. Η διάσταση κουτί ή Minkowski διάσταση είναι μια παραλλαγή της ίδιας ιδέας. Σε γενικές γραμμές, υπάρχουν περισσότεροι ορισμοί των φράκταλ διαστάσεων που εργάζονται για πολύ ακανόνιστα σύνολα και την επίτευξη των μη-ακέραιων θετικών πραγματικών τιμών. Τα fractals έχουν βρεθεί χρήσιμα για να περιγράψουν πολλά φυσικά αντικείμενα και φαινόμενα.
Χώροι Hilbert
[Επεξεργασία | επεξεργασία κώδικα]Κάθε χώρος Hilbert δέχεται μια ορθοκανονική βάση, και κάθε δύο τέτοιες βάσεις για ένα συγκεκριμένο χώρο έχουν τoν ίδιo πληθάριθμο. Αυτός ο πληθάριθμος ονομάζεται η διάσταση του χώρου Hilbert. Η διάσταση αυτή είναι πεπερασμένη αν και μόνο αν η Hamel διάσταση του χώρου είναι πεπερασμένη, και σε αυτή την περίπτωση οι παραπάνω διαστάσεις συμπίπτουν
Στη φυσική
[Επεξεργασία | επεξεργασία κώδικα]Χωρικές διαστάσεις
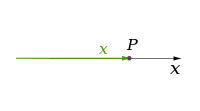
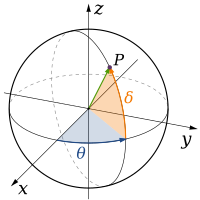
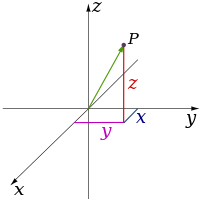
[Επεξεργασία | επεξεργασία κώδικα]Κλασσικές θεωρίες της φυσικής περιγράφουν τρεις φυσικές διαστάσεις: από ένα συγκεκριμένο σημείο στο χώρο, οι βασικές κατευθύνσεις στις οποίες μπορούμε να προχωρήσουμε είναι πάνω / κάτω, αριστερά / δεξιά και προς τα εμπρός / πίσω. Η κίνηση σε οποιαδήποτε άλλη κατεύθυνση μπορεί να εκφραστεί από την άποψη της ακριβώς αυτά τα τρία. Λίγο πιο κάτω, είναι το ίδιο που διακινούνται μέχρι αρνητική απόσταση. Μετακίνηση διαγώνια προς τα πάνω και προς τα εμπρός είναι ακριβώς όπως το όνομα της κατεύθυνσης συνεπάγεται. Δηλαδή, κινείται σε ένα γραμμικό συνδυασμό και προς τα εμπρός. Στην απλούστερη μορφή του: μια γραμμή περιγράφει μία διάσταση, ένα αεροπλάνο περιγράφει δύο διαστάσεις, και ένας κύβος περιγράφει τρεις διαστάσεις. (Βλέπε διάστημα και καρτεσιανό σύστημα συντεταγμένων.)
| Number of dimensions | Example co-ordinate systems | |||
|---|---|---|---|---|
| 1 |
| |||
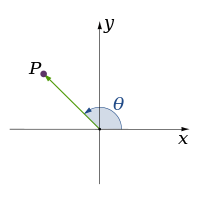
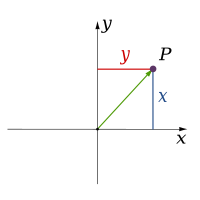
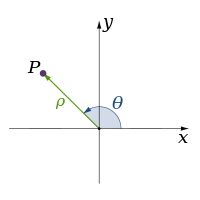
| 2 |
| |||
| 3 |
|
Χρόνος
[Επεξεργασία | επεξεργασία κώδικα]Μια χρονική διάσταση είναι η διάσταση του χρόνου. Χρόνος συχνά αναφέρεται ως "τέταρτη διάσταση" για το λόγο αυτό, αυτό δεν είναι να υπονοεί ότι είναι μια χωρική διάσταση. Μια χρονική διάσταση είναι ένας τρόπος για να μετρηθεί φυσική μεταβολή. Είναι αντιληπτό διαφορετικά από τις τρεις χωρικές διαστάσεις στο ότι υπάρχει μόνο ένα από αυτό, και ότι δεν μπορεί να κινηθεί ελεύθερα στο χρόνο, αλλά υποκειμενικά κινούνται σε μία κατεύθυνση.
Οι εξισώσεις που χρησιμοποιούνται στη φυσική στην πραγματικότητα το μοντέλο δεν αντιμετωπίζουν χρόνο με τον ίδιο τρόπο που οι άνθρωποι αντιλαμβάνονται ως συνήθως. Οι εξισώσεις της κλασικής μηχανικής είναι συμμετρικά ως προς το χρόνο, και τις εξισώσεις της κβαντικής μηχανικής είναι συνήθως συμμετρικές, αν τόσο σε χρόνο όσο και άλλες ποσότητες (όπως το φορτίο και parity) αντιστρέφονται. Σε αυτά τα μοντέλα, η αντίληψη του χρόνου που ρέει σε μια κατεύθυνση είναι ένα κατασκεύασμα των νόμων της θερμοδυναμικής (αντιλαμβανόμαστε στιγμή που ρέει προς την κατεύθυνση της αύξησης της εντροπίας).
Η πιο γνωστή αντιμετώπιση του χρόνου ως διάσταση είναι του Poincaré και η ειδική θεωρία της σχετικότητας του Αϊνστάιν (και επεκτάθηκε με τη γενική σχετικότητα), η οποία αντιμετωπίζει αντιληπτή χώρο και το χρόνο ως συστατικά τεσσάρων διαστάσεων πολλαπλή, που είναι γνωστή ως χωροχρόνου, και στην ειδική, κατ 'υπόθεση ως χώρο
Πρόσθετες διαστάσεις
[Επεξεργασία | επεξεργασία κώδικα]Στη φυσική, τρεις διαστάσεις του χώρου και μία του χρόνου είναι ο αποδεκτός κανόνας. Ωστόσο, υπάρχουν θεωρίες που προσπαθούν να ενοποιήσουν τις θεμελιώδεις δυνάμεις της με την εισαγωγή περισσότερες διαστάσεις. Η θεωρία υπερχορδών, Μ-θεωρία και θεωρία χορδής μποζονίων, αντίστοιχα, θεωρούν δεδομένο ότι ο φυσικός χώρος έχει 10, 11 και 26 διαστάσεις. Αυτές οι πρόσθετες διαστάσεις λέγεται ότι είναι χωρική. Ωστόσο, αντιλαμβανόμαστε μόνο τρεις χωρικές διαστάσεις και, μέχρι σήμερα. Μια πιθανή εξήγηση που έχει προταθεί είναι ότι ο χώρος λειτουργεί σαν να ήταν "μέχρι τα κατσαρά αντίδια" στις πρόσθετες διαστάσεις, σε υποατομικό επίπεδο, ενδεχομένως στο quark / string επίπεδο της κλίμακας ή κάτω.
Μια ανάλυση των αποτελεσμάτων από το Large Hadron Collider το Δεκέμβριο του 2010 περιορίζει σοβαρά τις θεωρίες με μεγάλες πρόσθετες διαστάσεις.
Άλλες φυσικές θεωρίες που έχουν εισαχθεί επιπλέον διαστάσεις του χώρου είναι:
- Η Kaluza-Klein θεωρία εισάγει επιπλέον διαστάσεις για να εξηγήσει τις θεμελιώδεις δυνάμεις εκτός της βαρύτητας (αρχικά μόνο ηλεκτρομαγνητισμού).
- Μεγάλη διάσταση και η Randall-Sundrum προσπαθεί για να εξηγήσει την αδυναμία της βαρύτητας. Αυτό είναι επίσης ένα χαρακτηριστικό της βράνη κοσμολογία.
- Οικουμενική επιπλέον διάσταση
Δίκτυα και διαστάσεις
[Επεξεργασία | επεξεργασία κώδικα]Μερικά σύνθετα δίκτυα χαρακτηρίζονται από fractal διαστάσεις. Η έννοια της διάστασης μπορεί να γενικευθεί σε περιλαμβάνονται δίκτυα ενσωματωμένα στο χώρο. Η διάσταση χαρακτηρίζεται ως πρός τους χωρικούς περιορισμούς της.
Λογοτεχνία
[Επεξεργασία | επεξεργασία κώδικα]Ίσως το πιο βασικό τρόπο η λέξη διάσταση χρησιμοποιείται στη λογοτεχνία σαν μια υπερβολική συνωνυμία για το χαρακτηρισμό άποψη, ή το μέγεθος. Συχνά η υπερβολή είναι αρκετά κυριολεκτική όπως ο ίδιος είναι τόσο 2-διαστάσεων, πράγμα που σημαίνει ότι μπορεί να σε κανεί να δεις με μια ματιά τι είναι. Αυτό έρχεται σε αντίθεση με 3-διάστατα αντικείμενα, τα οποία έχουν ένα εσωτερικό που είναι κρυμμένο από την άποψη, και ένα πίσω που μπορεί να φανεί μόνο με περαιτέρω εξέταση.
Τα κείμενα επιστημονικής φαντασίας συχνά αναφέρουν την έννοια της διάστασης, όταν πραγματικά αναφέρεται σε παράλληλα σύμπαντα, αναπληρωματικό σύμπαντα, ή άλλα αεροπλάνα της ύπαρξης. Αυτή η χρήση προέρχεται από την ιδέα ότι για να ταξιδέψει σε παράλληλα / εναλλακτικά σύμπαντα / αεροπλάνα της ύπαρξης πρέπει κανείς να ταξιδέψει σε μια κατεύθυνση / διάσταση, εκτός από τις τυπικές αυτές. Στην πραγματικότητα, τα άλλα σύμπαντα / αεροπλάνα είναι μόνο μια μικρή απόσταση με τα πόδια από τη δική μας, αλλά η απόσταση είναι σε ένα τέταρτο (ή υψηλότερη) χωρική (ή μη χωρικά) διάσταση, όχι οι τυπικές αυτές.
Ένα από τα πιο σημαντικές νουβέλες επιστημονικής φαντασίας σχετικά με πραγματική γεωμετρική διάσταση, και συχνά συνιστάται ως ένα σημείο εκκίνησης για εκείνους ακριβώς που αρχίζουν να ερευνήσει αυτά τα θέματα, είναι το 1884 Flatland μυθιστόρημα του Edwin A. Abbott. Isaac Asimov, στον πρόλογό του στο Signet Classics 1984 έκδοση, Flatland περιγράφεται ως «η καλύτερη εισαγωγή μπορεί κανείς να βρει στο τρόπο αντίληψης διαστάσεις."
Η ιδέα του άλλες διαστάσεις είχε ενσωματωθεί σε πολλές ιστορίες επιστημονικής φαντασίας, που εμφανίζεται, για παράδειγμα, στο Miles J. Breuer είναι το προσάρτημα και τα θεάματα (1928) και Murray Leinster είναι η πέμπτη διάσταση Καταπέλτης (1931), Και εμφανίστηκε παράνομα στην επιστήμη φαντασίας από τη δεκαετία του 1940. Κλασικές ιστορίες που αφορούν άλλες διαστάσεις έκανε και ο Robert A. Heinlein έχτισε ένα Crooked House (1941), στην οποία ένας αρχιτέκτονας Καλιφόρνια σχεδιάζει ένα σπίτι που βασίζεται σε μια τρισδιάστατη προβολή ενός tesseract, και Tiger Alan E. Nourse του από την ουρά και Το Σύμπαν μεταξύ των (δύο του 1951). Μια άλλη αναφορά είναι Madeleine L'Engle's μυθιστόρημα μια ρυτίδα In Time (1962), η οποία χρησιμοποιεί την 5η διάσταση ως ένας τρόπος για «tesseracting το σύμπαν» ή σε μια καλύτερη αίσθηση, "αναδίπλωση" χώρο για να κινηθεί πάνω σε αυτό γρήγορα. Η τέταρτη και η πέμπτη διάσταση ήταν επίσης ένα βασικό στοιχείο του βιβλίου The Boy Who ίδιος αντιστραφεί, από τον William Sleator.
Φιλοσοφία
[Επεξεργασία | επεξεργασία κώδικα]Το 1783, ο Καντ έγραψε: «Το γεγονός ότι υπάρχει παντού χώρος (το οποίο δεν είναι το το όριο κάποιου άλλου χώρου) έχει τρεις διαστάσεις και ότι ο χώρος σε γενικές γραμμές δεν μπορεί να έχει περισσότερες διαστάσεις, βασίζεται στην άποψη ότι δεν είναι περισσότερες από τρεις γραμμές αυτές που μπορούν να τέμνονται με ορθές γωνίες σε ένα σημείο. Αυτή η πρόταση δεν μπορεί καθόλου να αποδειχθεί από τις έννοιες, αλλά στηρίζεται άμεσα στη διαίσθηση και μάλιστα σε καθαρή διαίσθηση εκ των προτέρων γιατί είναι αποδεδειγμένα ορισμένες ".
Ο χώρος έχει τέσσερις διαστάσεις, είναι μια μικρή ιστορία που δημοσιεύθηκε το 1846 από τον Γερμανό φιλόσοφο και πειραματικό ψυχολόγο Gustav Fechner (με το ψευδώνυμο Δρ Mises). Ο πρωταγωνιστής της ιστορίας είναι μια σκιά που γνωρίζει και είναι σε θέση να επικοινωνεί με άλλα σκιές. Αλλά είναι παγιδευμένος σε μια δισδιάστατη επιφάνεια. Σύμφωνα με τον Fechner, ο άνθρωπος σκιά θα συλλαμβάνει την τρίτη διάσταση ως ένα χρόνο. Η ιστορία φέρει μεγάλη ομοιότητα με το «Αλληγορία του Σπηλαίου», που παρουσιάζονται σε Πλάτωνος Η Δημοκρατία γράφτηκε γύρω στο 380 π.Χ.
Ο Simon Newcomb έγραψε ένα άρθρο για το Δελτίο της Αμερικανικής Μαθηματικής Εταιρείας το 1898 με τίτλο «Η Φιλοσοφία της υπερδιάστημα». Η Linda Dalrymple Henderson επινόησε τον όρο φιλοσοφία Hyperspace το 1983 διατριβή της για την τέταρτη διάσταση στις αρχές του εικοστού αιώνα, την τέχνη. Αυτή χρησιμοποιείται για να περιγράψει εκείνες τις συγγραφείς που χρησιμοποιούν υψηλότερες διαστάσεις για μεταφυσική και φιλοσοφική έρευνα. Ο Charles Howard Hinton (ο οποίος ήταν ο πρώτος που χρησιμοποίησε τη λέξη "tesseract" το 1888) και το ρωσικό esotericist Π.Δ. Ουσπένσκυ είναι παραδείγματα του "φιλοσόφων υπερδιάστημα ".
Further reading
[Επεξεργασία | επεξεργασία κώδικα]- Edwin A. Abbott, (1884) Flatland: A Romance of Many Dimensions, Public Domain. Online version with ASCII approximation of illustrations at Project Gutenberg.
- Thomas Banchoff, (1996) Beyond the Third Dimension: Geometry, Computer Graphics, and Higher Dimensions, Second Edition, Freeman.
- Clifford A. Pickover, (1999) Surfing through Hyperspace: Understanding Higher Universes in Six Easy Lessons, Oxford University Press.
- Rudy Rucker, (1984) The Fourth Dimension, Houghton-Mifflin.
- Michio Kaku, (1994) Hyperspace, a Scientific Odyssey Through the 10th Dimension, Oxford University Press.
External links
[Επεξεργασία | επεξεργασία κώδικα]- Copeland, Ed (2009). «Extra Dimensions». Sixty Symbols. Brady Haran for the University of Nottingham.