Βαρυτόνιο
| Το λήμμα δεν περιέχει πηγές ή αυτές που περιέχει δεν επαρκούν. |
| Σύνθεση | Στοιχειώδες σωμάτιο |
|---|---|
| Στατιστική | Μποζονική |
| Αλληλεπιδράσεις | Βαρυτική |
| Σύμβολο | G [Σημ. 1] |
| Προβλέφθηκε θεωρητικά | Τη δεκαετία του 1930[1] Το όνομα αποδίδεται στους Dmitrii Blokhintsev και F. M. Gal'perin το 1934[2] |
| Ανακαλύφθηκε | Υποθετικό σωμάτιο |
| Αναλλοίωτη μάζα | 0 |
| Μέσος χρόνος ζωής | Σταθερό |
| Ηλεκτρικό φορτίο | 0 |
| Σπιν | 2 |
Στην φυσική, το βαρυτόνιο (ή αλλιώς γκραβιτόνιο από τον αγγλικό όρο graviton) είναι το υποθετικό στοιχειώδες σωματίδιο-φορέας της βαρυτικής αλληλεπίδρασης και προβλέπεται στα πλαίσια ενός ολοκληρωμένου και συνεπούς θεωρητικού οικοδομήματος το οποίο θα περιλαμβάνει τη βαρύτητα σε κβαντισμένη μορφή[3]:Problem 12.16 (Κβαντική βαρύτητα). Σύμφωνα με αυτή την διατύπωση, η βαρυτική αλληλεπίδραση μεταδίδεται μέσω βαρυτονίων και παύει να είναι καμπυλώσεις του χωροχρονικού συνεχούς. Προϋπόθεση και περιορισμός είναι πως, στο κλασσικό όριο, και οι δύο τρόποι πρέπει να παράγουν ταυτόσημα αποτελέσματα.
Το βαρυτόνιο ουσιαστικά αντιπροσωπεύει το κβάντο[4][5] της βαρυτικής ακτινοβολίας υπό μορφή βαρυτικών κυμάτων όπως αυτά προβλέπονται από την Γενική Σχετικότητα[6][7]. Η ύπαρξή του δε είναι "αναγκαστική" μετά τον επιτυχή κβαντισμό των υπόλοιπων τριών θεμελιωδών αλληλεπιδράσεων σε θεωρητικό επίπεδο και την πειραματική τους επαλήθευση.
Εάν υπάρχει, το βαρυτόνιο πρέπει να έχει μηδενική μάζα ηρεμίας (απαραίτητη για την άπειρη ακτίνα δράσης της βαρυτικής αλληλεπίδρασης) και να είναι μποζόνιο με σπιν (spin) ίσο με 2[8] καθώς, στα πλαίσια της Γενικής Σχετικότητας, η βαρύτητα παρουσιάζεται ως τανυστής πεδίου δεύτερης βαθμίδας. Επίσης, το βαρυτόνιο πρέπει να είναι ηλεκτρικά ουδέτερο. Στα πλαίσια της υπερσυμμετρίας το υπερβαρυτικό φερμιόνιο, το βαρυτίνο (gravitino), έχει σπιν 3/2.
Ενώ γίνονται προσπάθειες σε αρκετές μορφές κβαντικής βαρύτητας, η Θεωρία Χορδών είναι εκείνη που προβλέπει την ύπαρξη του βαρυτονίου και ταυτόχρονα διατυπώνει με ικανοποιητική σαφήνεια τις αλληλεπιδράσεις του. Στην διαταρακτική (perturbative) διατύπωση της θεωρίας Χορδών, το βαρυτόνιο περιγράφεται ως μια κλειστή χορδή με συγκεκριμένη κατάσταση ταλάντωσης πολύ χαμηλής ενέργειας. Μια ολοκληρωμένη μη διαταρακτική (non-perturbative) διατύπωση του βαρυτονίου δεν έχει καταστεί δυνατή, όπως άλλωστε και με τα περισσότερα στοχεία της θεωρίας Χορδών.
Προγράμματα για την εξακρίβωση της ύπαρξης των βαρυτονίων μέσω έμμεσων παρατηρήσεων, όπως πειράματα στοχεύοντας στην παρατήρηση και ανίχνευση βαρυτικών κυμάτων με τους ανιχνευτές LIGO, VIRGO, GEO 600 και TAMA 300, είναι σε λειτουργία. Επίσης πειράματα Φυσικής υψηλών ενεργειών στον νέο επιταχυντή LHC του CERN θα προσπαθήσουν να δώσουν απαντήσεις για την ύπαρξη (ή όχι) των βαρυτονίων και κατά συνέπεια των επιπλέον διαστάσεων (extra dimensions) όπως προβλέπουν οι θεωρίες Χορδών.
-
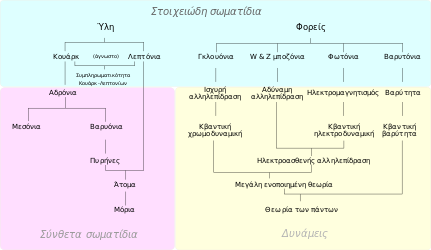
Σύνοψη των σωματιδίων και των δυνάμεων της σωματιδιακής φυσικής
Σημειώσεις
[Επεξεργασία | επεξεργασία κώδικα]Παραπομπές
[Επεξεργασία | επεξεργασία κώδικα]- ↑ Rovelli, C. (2001). «Notes for a brief history of quantum gravity». .
- ↑ Blokhintsev, D. I.; Gal'perin, F. M. (1934). «Gipoteza neitrino i zakon sokhraneniya energii [Neutrino hypothesis and conservation of energy]». Pod Znamenem Marxisma 6: 147–157. (Ρωσικά)
- ↑ Lightman, A. P.· Press, W. H.· Price, R. H.· Teukolsky, S. A. (1975). Problem book in Relativity and Gravitation. Princeton University Press. ISBN 0-691-08162-X.
- ↑ Wiener, N. (1966). Differential Space, Quantum Systems, and Prediction. Cambridge: The Massachusetts Institute of Technology Press
- ↑ E. Cobham Brewer 1810–1897. Dictionary of Phrase and Fable. 1898
- ↑ Einstein, A (June 1916). "Näherungsweise Integration der Feldgleichungen der Gravitation". Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften Berlin. part 1: 688–696
- ↑ Einstein, A (1918). "Über Gravitationswellen". Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften Berlin. part 1: 154–167
- ↑ For a comparison of the geometric derivation and the (non-geometric) spin-2 field derivation of general relativity, refer to box 18.1 (and also 17.2.5) of Misner, C. W.· Thorne, K. S.· Wheeler, J. A. (1973). Gravitation. W. H. Freeman. ISBN 0-7167-0344-0.
Εξωτερικοί σύνδεσμοι
[Επεξεργασία | επεξεργασία κώδικα]
| Αυτό το λήμμα σχετικά με τη Φυσική χρειάζεται επέκταση. Μπορείτε να βοηθήσετε την Βικιπαίδεια επεκτείνοντάς το. |