Μετάβαση στο περιεχόμενο

Θεωρία των μοριακών τροχιακών

Από τη Βικιπαίδεια, την ελεύθερη εγκυκλοπαίδεια
Δείτε επίσης: Μοριακό τροχιακό

Στη χημεία, η θεωρία των μοριακών τροχιακών (θεωρία MO ή (molecular orbital theory, MOT)) είναι μια μέθοδος για την περιγραφή της ηλεκτρονικής δομής των μορίων χρησιμοποιώντας κβαντική μηχανική. Προτάθηκε στις αρχές του 20ου αιώνα Στη θεωρία των μοριακών τροχιακών, τα ηλεκτρόνια σε ένα μόριο δεν αποδίδονται σε μεμονωμένους χημικούς δεσμούς μεταξύ ατόμων, αλλά αντιμετωπίζονται ως κινούμενα υπό την επίδραση των ατομικών πυρήνων σε ολόκληρο το μόριο.[1] Η κβαντομηχανική περιγράφει τις χωρικές και ενεργειακές ιδιότητες των ηλεκτρονίων ως μοριακά τροχιακά που περιβάλλουν δύο ή περισσότερα άτομα σε ένα μόριο και περιέχουν ηλεκτρόνια σθένους μεταξύ των ατόμων. Η θεωρία των μοριακών τροχιακών έφερε επανάσταση στη μελέτη των χημικών δεσμών προσεγγίζοντας τις καταστάσεις των δεσμικών ηλεκτρονίων—τα μοριακά τροχιακά—ως γραμμικούς συνδυασμούς ατομικών τροχιακών (linear combinations of atomic orbitals, LCAO). Αυτές οι προσεγγίσεις γίνονται εφαρμόζοντας τα πρότυπα της θεωρίας συναρτησιακής πυκνότητας (density functional theory, DFT) ή τη μέθοδο Hartree–Fock (Hartree–Fock method, HF) στην εξίσωση Schrödinger. Η θεωρία των μοριακών τροχιακών και η θεωρία του δεσμού σθένους είναι οι θεμελιώδεις θεωρίες της κβαντικής χημείας.

Μέθοδος γραμμικού συνδυασμού ατομικών τροχιακών (LCAO).

[Επεξεργασία | επεξεργασία κώδικα]

Με τη μέθοδο LCAO, κάθε μόριο έχει ένα σύνολο από μοριακά τροχιακά. Υποτίθεται ότι η κυματοσυνάρτηση ψj του μοριακού τροχιακού μπορεί να γραφτεί ως ένα απλό σταθμισμένο άθροισμα του n συστατικού των ατομικών τροχιακών χi, σύμφωνα με την ακόλουθη εξίσωση:[2] Κάποιος μπορεί να προσδιορίσει τους συντελεστές cij αριθμητικά αντικαθιστώντας αυτήν την εξίσωση στην εξίσωση Schrödinger και εφαρμόζοντας την αρχή της μεταβλητότητας. Η αρχή της μεταβλητότητας είναι μια μαθηματική τεχνική που χρησιμοποιείται στην κβαντομηχανική για τη δημιουργία των συντελεστών κάθε ατομικής τροχιακής βάσης. Ένας μεγαλύτερος συντελεστής σημαίνει ότι η τροχιακή βάση αποτελείται περισσότερο από αυτό το συνεισφέρον ατομικό τροχιακό - επομένως, το μοριακό τροχιακό χαρακτηρίζεται καλύτερα από αυτόν τον τύπο. Αυτή η μέθοδος ποσοτικοποίησης της τροχιακής συμβολής ως γραμμικός συνδυασμός ατομικών τροχιακών χρησιμοποιείται στην υπολογιστική χημεία. Ένας επιπλέον ενιαίος μετασχηματισμός (unitary transformation) μπορεί να εφαρμοστεί στο σύστημα για να επιταχυνθεί η σύγκλιση σε ορισμένα υπολογιστικά σχήματα. Η θεωρία των μοριακών τροχιακών θεωρήθηκε ως ανταγωνιστής της θεωρίας του δεσμού σθένους στη δεκαετία του 1930, πριν γίνει αντιληπτό ότι οι δύο μέθοδοι συνδέονται στενά και ότι όταν επεκταθούν γίνονται ισοδύναμες. Η θεωρία των μοριακών τροχιακών χρησιμοποιείται για την ερμηνεία της φασματοσκοπίας υπεριώδους-ορατού (UV-VIS). Οι αλλαγές στην ηλεκτρονική δομή των μορίων μπορούν να φανούν από την απορρόφηση του φωτός σε συγκεκριμένα μήκη κύματος. Μπορούν να γίνουν αντιστοιχίσεις σε αυτά τα σήματα που υποδεικνύονται από τη μετάβαση ηλεκτρονίων που κινούνται από ένα τροχιακό με χαμηλότερη ενέργεια σε ένα τροχιακό υψηλότερης ενέργειας. Το διάγραμμα του μοριακού τροχιακού για την τελική κατάσταση περιγράφει την ηλεκτρονική φύση του μορίου σε διεγερμένη κατάσταση. Υπάρχουν τρεις βασικές απαιτήσεις για να είναι κατάλληλοι οι συνδυασμοί των ατομικών τροχιακών ως προσεγγιστικά μοριακά τροχιακά.

  1. Ο συνδυασμός ατομικών τροχιακών πρέπει να έχει τη σωστή συμμετρία, που σημαίνει ότι πρέπει να ανήκει στη σωστή μη αναγώγιμη αναπαράσταση (irreducible representation) της ομάδας μοριακής συμμετρίας (molecular symmetry group). Χρησιμοποιώντας γραμμικούς συνδυασμούς προσαρμοσμένους στη συμμετρία (symmetry adapted linear combinations, SALC) μπορούν να σχηματιστούν μοριακά τροχιακά της σωστής συμμετρίας.
  2. Τα ατομικά τροχιακά πρέπει επίσης να επικαλύπτονται μέσα στο χώρο. Δεν μπορούν να συνδυαστούν για να σχηματίσουν μοριακά τροχιακά εάν είναι πολύ μακριά το ένα από το άλλο.
  3. Τα ατομικά τροχιακά πρέπει να βρίσκονται σε παρόμοια ενεργειακά επίπεδα για να συνδυαστούν με τα μοριακά τροχιακά. Γιατί εάν η διαφορά ενέργειας είναι μεγάλη, όταν σχηματίζονται τα μοριακά τροχιακά, η μεταβολή της ενέργειας γίνεται μικρή. Κατά συνέπεια, δεν υπάρχει αρκετή μείωση της ενέργειας των ηλεκτρονίων για να γίνει σημαντικός δεσμός.[3]

Ιστορικό

[Επεξεργασία | επεξεργασία κώδικα]

Η θεωρία των μοριακών τροχιακών αναπτύχθηκε τα χρόνια μετά την καθιέρωση της θεωρίας του δεσμού σθένους (1927), κυρίως μέσω των προσπαθειών των Friedrich Hund, Ρόμπερτ Μιούλικεν, John C. Slater και John Lennard-Jones.[4] Η θεωρία μοριακών τροχιακών ονομαζόταν αρχικά θεωρία Hund-Mulliken.[5] Σύμφωνα με τον φυσικό και φυσικοχημικό Erich Hückel, η πρώτη ποσοτική χρήση της θεωρίας των μοριακών τροχιακών ήταν η εργασία του Lennard-Jones, το 1929.[6][7] Αυτή η εργασία προέβλεψε μια τριπλή θεμελιώδη κατάσταση για το οξυγόνο απλής κατάστασης που εξηγούσε τον παραμαγνητισμό του[8][9] Η λέξη «τροχιακό» εισήχθη από τον Mulliken το 1932.[5] Μέχρι το 1933, η θεωρία των μοριακών τροχιακών είχε γίνει αποδεκτή ως έγκυρη και χρήσιμη θεωρία.[10] Ο Erich Hückel εφάρμοσε τη μοριακή τροχιακή θεωρία σε μόρια ακόρεστων υδρογονανθράκων ξεκινώντας το 1931 με τη μέθοδο Hückel μοριακού τροχιακού (Hückel molecular orbital, HMO) για τον προσδιορισμό των ενεργειών MO για π ηλεκτρόνια, την οποία εφάρμοσε σε συζευγμένους και αρωματικούς υδρογονάνθρακες.[11][12] Αυτή η μέθοδος παρείχε μια εξήγηση της σταθερότητας των μορίων με έξι πι-ηλεκτρόνια όπως το βενζόλιο. Ο πρώτος ακριβής υπολογισμός μιας μοριακής τροχιακής κυματοσυνάρτησης ήταν αυτός που έκανε ο Charles Coulson το 1938 σχετικά με το μόριο του υδρογόνου.[13] Μέχρι το 1950, τα μοριακά τροχιακά ορίστηκαν πλήρως ως ιδιοσυναρτήσεις (κυματικές συναρτήσεις) του αυτοσυνεπούς χαμιλτονιανού πεδίου και ήταν σε αυτό το σημείο που η μοριακή τροχιακή θεωρία έγινε πλήρως αυστηρή και συνεπής .[14] Αυτή η αυστηρή προσέγγιση είναι γνωστή ως μέθοδος Hartree–Fock για τα μόρια, αν και είχε τις ρίζες της στους υπολογισμούς των ατόμων. Στους υπολογισμούς σε μόρια, τα μοριακά τροχιακά επεκτείνονται ως προς ένα ατομικό τροχιακό σύνολο βάσης, που οδηγεί στις εξισώσεις Roothaan.[15] Αυτό οδήγησε στην ανάπτυξη πολλών μεθόδων κβαντικής χημείας εξ αρχής. Παράλληλα, η θεωρία των μοριακών τροχιακών εφαρμόστηκε με πιο προσεγγιστικό τρόπο χρησιμοποιώντας ορισμένες εμπειρικά προερχόμενες παραμέτρους σε μεθόδους που είναι τώρα γνωστές ως ημιεμπειρικές μέθοδοι κβαντικής χημείας.[15] Η επιτυχία της θεωρίας των μοριακών τροχιακών προκάλεσε επίσης τη θεωρία πεδίου προσδέματος (ligand field theory), η οποία αναπτύχθηκε κατά τις δεκαετίες του 1930 και του 1940 ως εναλλακτική λύση στη θεωρία πεδίου κρυστάλλου (crystal field theory).

Τύποι τροχιακών

[Επεξεργασία | επεξεργασία κώδικα]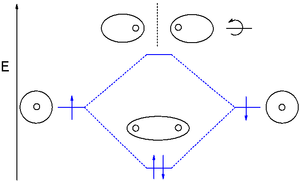
Διάγραμμα μοριακών τροχιακών (MO) που δείχνει τον σχηματισμό μοριακών τροχιακών του H2 (κέντρο) από ατομικά τροχιακά δύο ατόμων Η. Το MO χαμηλότερης ενέργειας συνδέεται με την πυκνότητα ηλεκτρονίων συγκεντρωμένη μεταξύ των δύο πυρήνων Η. Το MO υψηλότερης ενέργειας είναι αντιδεσμικό με πυκνότητα ηλεκτρονίων συγκεντρωμένη πίσω από κάθε πυρήνα Η.

Η θεωρία των μοριακών τροχιακών (MO) χρησιμοποιεί έναν γραμμικό συνδυασμό ατομικών τροχιακών (linear combination of atomic orbitals, LCAO) για να αναπαραστήσει τα μοριακά τροχιακά που προκύπτουν από δεσμούς μεταξύ ατόμων. Αυτά συχνά χωρίζονται σε τρεις τύπους, δεσμός (bonding), αντιδεσμός (antibonding) και μη δεσμός (non-bonding). Ένα δεσμικό τροχιακό συγκεντρώνει την πυκνότητα ηλεκτρονίων στην περιοχή «μεταξύ» ενός δεδομένου ζεύγους ατόμων, έτσι ώστε η πυκνότητα ηλεκτρονίων του να τείνει να έλκει τον καθένα από τους δύο πυρήνες προς τον άλλο και να συγκρατεί τα δύο άτομα μαζί.[16] Ένα αντιδεσμικό τροχιακό συγκεντρώνει την πυκνότητα ηλεκτρονίων «πίσω» από κάθε πυρήνα (δηλαδή στην πλευρά κάθε ατόμου που είναι πιο μακριά από το άλλο άτομο) και έτσι τείνει να τραβήξει κάθε έναν από τους δύο πυρήνες μακριά από τον άλλο και στην πραγματικότητα να αποδυναμώσει τον δεσμό μεταξύ των δύο πυρήνων. Τα ηλεκτρόνια σε μη δεσμικά τροχιακά τείνουν να συνδέονται με ατομικά τροχιακά που δεν αλληλεπιδρούν θετικά ή αρνητικά μεταξύ τους και τα ηλεκτρόνια σε αυτά τα τροχιακά ούτε συμβάλλουν ούτε μειώνουν την αντοχή του δεσμού.[16] Τα μοριακά τροχιακά χωρίζονται περαιτέρω ανάλογα με τους τύπους των ατομικών τροχιακών από τα οποία σχηματίζονται. Οι χημικές ουσίες θα σχηματίσουν αλληλεπιδράσεις δεσμού, εάν τα τροχιακά τους γίνουν χαμηλότερα σε ενέργεια, όταν αλληλεπιδρούν μεταξύ τους. Διακρίνονται διαφορετικά τροχιακά δεσμού που διαφέρουν κατά τη ηλεκτρονική δομή (σχήμα νέφους ηλεκτρονίων) και κατά τα ενεργειακά επίπεδα. Τα μοριακά τροχιακά ενός μορίου μπορούν να απεικονιστούν σε μοριακά τροχιακά διαγράμματα. Τα συνηθισμένα τροχιακά δεσμού είναι τα σ τροχιακά που είναι συμμετρικά ως προς τον άξονα του δεσμού και τα π τροχιακά με ένα κομβικό επίπεδο κατά μήκος τον άξονα του δεσμού. Λιγότερο κοινά είναι τα δ τροχιακά και φ τροχιακά με δύο και τρία κομβικά επίπεδα αντίστοιχα κατά μήκος του άξονα του δεσμού. Τα αντιδεσμικά τροχιακά δηλώνονται με την προσθήκη ενός αστερίσκου. Για παράδειγμα, ένα αντιδεσμικό τροχιακό pi μπορεί να εμφανίζεται ως π*.

Τάξη δεσμού

[Επεξεργασία | επεξεργασία κώδικα]
Μοριακό τροχιακό διάγραμμα του He2

Τάξη δεσμού είναι ο αριθμός των χημικών δεσμών μεταξύ ενός ζεύγους ατόμων. Η τάξη δεσμού ενός μορίου μπορεί να υπολογιστεί αφαιρώντας τον αριθμό των ηλεκτρονίων στα αντιδεσμικά τροχιακά από τον αριθμό των δεσμικών τροχιακών και ο αριθμός που προκύπτει διαιρείται στη συνέχεια με δύο. Ένα μόριο αναμένεται να είναι σταθερό εάν έχει τάξη δεσμού μεγαλύτερη από το μηδέν. Είναι επαρκές να ληφθεί υπόψη το ηλεκτρόνιο σθένους για να προσδιοριστεί η τάξη του δεσμού. Διότι (με κύριο κβαντικό αριθμό, n>1) όταν τα μοριακά τροχιακά προέρχονται από 1s ατομικά τροχιακά, η διαφορά στον αριθμό των ηλεκτρονίων στο δεσμικό και στο αντιδεσμικό μοριακό τροχιακό είναι μηδέν. Άρα, δεν υπάρχει καθαρή επίδραση στη τάξη δεσμού εάν το ηλεκτρόνιο δεν είναι το σθένος. Τάξη δεσμού = 1/2 [(Αριθμός ηλεκτρονίων στα δεσμικά μοριακά) - (Αριθμός των ηλεκτρονίων σε αντιδεσμικά μοριακά τροχιακά)]. Από τη τάξη δεσμού, μπορεί κανείς να προβλέψει εάν ένας δεσμός μεταξύ δύο ατόμων θα σχηματιστεί ή όχι. Για παράδειγμα, η ύπαρξη του μορίου He2. Από το μοριακό τροχιακό διάγραμμα, η τάξη δεσμού=1/2*(2-2)=0. Αυτό σημαίνει ότι δεν θα συμβεί κανένας σχηματισμός δεσμού μεταξύ δύο ατόμων He που φαίνεται πειραματικά. Μπορεί να ανιχνευθεί κάτω από μοριακή δέσμη πολύ χαμηλής θερμοκρασίας και πίεσης και έχει ενέργεια δέσμευσης (binding energy) περίπου 0,001 J/mol.[3] Εξάλλου, η ισχύς ενός δεσμού μπορεί να γίνει αντιληπτή και από την τάξη δεσμού (BO). Παραδείγματος χάρη: H2 :BO=(2-0)/2=1; Ενέργεια δεσμού= 436 kJ/mol. H2+ :BO=(1-0)/2=1/2; Ενέργεια δεσμού =171 kJ/mol. Καθώς η τάξη δεσμού του H2+ είναι μικρότερη από την αντίστοιχη του H2, θα πρέπει να είναι λιγότερο σταθερή, κάτι που παρατηρείται πειραματικά και μπορεί να φανεί από την ενέργεια δεσμού.

Επισκόπηση

[Επεξεργασία | επεξεργασία κώδικα]

Η θεωρία μοριακών τροχιακών παρέχει μια γενική, απεντοπισμένη προοπτική για τον χημικό δεσμό. Στη θεωρία μοριακών τροχιακών, «οποιοδήποτε» ηλεκτρόνιο σε ένα μόριο μπορεί να βρεθεί «οπουδήποτε» στο μόριο, καθώς οι κβαντικές συνθήκες επιτρέπουν στα ηλεκτρόνια να ταξιδεύουν υπό την επίδραση ενός αυθαίρετα μεγάλου αριθμού πυρήνων, εφόσον βρίσκονται σε επιτρεπόμενες ιδιοκαταστάσεις από ορισμένους κβαντικούς κανόνες. Έτσι, όταν διεγείρονται με την απαιτούμενη ποσότητα ενέργειας μέσω φωτός υψηλής συχνότητας ή άλλων μέσων, τα ηλεκτρόνια μπορούν να μεταβούν σε μοριακά τροχιακά υψηλότερης ενέργειας. Παραδείγματος χάρη, στην απλή περίπτωση ενός διατομικού μορίου υδρογόνου, η προώθηση ενός μόνο ηλεκτρονίου από ένα δεσμικό τροχιακό σε ένα αντιδεσμικό τροχιακό μπορεί να συμβεί κάτω από ακτινοβολία υπεριώδους. Αυτή η προώθηση αποδυναμώνει τον δεσμό μεταξύ των δύο ατόμων υδρογόνου και μπορεί να οδηγήσει σε φωτοδιάσπαση—το σπάσιμο ενός χημικού δεσμού λόγω της απορρόφησης φωτός. Η θεωρία μοριακών τροχιακών χρησιμοποιείται για την ερμηνεία της φασματοσκοπίας υπεριώδους-ορατής (UV-VIS). Οι αλλαγές στην ηλεκτρονική δομή των μορίων μπορούν να φανούν από την απορρόφηση του φωτός σε συγκεκριμένα μήκη κύματος. Μπορούν να γίνουν αντιστοιχίσεις σε αυτά τα σήματα που υποδεικνύονται από τη μετάβαση ηλεκτρονίων που κινούνται από ένα τροχιακό με χαμηλότερη ενέργεια σε ένα τροχιακό υψηλότερης ενέργειας. Το μοριακό τροχιακό διάγραμμα για την τελική κατάσταση περιγράφει την ηλεκτρονική φύση του μορίου σε διεγερμένη κατάσταση. Αν και στη θεωρία των μοριακών τροχιακών «μερικά» μοριακά τροχιακά μπορεί να συγκρατούν ηλεκτρόνια που είναι πιο εντοπισμένα μεταξύ συγκεκριμένων ζευγών μοριακών ατόμων, «άλλα» τροχιακά μπορεί να συγκρατούν ηλεκτρόνια που είναι πιο ομοιόμορφα διασκορπισμένα στο μόριο. Έτσι, συνολικά, ο δεσμός είναι πολύ πιο απεντοπισμένος στη θεωρία μοριακών τροχιακών, γεγονός που τον καθιστά πιο εφαρμόσιμο σε συντονισμένα μόρια που έχουν ισοδύναμες τάξεις μη ακέραιων δεσμών από τη θεωρία δεσμού σθένους. Αυτό κάνει τη θεωρία μοριακών τροχιακών πιο χρήσιμη για την περιγραφή των εκτεταμένων συστημάτων.

Ο Ρόμπερτ Μιούλικεν, ο οποίος συμμετείχε ενεργά στην εμφάνιση της μοριακής θεωρίας των τροχιακών, θεωρεί κάθε μόριο ως μια αυτάρκη μονάδα. Ο ίδιος υποστηρίζει στο άρθρο του:

... Οι προσπάθειες να θεωρηθεί ένα μόριο ως αποτελούμενο από συγκεκριμένες ατομικές ή ιοντικές μονάδες που συγκρατούνται μεταξύ τους από διακριτούς αριθμούς δεσμικών ηλεκτρονίων ή ζευγών ηλεκτρονίων θεωρούνται λίγο πολύ άνευ σημασίας, εκτός από μια προσέγγιση σε ειδικές περιπτώσεις ή ως μέθοδος υπολογισμού […] . Ένα μόριο θεωρείται εδώ ως ένα σύνολο πυρήνων, γύρω από κάθε έναν από τους οποίους ομαδοποιείται μια διάταξη ηλεκτρονίων πολύ παρόμοια με αυτή ενός ελεύθερου ατόμου σε ένα εξωτερικό πεδίο, με τη διαφορά ότι τα εξωτερικά μέρη των διαμορφώσεων ηλεκτρονίων που περιβάλλουν κάθε πυρήνα ανήκουν συνήθως, εν μέρει , από κοινού σε δύο ή περισσότερους πυρήνες....[17]

Ένα παράδειγμα είναι η περιγραφή των μοριακών τροχιών του βενζολίου, C6H6, που είναι ένας αρωματικός εξαγωνικός δακτύλιος έξι ατόμων άνθρακα και τριών διπλών δεσμών. Σε αυτό το μόριο, 24 από τα 30 συνολικά ηλεκτρόνια δεσμικού σθένους—24 προέρχονται από άτομα άνθρακα και 6 από άτομα υδρογόνου—βρίσκονται σε 12 δεσμικά τροχιακά σ, τα οποία βρίσκονται κυρίως μεταξύ ζευγών ατόμων (C-C ή C-H), παρόμοια με τα ηλεκτρόνια στην περιγραφή του δεσμού σθένους. Ωστόσο, στο βενζόλιο τα υπόλοιπα έξι δεσμικά ηλεκτρόνια βρίσκονται σε τρία τροχιακά μοριακού δεσμού π που είναι απεντοπισμένα γύρω από τον δακτύλιο. Δύο από αυτά τα ηλεκτρόνια βρίσκονται σε ένα μοριακό τροχιακό που έχει ίσες τροχιακές συνεισφορές και από τα έξι άτομα. Τα άλλα τέσσερα ηλεκτρόνια βρίσκονται σε τροχιακά με κάθετους κόμβους σε ορθή γωνία μεταξύ τους. Όπως και στη θεωρία δεσμών σθένους, και τα έξι απεντοπισμένα π ηλεκτρόνια βρίσκονται σε έναν μεγαλύτερο χώρο που υπάρχει πάνω και κάτω από το επίπεδο του δακτυλίου. Όλοι οι δεσμοί άνθρακα-άνθρακα στο βενζόλιο είναι χημικά ισοδύναμοι. Στη θεωρία των μοριακών τροχιακών αυτό είναι άμεση συνέπεια του γεγονότος ότι τα τρία μοριακά τροχιακά π συνδυάζουν και κατανέμουν ομοιόμορφα τα επιπλέον έξι ηλεκτρόνια σε έξι άτομα άνθρακα.

Δομή του βενζολίου

Σε μόρια όπως το μεθάνιο, CH4, τα οκτώ ηλεκτρόνια σθένους βρίσκονται σε τέσσερα μοριακά τροχιακά που είναι απλωμένα και στα πέντε άτομα. Είναι δυνατός ο μετασχηματισμός των μοριακών τροχιακών σε τέσσερα εντοπισμένα sp3 τροχιακά. Ο Linus Pauling, το 1931, υβριδοποίησε τα τροχιακά άνθρακα 2s και 2p έτσι ώστε να δείχνουν απευθείας τις συναρτήσεις βάσεις του υδρογόνου 1s και να έχουν τη μέγιστη επικάλυψη. Ωστόσο, η περιγραφή του απεντοπισμένου μοριακού τροχιακού είναι πιο κατάλληλη για την πρόβλεψη των ενεργειών ιονισμού και των θέσεων των φασματικών ζωνών απορρόφησης. Όταν το μεθάνιο ιονίζεται, ένα μόνο ηλεκτρόνιο λαμβάνεται από τα μοριακά τροχιακά σθένους, τα οποία μπορεί να προέρχονται από τον δεσμό s ή τα τριπλά εκφυλισμένα επίπεδα δεσμού p, αποδίδοντας δύο ενέργειες ιονισμού. Συγκριτικά, η εξήγηση στη θεωρία δεσμού σθένους είναι πιο περίπλοκη. Όταν ένα ηλεκτρόνιο αφαιρείται από ένα τροχιακό sp3, ο συντονισμός καλείται μεταξύ τεσσάρων δομών δεσμού σθένους, καθεμία από τις οποίες έχει έναν δεσμό ενός μόνο ηλεκτρονίου και τρεις δύο δεσμούς ηλεκτρονίων. Οι τριπλά εκφυλισμένες T2 και A1 ιονισμένες καταστάσεις του (CH4+) παράγονται από διαφορετικούς γραμμικούς συνδυασμούς αυτών των τεσσάρων δομών. Η διαφορά στην ενέργεια μεταξύ της ιονισμένης και της θεμελιώδους κατάστασης δίνει τις δύο ενέργειες ιονισμού. Όπως στο βενζόλιο, σε ουσίες όπως το β- καροτένιο, η χλωροφύλλη ή η αίμη, ορισμένα ηλεκτρόνια στα τροχιακά π απλώνονται σε μοριακά τροχιακά σε μεγάλες αποστάσεις σε ένα μόριο, με αποτέλεσμα απορρόφηση του φωτός σε χαμηλότερες ενέργειες (το ορατό φάσμα), η οποία ευθύνεται για τα χαρακτηριστικά χρώματα αυτών των ουσιών.[18] Αυτό και άλλα φασματοσκοπικά δεδομένα για μόρια εξηγούνται καλά στη θεωρία μοριακών τροχιακών, με έμφαση στις ηλεκτρονικές καταστάσεις που σχετίζονται με πολυκεντρικά τροχιακά, συμπεριλαμβανομένης της ανάμειξης τροχιακών που βασίζεται στις αρχές της αντιστοίχισης της τροχιακής συμμετρίας.[16] Οι ίδιες αρχές μοριακών τροχιακών εξηγούν επίσης φυσικά ορισμένα ηλεκτρικά φαινόμενα, όπως η υψηλή ηλεκτρική αγωγιμότητα στην επίπεδη διεύθυνση των εξαγωνικών ατομικών φύλλων που υπάρχουν στον γραφίτη. Αυτό προκύπτει από τη συνεχή επικάλυψη ζώνης των μισογεμισμένων τροχιακών p και εξηγεί την ηλεκτρική αγωγιμότητα. Η θεωρία των μοριακών τροχιακών αναγνωρίζει ότι ορισμένα ηλεκτρόνια στα ατομικά φύλλα γραφίτη είναι εντελώς απεντοπισμένα σε αυθαίρετες αποστάσεις και βρίσκονται σε πολύ μεγάλα μοριακά τροχιακά που καλύπτουν ένα ολόκληρο φύλλο γραφίτη, και επομένως μερικά ηλεκτρόνια είναι ελεύθερα να κινούνται και επομένως άγουν τον ηλεκτρισμό στο επίπεδο φύλλου, σαν να κατοικούσαν σε ένα μέταλλο.

Παραπομπές

[Επεξεργασία | επεξεργασία κώδικα]
  1. ↑ Daintith, J. (2004). Oxford Dictionary of Chemistry. New York: Oxford University Press. ISBN 978-0-19-860918-6. 
  2. ↑ Licker, Mark, J. (2004). McGraw-Hill Concise Encyclopedia of Chemistry. New York: McGraw-Hill. ISBN 978-0-07-143953-4. CS1 maint: Πολλαπλές ονομασίες: authors list (link)
  3. ↑ 3,0 3,1 Miessler, Gary L.· Fischer, Paul J.· Tarr, Donald A. (8 Απριλίου 2013). Inorganic Chemistry (στα Αγγλικά). Pearson Education. ISBN 978-0-321-91779-9. 
  4. ↑ Coulson, Charles, A. (1952). Valence. Oxford at the Clarendon Press. 
  5. ↑ 5,0 5,1 Elsevier Publishing Company. Spectroscopy, Molecular Orbitals, and Chemical Bonding. Δελτίο τύπου.
  6. ↑ Hückel, Erich (1934). «Theory of free radicals of organic chemistry». Trans. Faraday Soc. 30: 40–52. doi:10.1039/TF9343000040. 
  7. ↑ Lennard-Jones, J.E. (1929). «The electronic structure of some diatomic molecules». Trans. Faraday Soc. 25: 668–686. doi:10.1039/TF9292500668. Bibcode: 1929FaTr...25..668L. 
  8. ↑ Coulson, C.A. Valence (2nd ed., Oxford University Press 1961), p.103
  9. ↑ Pauling, Linus (1931). «The Nature of the Chemical Bond. II. The One-Electron Bond and the Three-Electron Bond.». J. Am. Chem. Soc. 53 (9): 3225–3237. doi:10.1021/ja01360a004. 
  10. ↑ Hall, George G. (1991). «The Lennard-Jones paper of 1929 and the foundations of Molecular Orbital Theory». Advances in Quantum Chemistry 22: 1–6. doi:10.1016/S0065-3276(08)60361-5. ISBN 978-0-12-034822-0. ISSN 0065-3276. Bibcode: 1991AdQC...22....1H. http://www.quantum-chemistry-history.com/LeJo_Dat/LJ-Hall1.htm. 
  11. ↑ E. Hückel, Zeitschrift für Physik, 70, 204 (1931); 72, 310 (1931); 76, 628 (1932); 83, 632 (1933).
  12. ↑ Hückel Theory for Organic Chemists, C. A. Coulson, B. O'Leary and R. B. Mallion, Academic Press, 1978.
  13. ↑ Coulson, C.A. (1938), «Self-consistent field for molecular hydrogen», Mathematical Proceedings of the Cambridge Philosophical Society 34 (2): 204–212, doi:10.1017/S0305004100020089 
  14. ↑ Hall, G.G. (7 August 1950). «The Molecular Orbital Theory of Chemical Valency. VI. Properties of Equivalent Orbitals». Proc. R. Soc. A 202 (1070): 336–344. doi:10.1098/rspa.1950.0104. Bibcode: 1950RSPSA.202..336H. 
  15. ↑ 15,0 15,1 Jensen, Frank (1999). Introduction to Computational Chemistry. John Wiley and Sons. ISBN 978-0-471-98425-2. 
  16. ↑ 16,0 16,1 16,2 Miessler and Tarr (2013), Inorganic Chemistry, 5th ed, 117-165, 475-534.
  17. ↑ Mulliken, R. S. (October 1955). «Electronic Population Analysis on LCAO–MO Molecular Wave Functions. I». The Journal of Chemical Physics 23 (10): 1833–1840. doi:10.1063/1.1740588. ISSN 0021-9606. Bibcode: 1955JChPh..23.1833M. http://dx.doi.org/10.1063/1.1740588. 
  18. ↑ Griffith, J.S. and L.E. Orgel. "Ligand Field Theory". Q. Rev. Chem. Soc. 1957, 11, 381-383

Εξωτερικοί σύνδεσμοι

[Επεξεργασία | επεξεργασία κώδικα]
Ανακτήθηκε από "https://el.wikipedia.org/w/index.php?title=Θεωρία_των_μοριακών_τροχιακών&oldid=10869450"