Κατασκευή του Ριτς

Κατασκευή του Ριτς: αρχή - τέλος

Η κατασκευή των αξόνων του Ριτς είναι μια βασική μέθοδος της περιγραφικής γεωμετρίας για την εύρεση των αξόνων, του ημιάξονα και του ημιάξονα και των κορυφών μιας έλλειψης, ξεκινώντας από δύο συζευγμένες ημιδιαμέτρους. Εάν το κέντρο και ο ημιάξονας μιας έλλειψης έχουν προσδιοριστεί, η έλλειψη μπορεί να σχεδιαστεί με τη χρήση ελλειψογράφου ή με το χέρι (βλέπε έλλειψη).

Η κατασκευή του Ριτς είναι μια κλασική κατασκευή της ευκλείδειας γεωμετρίας, στην οποία επιτρέπονται ως βοηθήματα μόνο ο διαβήτης και ο χάρακας. Η κατασκευή πήρε το όνομά της από τον εφευρέτη της Νταβίντ Ριτς του Μπρουγκ (1801-1868).

Οι συζυγείς διάμετροι εμφανίζονται πάντα αν ένας κύκλος ή μια έλλειψη προβάλλονται παράλληλα (οι ακτίνες είναι παράλληλες) ως εικόνες ορθογωνίων διαμέτρων ενός κύκλου (βλέπε δεύτερο διάγραμμα) ή ως εικόνες των αξόνων μιας έλλειψης. Μια βασική ιδιότητα δύο συζυγών διαμέτρων $d_{1},\;d_{2}$ είναι: Οι εφαπτόμενες στα σημεία της έλλειψης της μιας διαμέτρου είναι παράλληλες με τη δεύτερη διάμετρο (βλ. δεύτερο διάγραμμα).

Κύβος με κύκλους: στρατιωτική προβολή

Η κατασκευή του Ριτς σε 6 βήματα.Δίνονται: το κέντρο C και δύο συζυγείς ημιδιαμέτρους CP, CQ μιας έλλειψης. Αναζητούνται: οι ημιάξονες και οι κορυφές της έλλειψης.

Δήλωση του προβλήματος και λύση

Η παράλληλη προβολή (λοξή ή ορθογραφική) ενός κύκλου που είναι γενικά μια έλλειψη (η ειδική περίπτωση ενός ευθύγραμμου τμήματος ως εικόνα παραλείπεται). Ένα θεμελιώδες έργο στην παραστατική γεωμετρία είναι να σχεδιάσουμε μια τέτοια εικόνα ενός κύκλου. Το διάγραμμα δείχνει μια αξονομετρική προβολή ενός κύβου με 3 κύκλους σε 3 επιφάνειες του κύβου. Το επίπεδο εικόνας για μια αξονομετρική προβολή είναι οριζόντιο. Αυτό σημαίνει ότι ο κύκλος στην κορυφή εμφανίζεται στο πραγματικό του σχήμα (ως κύκλος). Οι εικόνες των κύκλων στις άλλες δύο όψεις είναι προφανώς ελλείψεις με άγνωστους άξονες. Αλλά αναγνωρίζει κανείς σε κάθε περίπτωση τις εικόνες των δύο ορθογώνιων διαμέτρων των κύκλων. Αυτές οι διάμετροι των ελλείψεων δεν είναι πλέον ορθογώνιες αλλά ως εικόνες ορθογώνιων διαμέτρων του κύκλου είναι συζυγείς (οι εφαπτόμενες στα ακραία σημεία της μιας διαμέτρου είναι παράλληλες με την άλλη διάμετρο !). Αυτή είναι μια τυπική κατάσταση στην περιγραφική γεωμετρία:

• Από μια έλλειψη είναι γνωστό το κέντρο $C$ και δύο σημεία $P,Q$ σε δύο συζυγείς διαμέτρους.
• Ανάθεση: να βρεθούν οι άξονες και οι ημιάξονες της έλλειψης.

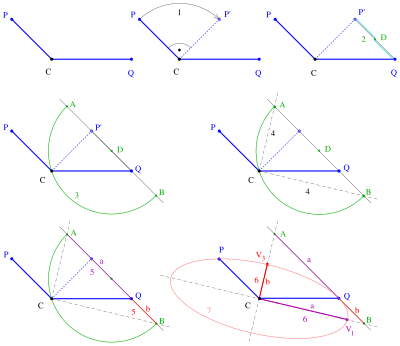
Βήματα της κατασκευής

1. Περιστροφή του σημείου $P$ γύρω από το $C$ κατά 90°.
2. Προσδιορίστε το κέντρο $D$ του ευθύγραμμου τμήματος ${\overline {P'Q}}$.
3. Σχεδιάστε την ευθεία $P'Q$ και τον κύκλο με κέντρο $D$ μέσω του $C$. Να τέμνετε τον κύκλο και την ευθεία. Τα σημεία τομής είναι τα $A,B$.
4. Οι ευθείες $CA$ και $CB$ είναι οι άξονες της έλλειψης
5. Το ευθύγραμμο τμήμα ${\overline {AB}}$ μπορεί να θεωρηθεί ως χαρτοταινία μήκους $a+b$ (βλέπε έλλειψη) που παράγει το σημείο $Q$. Επομένως $a=|AQ|$ και $b=|BQ|$ είναι οι ημι-άξονες. (Αν $a>b$ τότε $a$ είναι ο ημι-μεγάλος άξονας).
6. Οι κορυφές και οι συν-ορθογώνες είναι γνωστές και η έλλειψη μπορεί να σχεδιαστεί με μία από τις μεθόδους σχεδίασης.

Αν γίνει μια αριστερή στροφή του σημείου $P$, τότε η διαμόρφωση δείχνει τη 2η μέθοδο της λωρίδας χαρτιού (βλέπε δεύτερο διάγραμμα στην επόμενη ενότητα) και τα $a=|AQ|$ και $b=|BQ|$ εξακολουθούν να ισχύουν.

Απόδειξη της δήλωσης

Ριτς: απόδειξη

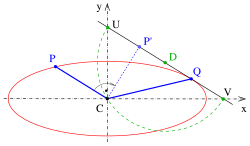
Η τυπική απόδειξη γίνεται γεωμετρικά. Μια εναλλακτική απόδειξη χρησιμοποιεί την αναλυτική γεωμετρία:

Η απόδειξη ολοκληρώνεται, εάν κάποιος είναι σε θέση να δείξει ότι

• τα σημεία τομής $U,V$ της ευθείας $P'Q$ με τους άξονες της έλλειψης βρίσκονται στον κύκλο που διέρχεται από το $C$ με κέντρο $D$, άρα $U=A$ και $V=B$, και $|UQ|=a,\quad |VQ|=b\ .$

Απόδειξη

1. Οποιαδήποτε έλλειψη μπορεί να αναπαρασταθεί σε ένα κατάλληλο σύστημα συντεταγμένων παραμετρικά από

${\vec {p}}(t)=(a\cos t,\;b\sin t)^{T}$.

Δύο σημεία ${\vec {p}}(t_{1}),\ {\vec {p}}(t_{2})$ βρίσκονται σε συζυγείς διαμέτρους αν $t_{2}-t_{1}=\pm {\tfrac {\pi }{2}}\ .$ (βλέπε Έλλειψη: συζυγείς διάμετροι).

2. Έστω $Q=(a\cos t,\;b\sin t)$ και

$P=(a\cos(t+{\tfrac {\pi }{2}}),\;b\sin(t+{\tfrac {\pi }{2}}))=(-a\sin t,b\cos t)$

δύο σημεία σε συζυγείς διαμέτρους.

Τότε $P'=(b\cos t,a\sin t)$ και το μέσο του ευθύγραμμου τμήματος ${\overline {P'Q}}$ είναι $D=\left({\tfrac {a+b}{2}}\cos t,{\tfrac {a+b}{2}}\sin t\right)$.

3. Η γραμμή $P'Q$ έχει εξίσωση $x\sin t+y\cos t=(a+b)\;\cos t\sin t\ .$

Τα σημεία τομής αυτής της ευθείας με τους άξονες της έλλειψης είναι

$U=\left(0,\;(a+b)\sin t\right)\ ,\quad V=\left((a+b)\cos t,\;0\right)\ .$

Rytz: left turn of point $P$

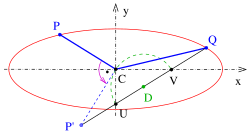
4. Λόγω του $|UD|=|VD|=|CD|$ τα σημεία $U,V,C$ βρίσκονται στον κύκλο με κέντρο $D$ και ακτίνα $|CD|\ .$

Επομένως $A=U,\ B=V\ .$

5. $|UQ|=a,\quad |VQ|=b\ .$

Η απόδειξη χρησιμοποιεί μια δεξιά στροφή του σημείου $P$, η οποία οδηγεί σε ένα διάγραμμα που δείχνει δείχνει τη μέθοδο της 1ης χάρτινης λωρίδας.

Παραλλαγές

Εάν κάποιος πραγματοποιήσει μια αριστερή στροφή του σημείου $P$, τότε τα αποτελέσματα (4) και (5) εξακολουθούν να ισχύουν και η διαμόρφωση δείχνει τώρα τη 2η μέθοδο των χάρτινων λωρίδων (βλέπε διάγραμμα). Αν κάποιος χρησιμοποιήσει $P=(a\cos(t{\color {red}-}{\tfrac {\pi }{2}}),\;b\sin(t{\color {red}-}{\tfrac {\pi }{2}}))=(a\sin t,-b\cos t)$, τότε η κατασκευή και η απόδειξη λειτουργούν είτε.

Λύση με τη βοήθεια υπολογιστή

Να βρείτε τις κορυφές της έλλειψης με τη βοήθεια υπολογιστή,

• πρέπει να είναι γνωστές οι συντεταγμένες των τριών σημείων $C,P,Q$.

Μια απλή ιδέα είναι η εξής: Μπορεί κανείς να γράψει ένα πρόγραμμα που να εκτελεί τα βήματα που περιγράφονται παραπάνω. Μια καλύτερη ιδέα είναι να χρησιμοποιηθεί η αναπαράσταση μιας αυθαίρετης έλλειψης παραμετρικά:

• ${\vec {x}}={\vec {p}}(t)={\vec {f}}_{0}+{\vec {f}}_{1}\cos t+{\vec {f}}_{2}\sin t\ .$

Με ${\vec {f}}_{0}={\vec {OC}}$ (το κέντρο) και ${\vec {f}}_{1}={\vec {CP}},\;{\vec {f}}_{2}={\vec {CQ}}$ (δύο συζυγείς ημιδιαμέτρους) μπορεί κανείς να υπολογίσει τα σημεία και να σχεδιάσει την έλλειψη.

Εάν είναι απαραίτητο: Με $\cot(2t_{0})={\tfrac {{\vec {f}}_{1}^{\,2}-{\vec {f}}_{2}^{\,2}}{2{\vec {f}}_{1}\cdot {\vec {f}}_{2}}}$ παίρνουμε τις τέσσερις κορυφές της έλλειψης: ${\vec {p}}(t_{0}),\;{\vec {p}}(t_{0}\pm {\frac {\pi }{2}}),\;{\vec {p}}(t_{0}+\pi )\ .$

Δημοσιεύσεις

• Scott, J. A. (Νοεμβρίου 2007). «91.68 Bridging parallelograms of equal area». The Mathematical Gazette 91 (522): 530–533. doi:10.1017/S0025557200182257. https://archive.org/details/sim_mathematical-gazette_2007-11_91_522/page/530. 
• Wilhelm Killing: Lehrbuch Der Analytischen Geometrie. Teil 2, Outlook Verlagsgesellschaft, Bremen 2011, ISBN 978-3-86403-540-1.
• Protter, Murray H.; Morrey, Charles B. Jr. (1970), College Calculus with Analytic Geometry (2nd έκδοση), Reading: Addison-Wesley 

• Olivier Faugeras and Q.T. Luong (2001). The Geometry of Multiple Images. MIT Press. ISBN 978-0-262-06220-6. 

• Alican, Necip Fikri (2012). Rethinking Plato: A Cartesian Quest for the Real Plato. Amsterdam and New York: Editions Rodopi B.V. ISBN 978-90-420-3537-9. 
• Allen, R. E. (1965). Studies in Plato's Metaphysics II. Taylor & Francis. ISBN 0-7100-3626-4
• Ambuel, David (2007). Image and Paradigm in Plato's Sophist. Parmenides Publishing. ISBN 978-1-930972-04-9
• Boileau, Michel. «Geometrizations of 3-manifolds with symmetries» (PDF). Αρχειοθετήθηκε από το πρωτότυπο (PDF) στις 30 Σεπτεμβρίου 2011. Ανακτήθηκε στις 6 Δεκεμβρίου 2007. 
• Boileau, Michel· Maillot, Sylvain· Porti, Joan (2003). Three-dimensional orbifolds and their geometric structures. Panoramas and Syntheses. 15. Paris: Société Mathématique de France. ISBN 2-85629-152-X. OCLC 56349823. .
• Boileau, Michel; Leeb, Bernhard; Porti, Joan (2005). «Geometrization of 3-dimensional orbifolds». Annals of Mathematics 162: 195–290. doi:10.4007/annals.2005.162.195. 
• Bredon, Glen (1972). Introduction to Compact Transformation Groups. Academic Press. ISBN 0-12-128850-1. 
• Besant, W.H. (1907). «Chapter III. The Ellipse». Conic Sections. London: George Bell and Sons. σελ. 50. 
• Coxeter, H.S.M. (1969). Introduction to Geometry (2nd έκδοση). New York: Wiley. σελίδες 115–9. 
• Meserve, Bruce E. (1983), Fundamental Concepts of Geometry, Dover Publications, ISBN 978-0-486-63415-9 
• Miller, Charles D.· Lial, Margaret L.· Schneider, David I. (1990). Fundamentals of College Algebra (3rd έκδοση). Scott Foresman/Little. σελ. 381. ISBN 978-0-673-38638-0. 
• Protter, Murray H.; Morrey, Charles B. Jr. (1970), College Calculus with Analytic Geometry (2nd έκδοση), Reading: Addison-Wesley 

Δείτε επίσης

• Field Arithmetic
• Βικιπαίδεια:Εγχειρίδιο μορφής/Μαθηματικά (Περιέχει και τα αγγλοελληνικά Λεξικά Μαθηματικής Ορολογίας)
• Πραγματικό προβολικό επίπεδο
• Στοιχεία του Ευκλείδη
• Ευκλείδειος χώρος
• Καρτεσιανό σύστημα συντεταγμένων
• Ομογενές πολυώνυμο
• Παραμετρικές εξισώσεις
• Παραβολή (γεωμετρία)
• Προβολή (γραμμική άλγεβρα)
• Σπείρα του Αρχιμήδη
• Συνέχεια συνάρτησης
• Διαβήτης (όργανο)
• Ομάδα συμμετρίας
• Ελλειψογράφος του Αρχιμήδη
• Διανυσματικός χώρος
• Έλλειψη (γεωμετρία)
• Μονοδύναμο στοιχείο
• High performance algorithms for reduction to condensed (Hessenberg, tridiagonal, bidiagonal) form

Εξωτερικοί σύνδεσμοι

• Ευκλείδεια Γεωμετρία - Πανελλήνιο Σχολικό Δίκτυο
• Euclid’s elements of geometry - The Greek text of J.L. Heiberg (1883–1885) Πανεπιστήμιο του Τέξας στο Όστιν
• Τα οπτικά του Ευκλείδη Διδακτορική Διατριβή - ΕΑΔΔ
• A History of Greek Mathematics, Τόμος 1
• A History of Greek Mathematics: Τόμος 2
• Advanced Euclidean Geometry
• Methods for Euclidean Geometry.
• Exploring Advanced Euclidean Geometry with GeoGebra.
• Mechanical and Aerospace Engineering, ICMAE2011
• Geometry by Its History
• The VNR Concise Encyclopedia of Mathematics
• Pattern Recognition: 8th Mexican Conference, MCPR 2016, Guanajuato, Mexico .....
• The Universe of Conics: From the ancient Greeks to 21st century developments
• Unipotent and Nilpotent Classes in Simple Algebraic Groups and Lie Algebras..

Παραπομπές

• Rudolf Fucke· Konrad Kirch· Heinz Nickel (2007). Darstellende Geometrie für Ingenieure [Descriptive geometry for engineers] (στα German) (17th έκδοση). München: Carl Hanser. σελ. 183. ISBN 978-3446411432. Ανακτήθηκε στις 31 Μαΐου 2013. 
• Klaus Ulshöfer· Dietrich Tilp (2010). «5: Ellipse als orthogonal-affines Bild des Hauptkreises» [5: "Ellipse as the orthogonal affine image of the unit circle"]. Darstellende Geometrie in systematischen Beispielen [Descriptive geometry in systematic collection of examples]. Übungen für die gymnasiale Oberstufe (στα German) (1st έκδοση). Bamberg: C. C. Buchner. ISBN 978-3-7661-6092-8. 
• Alexander Ostermann· Gerhard Wanner (2012). Geometry by its History. Springer Science & Business Media. σελίδες 68–69. ISBN 9783642291630.