Προσανατολισμός (γεωμετρία)

- Αυτό το άρθρο αναφέρεται στον προσανατολισμό ή τη στάση ενός αντικειμένου ή ενός σχήματος σε έναν χώρο. Για τον προσανατολισμό ενός χώρου, βλ. Δυνατότητα προσανατολισμού (μαθηματικά)
Στη γεωμετρία, ο προσανατολισμός, - όπως μια γραμμή, ένα επίπεδο ή ένα άκαμπτο σώμα -αποτελεί μέρος της περιγραφής του τρόπου με τον οποίο ένα αντικείμενο τοποθετείται στο χώρο που καταλαμβάνει[1]. Πιο συγκεκριμένα, αναφέρεται στη νοητή περιστροφή που απαιτείται για να μετακινηθεί το αντικείμενο από μια θέση αναφοράς στην τρέχουσα θέση του. Μια περιστροφή μπορεί να μην είναι αρκετή για να επιτευχθεί η τρέχουσα τοποθέτηση, οπότε μπορεί να χρειαστεί να προστεθεί μια νοητή μετάθεση για να αλλάξει η θέση (ή η γραμμική θέση) του αντικειμένου. Η θέση και ο προσανατολισμός μαζί περιγράφουν πλήρως τον τρόπο τοποθέτησης του αντικειμένου στο χώρο. Η προαναφερθείσα νοητή περιστροφή και μετάθεση μπορεί να θεωρηθεί ότι συμβαίνουν με οποιαδήποτε σειρά, καθώς ο προσανατολισμός ενός αντικειμένου δεν αλλάζει όταν μεταφράζεται και η θέση του δεν αλλάζει όταν περιστρέφεται.
Το θεώρημα περιστροφής του Όιλερ[2] δείχνει ότι σε τρεις διαστάσεις οποιοσδήποτε προσανατολισμός μπορεί να επιτευχθεί με μία μόνο περιστροφή γύρω από έναν σταθερό άξονα. Αυτό δίνει έναν κοινό τρόπο αναπαράστασης του προσανατολισμού χρησιμοποιώντας μια αναπαράσταση άξονα-γωνίας. Άλλες ευρέως χρησιμοποιούμενες μέθοδοι περιλαμβάνουν τετραγωνικά περιστροφής, περιστροφείς, γωνίες Όιλερ ή πίνακες περιστροφής. Πιο εξειδικευμένες χρήσεις περιλαμβάνουν τους δείκτες Μίλερ στην κρυσταλλογραφία, το strike και dip στη γεωλογία και τη βαθμίδα σε χάρτες και πινακίδες. Ένα μοναδιαίο διάνυσμα μπορεί επίσης να χρησιμοποιηθεί για να αναπαραστήσει την κανονική κατεύθυνση του διανύσματος ενός αντικειμένου ή τη σχετική κατεύθυνση μεταξύ δύο σημείων.
Συνήθως, ο προσανατολισμός δίνεται σε σχέση με ένα σύστημα αναφοράς, το οποίο συνήθως καθορίζεται από ένα καρτεσιανό σύστημα συντεταγμένων.
Μαθηματικές αναπαραστάσεις
[Επεξεργασία | επεξεργασία κώδικα]Τρεις διαστάσεις
[Επεξεργασία | επεξεργασία κώδικα]Κατά κανόνα, η θέση και ο προσανατολισμός στο χώρο ενός άκαμπτου σώματος ορίζονται ως η θέση και ο προσανατολισμός, σε σχέση με το κύριο σύστημα αναφοράς, ενός άλλου συστήματος αναφοράς, το οποίο είναι σταθερό σε σχέση με το σώμα και, ως εκ τούτου, μετατοπίζεται και περιστρέφεται μαζί του (τοπικό σύστημα αναφοράς του σώματος ή τοπικό σύστημα συντεταγμένων). Για την περιγραφή του προσανατολισμού αυτού του τοπικού πλαισίου απαιτούνται τουλάχιστον τρεις ανεξάρτητες τιμές. Τρεις άλλες τιμές περιγράφουν τη θέση ενός σημείου στο αντικείμενο. Όλα τα σημεία του σώματος αλλάζουν τη θέση τους κατά τη διάρκεια μιας περιστροφής εκτός από εκείνα που βρίσκονται πάνω στον άξονα περιστροφής. Εάν το άκαμπτο σώμα έχει περιστροφική συμμετρία, δεν είναι δυνατό να διακριθούν όλοι οι προσανατολισμοί, παρά μόνο παρατηρώντας πώς ο προσανατολισμός εξελίσσεται στο χρόνο από έναν γνωστό αρχικό προσανατολισμό. Παραδείγµατος χάριν, ο προσανατολισµός στο χώρο µιας γραµµής, ενός τµήµατος γραµµής ή ενός διανύσµατος µπορεί να καθοριστεί µε δύο µόνο τιµές, όπως δύο συνηµιτόνια κατεύθυνσης. Ένα άλλο παράδειγμα είναι η θέση ενός σημείου στη Γη, η οποία συχνά περιγράφεται χρησιμοποιώντας τον προσανατολισμό μιας ευθείας που το ενώνει με το κέντρο της Γης, μετρούμενη με τη χρήση των δύο γωνιών του γεωγραφικού μήκους και του γεωγραφικού πλάτους. Ομοίως, ο προσανατολισμός ενός επιπέδου μπορεί επίσης να περιγραφεί με δύο τιμές, για παράδειγμα προσδιορίζοντας τον προσανατολισμό μιας ευθείας κάθετης στο επίπεδο αυτό, ή χρησιμοποιώντας τις γωνίες πρόσπτωσης και βύθισης.
Περισσότερες λεπτομέρειες σχετικά με τις μαθηματικές μεθόδους για την αναπαράσταση του προσανατολισμού άκαμπτων σωμάτων και επιπέδων σε τρεις διαστάσεις δίνονται στις επόμενες ενότητες.
Δύο διαστάσεις
[Επεξεργασία | επεξεργασία κώδικα]Στις δύο διαστάσεις, ο προσανατολισμός οποιουδήποτε αντικειμένου (γραμμή, διάνυσμα ή επίπεδο σχήμα) δίνεται από μία μόνο τιμή: τη γωνία κατά την οποία έχει περιστραφεί. Υπάρχει μόνο ένας βαθμός ελευθερίας και μόνο ένα σταθερό σημείο γύρω από το οποίο πραγματοποιείται η περιστροφή.
Πολλαπλές διαστάσεις
[Επεξεργασία | επεξεργασία κώδικα]Όταν υπάρχουν d διαστάσεις, ο προσδιορισμός του προσανατολισμού ενός αντικειμένου που δεν έχει καμία περιστροφική συμμετρία απαιτεί d(d − 1) / 2 ανεξάρτητες τιμές.
Άκαμπτο σώμα σε τρεις διαστάσεις
[Επεξεργασία | επεξεργασία κώδικα]Διάφορες μέθοδοι για την περιγραφή των προσανατολισμών ενός άκαμπτου σώματος σε τρεις διαστάσεις έχουν αναπτυχθεί. Συνοψίζονται στις ακόλουθες ενότητες.
Γωνίες Όιλερ
[Επεξεργασία | επεξεργασία κώδικα]Κύριο άρθρο: γωνίες Όιλερ Η πρώτη προσπάθεια αναπαράστασης ενός προσανατολισμού αποδίδεται στον Λέοναρντ Όιλερ. Φαντάστηκε τρία πλαίσια αναφοράς που μπορούσαν να περιστρέφονται το ένα γύρω από το άλλο και συνειδητοποίησε ότι ξεκινώντας με ένα σταθερό πλαίσιο αναφοράς και εκτελώντας τρεις περιστροφές, μπορούσε να πάρει οποιοδήποτε άλλο πλαίσιο αναφοράς στο χώρο (χρησιμοποιώντας δύο περιστροφές για να σταθεροποιήσει τον κατακόρυφο άξονα και άλλη μία για να σταθεροποιήσει τους άλλους δύο άξονες). Οι τιμές αυτών των τριών περιστροφών ονομάζονται γωνίες Όιλερ.
Με βάση αυτό το γεγονός εισήγαγε έναν διανυσματικό τρόπο περιγραφής οποιασδήποτε περιστροφής, με ένα διάνυσμα στον άξονα περιστροφής και μονάδα ίση με την τιμή της γωνίας. Επομένως, οποιοσδήποτε προσανατολισμός μπορεί να αναπαρασταθεί από ένα διάνυσμα περιστροφής (που ονομάζεται επίσης διάνυσμα Όιλερ) που οδηγεί σε αυτόν από το σύστημα αναφοράς. Όταν χρησιμοποιείται για την αναπαράσταση ενός προσανατολισμού, το διάνυσμα περιστροφής ονομάζεται συνήθως διάνυσμα προσανατολισμού ή διάνυσμα στάσης.
Γωνίες Τέιτ – Μπράιαν
[Επεξεργασία | επεξεργασία κώδικα]Κύριο άρθρο: γωνίες Όιλερ § Γωνίες Τέιτ–Μπράιαν

Πρόκειται για τρεις γωνίες, επίσης γνωστές ως γωνία εκτροπής, κλίσης και κύλισης, γωνίες πλοήγησης και γωνίες Καρντάν. Μαθηματικά αποτελούν ένα σύνολο έξι δυνατοτήτων μέσα στα δώδεκα πιθανά σύνολα γωνιών Όιλερ, η σειρά είναι αυτή που χρησιμοποιείται καλύτερα για την περιγραφή του προσανατολισμού ενός οχήματος, όπως ένα αεροπλάνο. Στην αεροδιαστημική μηχανική αναφέρονται συνήθως ως γωνίες Όιλερ.

Διάνυσμα προσανατολισμού
[Επεξεργασία | επεξεργασία κώδικα]Ο Όιλερ συνειδητοποίησε επίσης ότι η σύνθεση δύο περιστροφών είναι ισοδύναμη με μια απλή περιστροφή γύρω από διαφορετικό σταθερό άξονα (θεώρημα περιστροφής του Όιλερ). Επομένως, η σύνθεση των τριών προηγούμενων γωνιών πρέπει να ισούται με μία μόνο περιστροφή, ο άξονας της οποίας ήταν περίπλοκο να υπολογιστεί μέχρι να αναπτυχθούν οι πίνακες.
Με βάση αυτό το γεγονός εισήγαγε έναν διανυσματικό τρόπο περιγραφής οποιασδήποτε περιστροφής, με ένα διάνυσμα στον άξονα περιστροφής και μονάδα ίση με την τιμή της γωνίας. Επομένως, οποιοσδήποτε προσανατολισμός μπορεί να αναπαρασταθεί από ένα διάνυσμα περιστροφής (που ονομάζεται επίσης διάνυσμα Όιλερ) που οδηγεί σε αυτόν από το σύστημα αναφοράς. Όταν χρησιμοποιείται για την αναπαράσταση ενός προσανατολισμού, το διάνυσμα περιστροφής ονομάζεται συνήθως διάνυσμα προσανατολισμού ή διάνυσμα στάσης.
Μια παρόμοια μέθοδος, που ονομάζεται αναπαράσταση άξονα-γωνίας, περιγράφει μια περιστροφή ή έναν προσανατολισμό χρησιμοποιώντας ένα μοναδιαίο διάνυσμα ευθυγραμμισμένο με τον άξονα περιστροφής και μια ξεχωριστή τιμή για να υποδείξει τη γωνία (βλ. σχήμα).
Πίνακας προσανατολισμού
[Επεξεργασία | επεξεργασία κώδικα]Κύριο άρθρο: Πίνακας περιστροφής
Με την εισαγωγή των πινάκων, τα θεωρήματα του Όιλερ ξαναγράφτηκαν. Οι περιστροφές περιγράφηκαν από ορθογώνιους πίνακες που αναφέρονται ως πίνακες περιστροφής ή πίνακες συνημίτονου κατεύθυνσης. Όταν χρησιμοποιείται για την αναπαράσταση ενός προσανατολισμού, ένας πίνακας περιστροφής ονομάζεται συνήθως πίνακας προσανατολισμού ή πίνακας στάσης.
Το προαναφερθέν διάνυσμα Όιλερ είναι το ιδιοδιάνυσμα ενός πίνακα περιστροφής (ένας πίνακας περιστροφής έχει μια μοναδική πραγματική ιδιοτιμή). Το γινόμενο δύο πινάκων περιστροφής είναι η σύνθεση των περιστροφών. Επομένως, όπως και προηγουμένως, ο προσανατολισμός μπορεί να δοθεί ως η περιστροφή από το αρχικό πλαίσιο για να επιτευχθεί το πλαίσιο που θέλουμε να περιγράψουμε.
Ο χώρος διαμόρφωσης ενός μη συμμετρικού αντικειμένου στον n-διάστατο χώρο είναι SO(n) × Rn. Ο προσανατολισμός μπορεί να απεικονιστεί με την προσάρτηση μιας βάσης εφαπτόμενων διανυσμάτων σε ένα αντικείμενο. Η κατεύθυνση προς την οποία δείχνει κάθε διάνυσμα καθορίζει τον προσανατολισμό του.
Προσανατολισμός τετραδονίου
[Επεξεργασία | επεξεργασία κώδικα]Ένας άλλος τρόπος για να περιγράψουμε τις περιστροφές είναι η χρήση τετραδόνιο περιστροφής, που ονομάζεται επίσης versors. Είναι ισοδύναμα με τους πίνακες περιστροφής και τα διανύσματα περιστροφής. Όσον αφορά τα διανύσματα περιστροφής, μπορούν να μετατραπούν ευκολότερα σε και από πίνακες. Όταν χρησιμοποιούνται για την αναπαράσταση προσανατολισμών, τα τετραδόνια περιστροφής ονομάζονται συνήθως τετραδόνια προσανατολισμού.
Παραδείγματα χρήσης
[Επεξεργασία | επεξεργασία κώδικα]Στέρεο ή άκαμπτο σώμα
[Επεξεργασία | επεξεργασία κώδικα]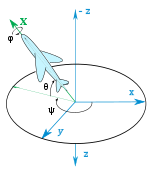
Η στάση ενός άκαμπτου σώματος είναι ο προσανατολισμός του, όπως περιγράφεται, για παράδειγμα, από τον προσανατολισμό ενός πλαισίου που είναι στερεωμένο στο σώμα σε σχέση με ένα σταθερό πλαίσιο αναφοράς. Η στάση περιγράφεται από τις συντεταγμένες στάσης και αποτελείται από τουλάχιστον τρεις συντεταγμένες[3]. Ένα σχήμα για τον προσανατολισμό ενός άκαμπτου σώματος βασίζεται στην περιστροφή των αξόνων του σώματος- διαδοχικές περιστροφές τρεις φορές γύρω από τους άξονες του σταθερού πλαισίου αναφοράς του σώματος, καθορίζοντας έτσι τις γωνίες Όιλερ του σώματος.[4][5]. Ένα άλλο σχήμα βασίζεται στην κύλιση, το βήμα και την κλίση,[6] αν και οι όροι αυτοί αναφέρονται επίσης σε αυξητικές αποκλίσεις από την ονομαστική στάση.
Δημοσιεύσεις
[Επεξεργασία | επεξεργασία κώδικα]- Scott, J. A. (Νοεμβρίου 2007). «91.68 Bridging parallelograms of equal area». The Mathematical Gazette 91 (522): 530–533. doi:. https://archive.org/details/sim_mathematical-gazette_2007-11_91_522/page/530.
- Wilhelm Killing: Lehrbuch Der Analytischen Geometrie. Teil 2, Outlook Verlagsgesellschaft, Bremen 2011, ISBN 978-3-86403-540-1.
- Protter, Murray H.; Morrey, Charles B. Jr. (1970), College Calculus with Analytic Geometry (2nd έκδοση), Reading: Addison-Wesley
- Olivier Faugeras and Q.T. Luong (2001). The Geometry of Multiple Images. MIT Press. ISBN 978-0-262-06220-6.
- Overmars, M. H.; van Leeuwen, J. (1981), «Maintenance of configurations in the plane», Journal of Computer and System Sciences 23 (2): 166–204, doi:.
- Richard Hartley and Andrew Zisserman (2003). Multiple View Geometry in Computer Vision. Cambridge University Press. ISBN 978-0-521-54051-3.
- Günter M. Ziegler's homepage, including a list of editions and translations.
- Shepherd, Mary (2002-08-15). «Review of Proofs from THE BOOK». MAA Reviews (Mathematical Association of America). Αρχειοθετήθηκε από το πρωτότυπο στις 2024-05-27. https://web.archive.org/web/20240527213622/https://maa.org/press/maa-reviews/proofs-from-the-book-1. Ανακτήθηκε στις 2024-10-05.
- Alsina, Claudi; Nelsen, Roger B. (2009), When less is more: Visualizing basic inequalities, The Dolciani Mathematical Expositions, 36, Mathematical Association of America, Washington, DC, ISBN 978-0-88385-342-9
- Barany, Michael (2011), «God, king, and geometry: revisiting the introduction to Cauchy's Cours d'analyse», Historia Mathematica 38 (3): 368–388, doi:
- Boyer, C.: The concepts of the calculus. Hafner Publishing Company, 1949.
- Artin, Emil (1988), Geometric Algebra, Wiley Classics Library, New York: John Wiley & Sons Inc., σελ. x+214, doi:, ISBN 0-471-60839-4
- Ball, W.W. Rouse (1960) [1908]. A Short Account of the History of Mathematics
 (4th έκδοση). Dover Publications. ISBN 0-486-20630-0.
(4th έκδοση). Dover Publications. ISBN 0-486-20630-0.
- Arribas, M.; Elipe, A.; Palacios, M. (2006). «Quaternions and the rotations of a rigid body». Celest. Mech. Dyn. Astron. 96 (3–4): 239–251. doi:. Bibcode: 2006CeMDA..96..239A.
Δείτε επίσης
[Επεξεργασία | επεξεργασία κώδικα]- Field Arithmetic
- Βικιπαίδεια:Εγχειρίδιο μορφής/Μαθηματικά (Περιέχει και τα αγγλοελληνικά Λεξικά Μαθηματικής Ορολογίας)
- Πραγματικό προβολικό επίπεδο
- Στοιχεία του Ευκλείδη
- Ευκλείδειος χώρος
- Καρτεσιανό σύστημα συντεταγμένων
- Ομογενές πολυώνυμο
- Παραμετρικές εξισώσεις
- Παραβολή (γεωμετρία)
- Προβολή (γραμμική άλγεβρα)
- Σπείρα του Αρχιμήδη
- Συνέχεια συνάρτησης
- Διπλή εφαπτομένη
- Γεωγραφικό πλάτος
- Κυρτό πολύτοπο
- Τετραγωνισμός του κύκλου
- Γεωγραφικό μήκος
- Μονοδύναμο στοιχείο
- High performance algorithms for reduction to condensed (Hessenberg, tridiagonal, bidiagonal) form
Εξωτερικοί σύνδεσμοι
[Επεξεργασία | επεξεργασία κώδικα]- Ευκλείδεια Γεωμετρία - Πανελλήνιο Σχολικό Δίκτυο
- Euclid’s elements of geometry - The Greek text of J.L. Heiberg (1883–1885) Πανεπιστήμιο του Τέξας στο Όστιν
- A History of Greek Mathematics, Τόμος 1
- A History of Greek Mathematics: Τόμος 2
- Advanced Euclidean Geometry
- Methods for Euclidean Geometry.
- Exploring Advanced Euclidean Geometry with GeoGebra.
- Methods for Euclidean Geometry
- Oriented Projective Geometry: A Framework for Geometric Computations
- Handbook of Differential Geometry
- Orientations and Rotations: Computations in Crystallographic Textures
- Exploring Classical Greek Construction Problems with Interactive Geometry ....
- Unipotent and Nilpotent Classes in Simple Algebraic Groups and Lie Algebras..
Παραπομπές
[Επεξεργασία | επεξεργασία κώδικα]- ↑
Robert J. Twiss· Eldridge M. Moores (1992). «§2.1 The orientation of structures». Structural Geology (2nd έκδοση). Macmillan. σελ. 11. ISBN 0-7167-2252-6.
...the attitude of a plane or a line — that is, its orientation in space — is fundamental to the description of structures.
- ↑ Palais, Bob; Palais, Richard; Rodi, Stephen (2009-12-01). «A Disorienting Look at Euler's Theorem on the Axis of a Rotation» (στα αγγλικά). American Mathematical Monthly 116 (10): 892–909. doi:. https://www.tandfonline.com/doi/full/10.4169/000298909X477014.
- ↑ Hanspeter Schaub· John L. Junkins (2003). «Rigid body kinematics». Analytical Mechanics of Space Systems. American Institute of Aeronautics and Astronautics. σελ. 71. ISBN 1-56347-563-4.
- ↑ Jack B. Kuipers (2002). «Figure 4.7: Aircraft Euler angle sequence». Quaternions and Rotation Sequences: A Primer with Applications to Orbits, Aerospace, and Virtual Reality. Princeton University Press. σελ. 85. ISBN 0-691-10298-8.
- ↑
Bong Wie (1998). «§5.2 Euler angles». Space Vehicle Dynamics and Control
 . American Institute of Aeronautics and Astronautics. σελ. 310. ISBN 1-56347-261-9.
. American Institute of Aeronautics and Astronautics. σελ. 310. ISBN 1-56347-261-9. Euler angle rigid body attitude.
- ↑ Lorenzo Sciavicco· Bruno Siciliano (2000). «§2.4.2 Roll–pitch–yaw angles». Modelling and Control of Robot Manipulators (2nd έκδοση). Springer. σελ. 32. ISBN 1-85233-221-2.
- A. L. Cauchy, "Recherche sur les polyèdres – premier mémoire", Journal de l'École Polytechnique 9 (1813), 66–86.
- An interactive tutorial on Euler angles available at https://www.mecademic.com/en/how-is-orientation-in-space-represented-with-euler-angles
- EulerAngles – an iOS app for visualizing in 3D the three rotations associated with Euler angles
- Orientation Library – "orilib", a collection of routines for rotation / orientation manipulation, including special tools for crystal orientations
- Online tool to convert rotation matrices available at rotation converter (numerical conversion)
