Σπειροειδής ομοιότητα

Μια σπειροειδής ομοιότητα που μεταφέρει το τρίγωνο ABC στο τρίγωνο A'B'C'.

Η σπειροειδής ομοιότητα είναι ένας μετασχηματισμός επιπέδου στα μαθηματικά που αποτελείται από μια περιστροφή και μια διαστολή. Χρησιμοποιείται ευρέως στην Ευκλείδεια γεωμετρία για να διευκολύνει την απόδειξη πολλών θεωρημάτων και άλλων αποτελεσμάτων στη γεωμετρία, ιδίως σε μαθηματικούς διαγωνισμούς και ολυμπιάδες. Αν και η προέλευση αυτής της ιδέας δεν είναι γνωστή, καταγράφηκε το 1967 από τον Κόξετερ στο βιβλίο του Geometry Revisited (Αναθεώρηση της γεωμετρίας) και το 1969 - χρησιμοποιώντας τον όρο «dilative rotation» - στο βιβλίο του Introduction to Geometry (Εισαγωγή στη Γεωμετρία).

Το ακόλουθο θεώρημα είναι σημαντικό για το ευκλείδειο επίπεδο:
Κάθε δύο άμεσα όμοια σχήματα συνδέονται είτε με μετατόπιση είτε με σπειροειδή ομοιότητα.
(Συμβουλή: Τα άμεσα όμοια σχήματα είναι όμοια και έχουν τον ίδιο προσανατολισμό)

Ορισμός

Μια σπειροειδής ομοιότητα $S$ αποτελείται από μια περιστροφή του επιπέδου που ακολουθείται από μια διαστολή γύρω από ένα κέντρο $O$ με συντεταγμένες $c$ στο επίπεδο. Εκφράζοντας την περιστροφή με έναν γραμμικό μετασχηματισμό $T(x)$ και τη διαστολή ως πολλαπλασιασμό με έναν παράγοντα κλίμακας $d$, ένα σημείο $p$ αντιστοιχίζεται σε

$S(p)=d(T(p-c))+c.$

Στο μιγαδικό επίπεδο, οποιαδήποτε σπειροειδής ομοιότητα μπορεί να εκφραστεί με τη μορφή $T(x)=x_{0}+\alpha (x-x_{0})$, όπου $\alpha$ είναι ένας μιγαδικός αριθμός. Το μέγεθος $|\alpha |$ είναι ο παράγοντας διαστολής της σπειροειδούς ομοιότητας και το επιχείρημα ${\text{arg}}(\alpha )$ είναι η γωνία περιστροφής.

Ιδιότητες

Δύο κύκλοι

Σπειροειδής ομοιότητα

Έστω T μια σπειροειδής ομοιότητα που απεικονίζει τον κύκλο k στον k' με k $\cap$ k' = {C, D} και σταθερό σημείο C.

Τότε για κάθε σημείο P $\in$ k τα σημεία P, T(P)= P' και D είναι συγγραμμικά.

Παρατήρηση: Αυτή η ιδιότητα είναι η βάση για την κατασκευή του κέντρου μιας σπειροειδούς ομοιότητας για δύο γραμμικά τμήματα.

Απόδειξη:

$\angle CMP=\angle CM'P'$, καθώς η περιστροφή και η διαστολή διατηρούν τις γωνίες.

$\angle P'DC+\angle CDP=180^{\circ }$, καθώς αν η ακτίνα ${\overline {MD}}$ τέμνει τη χορδή ${\overline {CP}}$ , τότε η ${\overline {M'D}}$ δεν συναντά την ${\overline {CP'}}$ , και αν η ${\overline {MD}}$ δεν τέμνει την ${\overline {CP}}$, τότε η ${\overline {M'D}}$ τέμνει την ${\overline {CP'}}$, οπότε η μία από αυτές τις γωνίες είναι $\beta$ και η άλλη είναι $180^{\circ }-\beta$.

Επομένως, τα P, P' και D είναι συγγραμμικά.

Κέντρο σπειροειδούς ομοιότητας για δύο ευθύγραμμα τμήματα

Μέσω της διαστολής μιας γραμμής, της περιστροφής και της μεταφοράς, οποιοδήποτε ευθύγραμμο τμήμα μπορεί να απεικονιστεί σε οποιοδήποτε άλλο μέσω της σειράς των μετασχηματισμών του επιπέδου. Μπορούμε να βρούμε το κέντρο της σπειροειδούς ομοιότητας μέσω της ακόλουθης κατασκευής:

• Σχεδιάστε τις ευθείες ${\overline {AC}}$ και ${\overline {BD}}$, και έστω $P$ η τομή των δύο ευθειών.
• Σχεδιάστε τις περιμέτρους των τριγώνων $\triangle PAB$ and $\triangle PCD$.
• Οι περίκυκλοι τέμνονται σε ένα δεύτερο σημείο $X\neq P$. Τότε το $X$ είναι το κέντρο της σπείρας που απεικονίζει την ${\overline {AB}}$ στην ${\overline {CD}}.$

Απόδειξη: Σημειώστε ότι τα $ABPX$ και $XPCD$ είναι εγγεγραμμένα τετράπλευρα. Επομένως, $\angle XAB=180^{\circ }-\angle BPX=\angle XPD=\angle XCD$. Ομοίως, $\angle ABX=\angle APX=180^{\circ }-\angle XPC=\angle XDC$. Συνεπώς, από την ομοιότητα ΑΑ, τα τρίγωνα $XAB$ και $XCD$ είναι όμοια. Επομένως, $\angle AXB=\angle CXD,$ οπότε μια γωνία περιστροφής που απεικονίζει το $A$ στο $B$ απεικονίζει επίσης το $C$ στο $D$. Ο συντελεστής διαστολής είναι τότε απλώς ο λόγος των μηκών των πλευρών ${\overline {CD}}$ προς ${\overline {AB}}$.

Λύση με μιγαδικούς αριθμούς

Αν εκφράσουμε τα $A,B,C,$ και $D$ ως σημεία στο μιγαδικό επίπεδο με αντίστοιχους μιγαδικούς αριθμούς $a,b,c,$ και $d$, μπορούμε να λύσουμε την έκφραση της σπειροειδούς ομοιότητας που οδηγεί το $A$ στο $C$ και το $B$ στο $D$. Σημειώστε ότι $T(a)=x_{0}+\alpha (a-x_{0})$ και $T(b)=x_{0}+\alpha (b-x_{0})$, οπότε ${\frac {T(b)-T(a)}{b-a}}=\alpha$. Δεδομένου ότι $T(a)=c$ και $T(b)=d$, συνδέουμε για να λάβουμε $\alpha ={\frac {d-c}{b-a}}$, από το οποίο προκύπτει $x_{0}={\frac {ad-bc}{a+d-b-c}}$.

Ζεύγη σπειροειδών ομοιοτήτων

Για οποιαδήποτε σημεία $A,B,C,$ και $D$, το κέντρο της σπειροειδούς ομοιότητας που παίρνει ${\overline {AB}}$ προς ${\overline {CD}}$ είναι επίσης το κέντρο μιας σπειροειδούς ομοιότητας που παίρνει ${\overline {AC}}$ προς ${\overline {BD}}$.

Αυτό μπορεί να γίνει αντιληπτό μέσω της παραπάνω κατασκευής. Αν αφήσουμε $X$ να είναι το κέντρο της σπειροειδούς ομοιότητας που παίρνει την ${\overline {AB}}$ με την ${\overline {CD}}$, τότε $\triangle XAB\sim \triangle XCD$. Επομένως, $\angle AXC=\angle AXB+\angle BXC=\angle CXD+\angle BXC=\angle BXD$. Επίσης, ${\frac {AX}{BX}}={\frac {CX}{DX}}$ συνεπάγεται ότι ${\frac {AX}{CX}}={\frac {BX}{DX}}$. Έτσι, μέσω της ομοιότητας SAS, βλέπουμε ότι $\triangle AXC\sim \triangle BXD$. Έτσι, το $X$ είναι επίσης το κέντρο της σπειροειδούς ομοιότητας που οδηγεί την ${\overline {AC}}$ στην ${\overline {BD}}$.

Συμπεράσματα

Απόδειξη του τετραπλευρικού θεωρήματος του Μικέλ

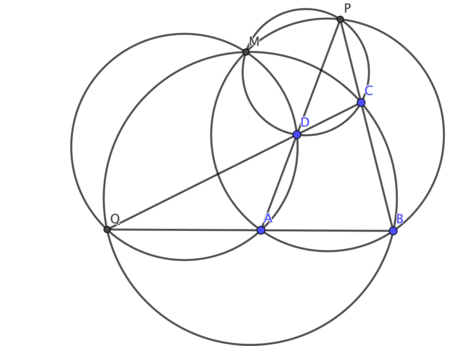
Η σπειροειδής ομοιότητα μπορεί να χρησιμοποιηθεί για την απόδειξη του τετραπλευρικού θεωρήματος του Μικέλ: δεδομένων τεσσάρων μη συγγραμμικών σημείων $A,B,C,$ και $D$, οι περίμετροι των τεσσάρων τριγώνων $\triangle PAB,\triangle PDC,\triangle QAD,$ και $\triangle QBC$ τέμνονται σε ένα σημείο, όπου $P$ είναι η τομή των $AD$ και $BC$ και $Q$ είναι η τομή των $AB$ και $CD$ (βλέπε διάγραμμα).

Έστω $M$ το κέντρο της σπειροειδούς ομοιότητας που οδηγεί το $AB$ στο $DC$. Σύμφωνα με την παραπάνω κατασκευή, οι περίμετροι του $\triangle PAB$ και του $\triangle PDC$ τέμνονται στα $M$ και $P$. Αφού το $M$ είναι επίσης το κέντρο της σπειροειδούς ομοιότητας που παίρνει το $DA$ στο $BC$, με παρόμοιο συλλογισμό οι περίμετροι του $\triangle QAD$ και του $\triangle QBC$ συναντώνται στα $Q$ και $M$. Συνεπώς, και οι τέσσερις κύκλοι τέμνονται στο $M$.

Παράδειγμα προβλήματος

Ακολουθεί ένα πρόβλημα-παράδειγμα για τους τελικούς της Ιαπωνίας 2018 MO, το οποίο μπορεί να λυθεί με τη χρήση της σπειροειδούς ομοιότητας:

Δεδομένου ενός σκαληνού τριγώνου $ABC$, έστω $D$ και $E$ σημεία στα τμήματα $AB$ και $AC$, αντίστοιχα, έτσι ώστε $CA=CD,BA=BE$. Έστω $\omega$ το περίγραμμα του τριγώνου $ADE$ και $P$ η αντανάκλαση του $A$ στο $BC$. Οι ευθείες $PD$ και $PE$ συναντούν το $\omega$ και πάλι στις $X$ και $Y$, αντίστοιχα. Αποδείξτε ότι οι $BX$ και $CY$ τέμνονται στο $\omega$.

Απόδειξη: Αποδεικνύουμε πρώτα τους ακόλουθους ισχυρισμούς:

Ισχυρισμός 1: Το τετράπλευρο $PBEC$ είναι κυκλικό.

Απόδειξη: Αφού το $\triangle BAE$ είναι ισοσκελές, παρατηρούμε ότι $\angle BPC=\angle BAC=180^{\circ }-\angle BEC,$ αποδεικνύοντας έτσι ότι το τετράπλευρο $PBEC$ είναι κυκλικό, όπως είναι επιθυμητό. Με συμμετρία, μπορούμε να αποδείξουμε ότι το τετράπλευρο $PBDC$ είναι κυκλικό.

Ισχυρισμός 2: $\triangle AXY\sim \triangle ABC.$

Απόδειξη: Έχουμε ότι $\angle AXY=180^{\circ }-\angle AEY=\angle YEC=\angle PEC=\angle PBC=\angle ABC.$ Με παρόμοιο συλλογισμό, $\angle AYX=\angle ACB,$ οπότε από την ομοιότητα AA, $\triangle AXY\sim \triangle ABC,$ όπως είναι επιθυμητό.

Σημειώνουμε τώρα ότι το $A$ είναι το σπειροειδές κέντρο που απεικονίζει το $XY$ στο $BC$. Έστω $F$ η τομή των $BX$ και $CY$. Από την παραπάνω κατασκευή της σπειροειδούς ομοιότητας, το κέντρο της σπείρας πρέπει να είναι το σημείο τομής των περιφερειών του $\triangle FXY$ και του $\triangle FBC$. Ωστόσο, το σημείο αυτό είναι το $A$, οπότε τα σημεία $A,F,X,Y$ πρέπει να είναι κυκλικά. Επομένως, το $F$ πρέπει να βρίσκεται στο $\omega$, όπως είναι επιθυμητό.

Δημοσιεύσεις

• Bell, John L. (1999). The Art of the Intelligible: An Elementary Survey of Mathematics in its Conceptual Development. Kluwer. ISBN 0-7923-5972-0. 
• Euclid (1956). The Thirteen Books of Euclid's Elements, Translated from the Text of Heiberg, with Introduction and Commentary. 1 (Books I and II). Μτφρ. Heath, Thomas L. (Reprint of 2nd (1925) έκδοση). Dover.  On-line text at archive.org

• Axler, Sheldon (2015). Linear Algebra Done Right. Undergraduate Texts in Mathematics. Springer. doi:10.1007/978-3-319-11080-6. ISBN 978-3-319-11079-0. Αρχειοθετήθηκε από το πρωτότυπο στις 27 Μαΐου 2022. Ανακτήθηκε στις 17 Απριλίου 2022. 
• Johnson, Roger A. (1929), «X. Inscribed and Escribed Circles», Modern Geometry, Houghton Mifflin, σελ. 182–194, https://archive.org/details/moderngeometry0000unse_q5z5/page/182/ 

• Edwards, Robert D. (1984), «The solution of the 4-dimensional annulus conjecture (after Frank Quinn)», Four-manifold theory (Durham, N.H., 1982), Contemp. Math., 35, Providence, R.I.: Amer. Math. Soc., σελ. 211–264, doi:10.1090/conm/035/780581, ISBN 9780821850336 
• Zazkis, R., Liljedahl, P., & Gadowsky, K. Conceptions of function translation: obstacles, intuitions, and rerouting. Journal of Mathematical Behavior, 22, 437-450. Retrieved April 29, 2014, from www.elsevier.com/locate/jmathb
• Transformations of Graphs: Horizontal Translations. (2006, January 1). BioMath: Transformation of Graphs. Retrieved April 29, 2014
• Farkas, Hershel M.; Kra, Irwin (1980), Riemann Surfaces (2nd έκδοση), Berlin, New York: Springer-Verlag|, ISBN 978-0-387-90465-8 
• Hartshorne, Robin (1977), Algebraic Geometry, Berlin, New York: Springer-Verlag|, ISBN 978-0-387-90244-9, OCLC 13348052 , esp. chapter IV.
• Argand (1814). «Reflexions sur la nouvelle théorie des imaginaires, suives d'une application à la demonstration d'un theorème d'analise» (στα γαλλικά). Annales de mathématiques pures et appliquées 5: 197–209. https://babel.hathitrust.org/cgi/pt?id=uc1.$c126479&view=1up&seq=209. 
• Bourbaki, Nicolas (1998). «Foundations of mathematics § logic: set theory». Elements of the history of mathematics. Springer. 
• Burton, David M. (1995). The History of Mathematics (3rd έκδοση). New York: McGraw-Hill. ISBN 978-0-07-009465-9. 

Δείτε επίσης

• Field Arithmetic
• Βικιπαίδεια:Εγχειρίδιο μορφής/Μαθηματικά (Περιέχει και τα αγγλοελληνικά Λεξικά Μαθηματικής Ορολογίας)
• Πραγματικό προβολικό επίπεδο
• Στοιχεία του Ευκλείδη
• Ευκλείδειος χώρος
• Καρτεσιανό σύστημα συντεταγμένων
• Μιγαδικός αριθμός
• τοπολογικος ισομορφισμός
• Παραβολή (γεωμετρία)
• Προβολή (γραμμική άλγεβρα)
• Πυθαγόρειο θεώρημα
• Διανυσματική προβολή
• Διαβήτης (όργανο)
• Ορθόκεντρο τριγώνου
• Εγγεγραμμένο τετράπλευρο
• Εγγεγραμμένος και Παρεγγεγραμμένοι κύκλοι τριγώνου
• Μιγαδική ανάλυση
• Μιγαδικό επίπεδο
• Διανυσματική προβολή
• High performance algorithms for reduction to condensed (Hessenberg, tridiagonal, bidiagonal) form

Εξωτερικοί σύνδεσμοι

• Ευκλείδεια Γεωμετρία - Πανελλήνιο Σχολικό Δίκτυο
• Euclid’s elements of geometry - The Greek text of J.L. Heiberg (1883–1885) Πανεπιστήμιο του Τέξας στο Όστιν
• Τα οπτικά του Ευκλείδη Διδακτορική Διατριβή - ΕΑΔΔ
• A History of Greek Mathematics, Τόμος 1
• A History of Greek Mathematics: Τόμος 2
• Advanced Euclidean Geometry
• Methods for Euclidean Geometry.
• CRC Concise Encyclopedia of Mathematics page 2802.
• Geometry Turned On: Dynamic Software in Learning, Teaching, and Research.., page 118
• Euclidean Geometry in Mathematical Olympiads, page 198
• USA and International Mathematical Olympiads, 2003 ... page 68...
• Proofs in Competition Math: Volume 1.., page 289
• Geometry Revisited, Τόμος 19, page 98....
• Unipotent and Nilpotent Classes in Simple Algebraic Groups and Lie Algebras..

Παραπομπές

• Anton, Howard; Bivens, Irl C.; Davis, Stephen (2016), Calculus: Early Transcendentals (11th έκδοση), John Wiley & Sons, ISBN 978-1-118-88382-2 
• Apostol, Tom M. (1967), Calculus, Vol. 1: One-Variable Calculus with an Introduction to Linear Algebra (2nd έκδοση), Wiley, ISBN 978-0-471-00005-1, https://archive.org/details/calculus01apos 
• Bourbaki, Nicolas (2004), Integration I, Springer-Verlag, ISBN 3-540-41129-1 . In particular chapters III and IV.
• Flanigan, Francis J. (1983). Complex Variables: Harmonic and Analytic Functions. Dover. ISBN 0-486-61388-7.