Τετραγωνικό πλέγμα

Τετραγωνικά πλέγματα

Όρθιο τετραγωνικό Απλό	διαγώνιο τετραγωνικό κεντραρισμένο

Όρθια τετραγωνική πλακόστρωση. Οι κορυφές όλων των τετραγώνων μαζί με τα κέντρα τους σχηματίζουν ένα όρθιο τετραγωνικό πλέγμα. Για κάθε χρώμα τα κέντρα των τετραγώνων αυτού του χρώματος σχηματίζουν ένα διαγώνιο τετραγωνικό πλέγμα το οποίο είναι σε γραμμική κλίμακα √2 φορές μεγαλύτερο από το όρθιο τετραγωνικό πλέγμα..

Στα μαθηματικά, το τετραγωνικό πλέγμα είναι ένας τύπος πλέγματος σε δισδιάστατο ευκλείδειο χώρο. Είναι η δισδιάστατη εκδοχή του ακέραιου πλέγματος, που συμβολίζεται ως $\mathbb {Z} ^{2}$. Είναι ένας από τους πέντε τύπους δισδιάστατων πλεγμάτων, όπως ταξινομούνται με βάση τις ομάδες συμμετρίας τους, η ομάδα συμμετρίας του σε συμβολισμό IUC ως p4m, σε συμβολισμό Κόξετερ ως [4,4], και σε συμβολισμό orbifold (τροχιακή πολλαπλότητα) ως *442..

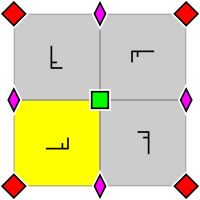
Οι δύο προσανατολισμοί μιας εικόνας του πλέγματος είναι μακράν οι πιο συνηθισμένοι. Μπορούν εύκολα να αναφερθούν ως το όρθιο τετραγωνικό πλέγμα και το διαγώνιο τετραγωνικό πλέγμα- το τελευταίο ονομάζεται επίσης κεντραρισμένο τετραγωνικό πλέγμα . Αυτό σχετίζεται με το γεγονός ότι ένα τετραγωνικό πλέγμα μπορεί να διαιρεθεί σε δύο τετραγωνικά υποπλέγματα, όπως είναι εμφανές στον χρωματισμό μιας σκακιέρας.

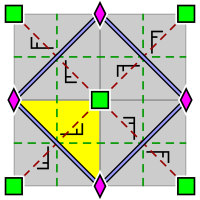
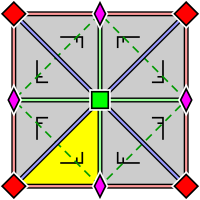
Συμμετρία

Η κατηγορία συμμετρία του τετραγωνικού πλέγματος είναι η ομάδα ταπετσαρίας p4m. Ένα μοτίβο με αυτό το πλέγμα μεταφορικής συμμετρίας δεν μπορεί να έχει περισσότερη, αλλά μπορεί να έχει λιγότερη συμμετρία από το ίδιο το πλέγμα. Ένα όρθιο τετραγωνικό πλέγμα μπορεί να θεωρηθεί ως ένα διαγώνιο τετραγωνικό πλέγμα με μέγεθος ματιού √2 φορές μεγαλύτερο, με τα κέντρα των τετραγώνων να προστίθενται. Αντίστοιχα, μετά την προσθήκη των κέντρων των τετραγώνων ενός όρθιου τετραγωνικού πλέγματος προκύπτει ένα διαγώνιο τετραγωνικό πλέγμα με μέγεθος ματιού √2 φορές μικρότερο από αυτό του αρχικού πλέγματος. Ένα μοτίβο με 4-fold περιστροφική συμμετρία έχει ένα τετραγωνικό πλέγμα 4-fold περιστροφικών κέντρων το οποίο είναι √2 φορές λεπτότερο και διαγώνια προσανατολισμένο σε σχέση με το πλέγμα μεταφορικής συμμετρίας.

Όσον αφορά τους άξονες αντανάκλασης υπάρχουν τρεις δυνατότητες:

• Καμία. Αυτή είναι η ομάδα ταπετσαρίας p4.
• Σε τέσσερις κατευθύνσεις. Αυτή είναι η ομάδα ταπετσαρίας p4m.
• Σε δύο κάθετες κατευθύνσεις. Αυτή είναι η ομάδα ταπετσαριών p4g. Τα σημεία τομής των αξόνων ανάκλασης σχηματίζουν ένα τετραγωνικό πλέγμα το οποίο είναι τόσο λεπτό όσο και προσανατολισμένο όπως το τετραγωνικό πλέγμα των τετραπλών κέντρων περιστροφής (rotocenter), με τα κέντρα περιστροφής αυτά στα κέντρα των τετραγώνων που σχηματίζονται από τους άξονες ανάκλασης.

p4, [4,4]+, (442)	p4g, [4,4+], (4*2)	p4m, [4,4], (*442)
Ομάδα ταπετσαρίας p4, με τη διάταξη μέσα σε ένα πρωτόγονο κύτταρο των 2- και 4-fold περιστροφικών κέντρων (ισχύει επίσης για τις p4g και p4m).   Θεμελιώδης τομέας	Ομάδα ταπετσαρίας p4g. Υπάρχουν άξονες ανάκλασης προς δύο κατευθύνσεις, όχι μέσω των 4fold περιστροφικών κέντρων.   Θεμελιώδης τομέας	Ομάδα ταπετσαριών p4m. Υπάρχουν άξονες ανάκλασης προς τέσσερις κατευθύνσεις, μέσω των 4fold περιστροφικών κέντρων. Σε δύο κατευθύνσεις οι άξονες ανάκλασης έχουν τον ίδιο προσανατολισμό και την ίδια πυκνότητα με αυτούς της p4g, αλλά μετατοπισμένους. Στις άλλες δύο κατευθύνσεις είναι γραμμικά κατά ένα παράγοντα √2 πυκνότεροι.   Θεμελιώδης τομέας

Δημοσιεύσεις

• Scott, J. A. (Νοεμβρίου 2007). «91.68 Bridging parallelograms of equal area». The Mathematical Gazette 91 (522): 530–533. doi:10.1017/S0025557200182257. https://archive.org/details/sim_mathematical-gazette_2007-11_91_522/page/530. 
• Wilhelm Killing: Lehrbuch Der Analytischen Geometrie. Teil 2, Outlook Verlagsgesellschaft, Bremen 2011, ISBN 978-3-86403-540-1.
• Protter, Murray H.; Morrey, Charles B. Jr. (1970), College Calculus with Analytic Geometry (2nd έκδοση), Reading: Addison-Wesley 

• Olivier Faugeras and Q.T. Luong (2001). The Geometry of Multiple Images. MIT Press. ISBN 978-0-262-06220-6. 

• Alican, Necip Fikri (2012). Rethinking Plato: A Cartesian Quest for the Real Plato. Amsterdam and New York: Editions Rodopi B.V. ISBN 978-90-420-3537-9. 
• Allen, R. E. (1965). Studies in Plato's Metaphysics II. Taylor & Francis. ISBN 0-7100-3626-4
• Ambuel, David (2007). Image and Paradigm in Plato's Sophist. Parmenides Publishing. ISBN 978-1-930972-04-9
• Boileau, Michel. «Geometrizations of 3-manifolds with symmetries» (PDF). Αρχειοθετήθηκε από το πρωτότυπο (PDF) στις 30 Σεπτεμβρίου 2011. Ανακτήθηκε στις 6 Δεκεμβρίου 2007. 
• Boileau, Michel· Maillot, Sylvain· Porti, Joan (2003). Three-dimensional orbifolds and their geometric structures. Panoramas and Syntheses. 15. Paris: Société Mathématique de France. ISBN 2-85629-152-X. OCLC 56349823. .
• Boileau, Michel; Leeb, Bernhard; Porti, Joan (2005). «Geometrization of 3-dimensional orbifolds». Annals of Mathematics 162: 195–290. doi:10.4007/annals.2005.162.195. 
• Bredon, Glen (1972). Introduction to Compact Transformation Groups. Academic Press. ISBN 0-12-128850-1. 
• Noam Elkies: Lattices, linear codes, and invariants. Part I (PDF; 156 kB) Notices AMS 47 (2000), No. 10, S. 1238–1245 Part II (PDF; 176 kB) Notices AMS 47 (2000), No. 11, S. 1382–1391
• Hendrik Lenstra: Flags and lattice basis reduction. in Carles Casacuberta et al. (Hrsg.): European Congress of Mathematics. Barcelona 2000, Vol. I. Birkhäuser 2002, ISBN 978-3-7643-6417-5, S. 37–52. Online hier (PDF; 165 kB)
• Oded Regev: Lattices in Computer Science. Tel-Aviv University, 2004
• Daniele Micciancio: Lecture Notes on lattice algorithms and applications University of California, 2007
• Norman Johnson Uniform Polytopes, Manuscript (1991)
• N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
• Norman W. Johnson and Asia Ivic Weiss Quadratic Integers and Coxeter Groups Αρχειοθετήθηκε 2023-03-26 στο Wayback Machine. PDF Can. J. Math. Vol. 51 (6), 1999 pp. 1307–1336
• N. W. Johnson: Geometries and Transformations, (2018) ISBN 978-1-107-10340-5 [1] PDF
• Conway, John Horton; Delgado Friedrichs, Olaf; Huson, Daniel H.; Thurston, William P. (2001), «On three-dimensional space groups», Beiträge zur Algebra und Geometrie 42 (2): 475–507, ISSN 0138-4821, http://www.emis.de/journals/BAG/vol.42/no.2/17.html 

Δείτε επίσης

• Field Arithmetic
• Βικιπαίδεια:Εγχειρίδιο μορφής/Μαθηματικά (Περιέχει και τα αγγλοελληνικά Λεξικά Μαθηματικής Ορολογίας)
• Πραγματικό προβολικό επίπεδο
• Στοιχεία του Ευκλείδη
• Ευκλείδειος χώρος
• Καρτεσιανό σύστημα συντεταγμένων
• Ομογενές πολυώνυμο
• Παραμετρικές εξισώσεις
• Παραβολή (γεωμετρία)
• Προβολή (γραμμική άλγεβρα)
• Σπείρα του Αρχιμήδη
• Συνέχεια συνάρτησης
• Ομάδα Κόξετερ
• Ομάδα συμμετρίας
• Φιλίππο Μπρουνελλέσκι
• Διανυσματικός χώρος
• Γεωγραφικό μήκος
• Μονοδύναμο στοιχείο
• High performance algorithms for reduction to condensed (Hessenberg, tridiagonal, bidiagonal) form

Εξωτερικοί σύνδεσμοι

• Ευκλείδεια Γεωμετρία - Πανελλήνιο Σχολικό Δίκτυο
• Euclid’s elements of geometry - The Greek text of J.L. Heiberg (1883–1885) Πανεπιστήμιο του Τέξας στο Όστιν
• Τα οπτικά του Ευκλείδη Διδακτορική Διατριβή - ΕΑΔΔ
• A History of Greek Mathematics, Τόμος 1
• A History of Greek Mathematics: Τόμος 2
• Advanced Euclidean Geometry
• Methods for Euclidean Geometry.
• Exploring Advanced Euclidean Geometry with GeoGebra.
• Mechanical and Aerospace Engineering, ICMAE2011
• Galileo at Work: His Scientific Biography
• Lattice Models of Polymers
• Excitation Spectra of Square Lattice Antiferromagnets: Theoretical .....
• First-Passage Percolation on the Square Lattice
• Unipotent and Nilpotent Classes in Simple Algebraic Groups and Lie Algebras..

Παραπομπές

• A field guide to the orbifolds (Notes from class on "Geometry and the Imagination" in Minneapolis, with John Conway, Peter Doyle, Jane Gilman and Bill Thurston, on June 17–28, 1991. See also PDF, 2006)
• Tegula Software for visualizing two-dimensional tilings of the plane, sphere and hyperbolic plane, and editing their symmetry groups in orbifold notation