Θεώρημα εξαγώνου του Πάππου

Το θεώρημα εξαγώνου του Πάππου: Τα σημεία X, Y και Z είναι συγγραμμικά στην ευθεία Πάππου. Το εξάγωνο είναι AbCaBc.

Θεώρημα Πάππου: αφινική μορφή
$Ab\parallel aB,Bc\parallel bC\Rightarrow Ac\parallel aC$

Στα μαθηματικά, το Θεώρημα του εξαγώνου του Πάππου (που αποδίδεται στον Πάππο της Αλεξάνδρειας) δηλώνει ότι

• δεδομένου ενός συνόλου συγγραμμικών σημείων $A,B,C,$ και ενός άλλου συνόλου συγγραμμικών σημείων $a,b,c,$ τότε τα σημεία τομής $X,Y,Z$ από τα ζεύγη ευθειών $Ab$ και $aB,Ac$ και $aC,Bc$ και $bC$ είναι συγγραμμικά, που βρίσκονται πάνω στην ευθεία του Πάππου. Τα τρία αυτά σημεία είναι τα σημεία τομής των αντίθετων πλευρών του εξαγώνου $AbCaBc$.

Ισχύει σε ένα προβολικό επίπεδο πάνω από οποιοδήποτε πεδίο, αλλά αποτυγχάνει για προβολικά επίπεδα πάνω από οποιονδήποτε μη αντιμεταθετικό δακτύλιο διαίρεσης. Τα προβολικά επίπεδα στα οποία ισχύει το θεώρημα ονομάζονται επιπεδα του Πάππου.

Αν θεωρήσουμε ένα επίπεδο Πάππου που περιέχει ένα εξάγωνο όπως μόλις περιγράφηκε αλλά με πλευρές $Ab$ και $aB$ παράλληλες και επίσης πλευρές $Bc$ και $bC$ παράλληλες (έτσι ώστε η ευθεία Πάππου $u$ να είναι η ευθεία στο άπειρο), παίρνουμε την αφινική εκδοχή του θεωρήματος του Πάππου που φαίνεται στο δεύτερο διάγραμμα.

Αν η ευθεία Πάππου $u$ και οι ευθείες $g,h$ έχουν ένα κοινό σημείο, προκύπτει η λεγόμενη μικρή εκδοχή του θεωρήματος του Πάππου.

Το δυϊκό αυτό θεώρημα πρόσπτωσης δηλώνει ότι δεδομένου ενός συνόλου συγκλίνουσων ευθειών $A,B,C$ και ενός άλλου συνόλου συγκλίνουσων ευθειών $a,b,c$, τότε οι ευθείες $x,y,z$ που ορίζονται από ζεύγη σημείων που προκύπτουν από ζεύγη τομών $A\cap b$ και $a\cap B,\,A\cap c$ και $a\cap C,\;B\cap c$ και $b\cap C$ είναι συγκλίνουσα. (Συγκλίνουσα σημαίνει ότι οι ευθείες περνούν από ένα σημείο).

Το θεώρημα Πάππου είναι μια ειδική περίπτωση του θεωρήματος του Πασκάλ για την κωνική - η οριακή περίπτωση όταν η κωνική εκφυλίζεται σε 2 ευθείες. Το θεώρημα του Πασκάλ είναι με τη σειρά του μια ειδική περίπτωση του θεωρήματος Κέιλι-Μπάχαραχ.

Η διάταξη Πάππου είναι η διάταξη 9 ευθειών και 9 σημείων που εμφανίζεται στο θεώρημα του Πάππου, με κάθε ευθεία να συναντά 3 από τα σημεία και κάθε σημείο να συναντά 3 ευθείες. Γενικά, η ευθεία του Πάππου δεν περνάει από το σημείο τομής των $ABC$ και $abc$. Αυτή η διαμόρφωση αυτοδιπλώνεται.Δεδομένου ότι, ειδικότερα, οι γραμμές $Bc,bC,XY$ έχουν τις ιδιότητες των γραμμών $x,y,z$ του δυϊκού θεωρήματος, και η συγγραμμικότητα των $X,Y,Z$ είναι ισοδύναμη με τη σύμπτωση των $Bc,bC,XY$, το δυϊκό θεώρημα είναι επομένως ακριβώς το ίδιο με το ίδιο το θεώρημα. Το γράφημα Λεβί της διαμόρφωσης Πάππου είναι το γράφημα Πάππου, ένα διμερές γράφημα κανονικής απόστασης με 18 κορυφές και 27 ακμές.

Απόδειξη: αφινική μορφή

Θεώρημα Πάππου: απόδειξη

Εάν η αφινική μορφή της δήλωσης μπορεί να αποδειχθεί, τότε η προβολική μορφή του θεωρήματος Πάππου αποδεικνύεται, καθώς η επέκταση ενός επιπέδου Πάππου σε ένα προβολικό επίπεδο είναι μοναδική.

Λόγω της παραλληλότητας σε ένα αφινικό επίπεδο πρέπει να διακρίνουμε δύο περιπτώσεις:$g\not \parallel h$ and $g\parallel h$.

Το κλειδί για μια απλή απόδειξη είναι η δυνατότητα εισαγωγής ενός «κατάλληλου» συστήματος συντεταγμένων:

Περίπτωση 1: Οι γραμμές $g,h$ τέμνονται στο σημείο $S=g\cap h$.
Στην περίπτωση αυτή εισάγονται συντεταγμένες, έτσι ώστε $\;S=(0,0),\;A=(0,1),\;c=(1,0)\;$ (βλ. διάγραμμα).

$B,C$ έχουν τις συντεταγμένες $\;B=(0,\gamma ),\;C=(0,\delta ),\;\gamma ,\delta \notin \{0,1\}$.

Από την παραλληλία των ευθειών <$Bc,\;Cb$ προκύπτει $b=({\tfrac {\delta }{\gamma }},0)$ και από την παραλληλία των ευθειών $Ab,Ba$ προκύπτει $a=(\delta ,0)$. Επομένως η ευθεία $Ca$ έχει κλίση $-1$ και είναι παράλληλη με την ευθεία $Ac$.

Case 2: $g\parallel h\$ («μικρό θεώρημα»).
Στην περίπτωση αυτή οι συντεταγμένες επιλέγονται έτσι ώστε $\;c=(0,0),\;b=(1,0),\;A=(0,1),\;B=(\gamma ,1),\;\gamma \neq 0$. Από την παραλληλία των $Ab\parallel Ba$ και $cB\parallel bC$ προκύπτει $\;C=(\gamma +1,1)\;$ και $\;a=(\gamma +1,0)\;$, αντίστοιχα, και τουλάχιστον η παραλληλία $\;Ac\parallel Ca\;$.

Απόδειξη με ομογενείς συντεταγμένες

Επιλέγουμε ομογενείς συντεταγμένες με

$C=(1,0,0),\;c=(0,1,0),\;X=(0,0,1),\;A=(1,1,1)$.

Στις ευθείες $AC,Ac,AX$, οι οποίες δίνονται από τις σχέσεις $x_{2}=x_{3},\;x_{1}=x_{3},\;x_{2}=x_{1}$, ας πάρουμε τα σημεία $B,Y,b$ ως εξής

$B=(p,1,1),\;Y=(1,q,1),\;b=(1,1,r)$

για ορισμένα $p,q,r$. Οι τρεις ευθείες $XB,CY,cb$ είναι < $x_{1}=x_{2}p,\;x_{2}=x_{3}q,\;x_{3}=x_{1}r$, οπότε περνούν από το ίδιο σημείο $a$ αν και μόνο αν $rqp=1$. Η προϋπόθεση για τις τρεις ευθείες $Cb,cB$ και $XY$ με εξισώσεις $x_{2}=x_{1}q,\;x_{1}=x_{3}p,\;x_{3}=x_{2}r$ να διέρχεται από το ίδιο σημείο $Z$ είναι $rpq=1$. Άρα αυτό το τελευταίο σύνολο των τριών ευθειών είναι συγκλίνον αν όλα τα άλλα οκτώ σύνολα είναι, επειδή ο πολλαπλασιασμός είναι αντιμεταθετικός, οπότε $pq=qp$. Ισοδύναμα, τα $X,Y,Z$ είναι συγγραμμικά.

Η παραπάνω απόδειξη δείχνει επίσης ότι για να ισχύει το θεώρημα Πάππου για έναν προβολικό χώρο πάνω από ένα δακτύλιο διαίρεσης είναι τόσο επαρκές όσο και απαραίτητο ο δακτύλιος διαίρεσης να είναι ένα (αντιμεταθετικό) πεδίο. Ο Γερμανός μαθηματικός Gerhard Hessenberg απέδειξε ότι το θεώρημα Πάππου συνεπάγεται το θεώρημα του Ντεσάργκ. Γενικά, το θεώρημα Πάππου ισχύει για κάποιο προβολικό επίπεδο αν και μόνο αν πρόκειται για προβολικό επίπεδο πάνω σε ένα αντιμεταθετικό πεδίο. Τα προβολικά επίπεδα στα οποία δεν ισχύει το θεώρημα Πάππου είναι τα προβολικά επίπεδα Ντεσάργκ πάνω από μη αντιμεταθετικούς δακτυλίους διαίρεσης και τα μη Ντεσάργκιανά επίπεδα.

Η απόδειξη είναι άκυρη αν τα $C,c,X$ τυχαίνει να είναι συγγραμμικά. Σε αυτή την περίπτωση μπορεί να παρασχεθεί μια εναλλακτική απόδειξη, για παράδειγμα, χρησιμοποιώντας μια διαφορετική προβολική αναφορά.

Δυϊκό θεώρημα

Λόγω της αρχής της δυϊκότητας για τα προβολικά επίπεδα, το δυϊκό θεώρημα του Πάππου είναι αληθές:

Εάν 6 ευθείες $A,b,C,a,B,c$ επιλέγονται εναλλάξ από δύο δεσμήματα με κέντρα $G,H$, οι ευθείες

$X:=(A\cap b)(a\cap B),$

$Y:=(c\cap A)(C\cap a),$

$Z:=(b\cap C)(B\cap c)$

είναι συγκλίνουσες, δηλαδή: έχουν ένα κοινό σημείο $U$.
Το αριστερό διάγραμμα δείχνει την προβολική εκδοχή, το δεξιό την αφινική εκδοχή, όπου τα σημεία $G,H$ είναι σημεία στο άπειρο. Αν το σημείο $U$ βρίσκεται στην ευθεία $GH$ τότε έχουμε το «διπλό μικρό θεώρημα» του θεωρήματος Πάππου.

• 
  δυϊκό θεώρημα: προβολική μορφή
• 
  δυϊκό θεώρημα: αφινική μορφή

Αν στην αφινική εκδοχή του δυϊκού «μικρού θεωρήματος» το σημείο $U$ είναι επίσης ένα σημείο στο άπειρο, παίρνουμε το θεώρημα του Τόμσεν, μια δήλωση για 6 σημεία στις πλευρές ενός τριγώνου (βλ. διάγραμμα). Το σχήμα Τόμσεν παίζει ουσιαστικό ρόλο στον συντονισμό ενός αξιωματικά ορισμένου προβολικού επιπέδου. Η απόδειξη του κλεισίματος του σχήματος του Τόμσεν καλύπτεται από την απόδειξη του «μικρού θεωρήματος», που δόθηκε παραπάνω. Υπάρχει όμως και μια απλή άμεση απόδειξη:

Επειδή η δήλωση του θεωρήματος του Τόμσεν (το κλείσιμο του σχήματος) χρησιμοποιεί μόνο τους όρους συνδέω, τέμνω και παράλληλα, η δήλωση είναι αναλλοίωτη ως προς τη συνάφεια και μπορεί κανείς να εισαγάγει συντεταγμένες τέτοιες ώστε $P=(0,0),\;Q=(1,0),\;R=(0,1)$ ( βλ. δεξί διάγραμμα). Το σημείο εκκίνησης της ακολουθίας των χορδών είναι $(0,\lambda ).$ Εύκολα επαληθεύει κανείς τις συντεταγμένες των σημείων που δίνονται στο διάγραμμα, το οποίο δείχνει: το τελευταίο σημείο συμπίπτει με το πρώτο σημείο.

• 
  Σχήμα Τόμσεν (σημεία $\color {red}1,2,3,4,5,6$ του τριγώνου $PQR$) ως δυϊκό θεώρημα του μικρού θεωρήματος του Πάππου (το $U$ είναι επίσης στο άπειρο !).
• 
  Σχήμα Τόμσεν: απόδειξη

Άλλες δηλώσεις του θεωρήματος

Τα τρίγωνα $XcC$ και $BbY$ έχουν προοπτική από τα $A$ και $a$, άρα και από το $Z$.

Εκτός από τους παραπάνω χαρακτηρισμούς του θεωρήματος Πάππου και του δυϊκού του, οι παρακάτω είναι ισοδύναμες δηλώσεις:

• Αν οι έξι κορυφές ενός εξαγώνου βρίσκονται εναλλάξ πάνω σε δύο ευθείες, τότε τα τρία σημεία τομής των ζευγών αντίθετων πλευρών είναι συγγραμμικά.
• Τοποθετημένοι σε έναν πίνακα εννέα σημείων (όπως στο σχήμα και την περιγραφή παραπάνω) και θεωρώντας ότι αξιολογούν ένα μόνιμο, αν οι δύο πρώτες σειρές και οι έξι «διαγώνιες» τριάδες είναι συγγραμμικές, τότε η τρίτη σειρά είναι συγγραμμική.

$\left|{\begin{matrix}A&B&C\\a&b&c\\X&Y&Z\end{matrix}}\right|$

Δηλαδή, αν $\ ABC,abc,AbZ,BcX,CaY,XbC,YcA,ZaB\$ είναι ευθείες, τότε το θεώρημα του Πάππου δηλώνει ότι $XYZ$ πρέπει να είναι ευθεία. Επίσης, ας σημειωθεί ότι η ίδια διατύπωση του πίνακα ισχύει και για τη διπλή μορφή του θεωρήματος όταν $(A,B,C)$ κ.λπ. είναι τριάδες ταυτόχρονων ευθειών.

• Δεδομένων τριών διαφορετικών σημείων σε κάθε μία από δύο διαφορετικές ευθείες, αν αντιστοιχίσετε κάθε σημείο σε μία από τις ευθείες με ένα από την άλλη ευθεία, τότε οι ενώσεις των σημείων που δεν έχουν αντιστοιχιστεί θα συναντηθούν σε (αντίθετα) ζεύγη σε σημεία κατά μήκος μιας ευθείας.
• Αν δύο τρίγωνα είναι προοπτικά με τουλάχιστον δύο διαφορετικούς τρόπους, τότε είναι προοπτικά με τρεις τρόπους.
• Αν οι $\;AB,CD,\;$ και $EF$ είναι συγκλίνουσες και οι $DE,FA,$ και $BC$ είναι συγκλίνουσες , τότε οι $AD,BE,$ και $CF$ είναι συγκλίνουσες.

Προέλευση

Στην παλαιότερη γνωστή μορφή του, το Θεώρημα του Πάππου είναι οι προτάσεις 138, 139, 141 και 143 του Βιβλίου VII της Συλλογής του Πάππου. Πρόκειται για τα Λήμματα XII, XIII, XV και XVII στο μέρος του Βιβλίου VII που αποτελείται από λήμματα στο πρώτο από τα τρία βιβλία των Πορισμάτων του Ευκλείδη.

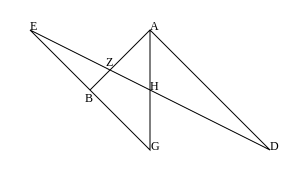
Τα λήμματα αποδεικνύονται με βάση αυτό που σήμερα είναι γνωστό ως ο λόγος διασταύρωσης τεσσάρων συγγραμμικών σημείων. Χρησιμοποιούνται τρία προηγούμενα λήμματα. Το πρώτο από αυτά, το Λήμμα ΙΙΙ, έχει το παρακάτω διάγραμμα (το οποίο χρησιμοποιεί τα γράμματα του Πάππου, με G για το Γ, D για το Δ, J για το Θ και L για το Λ).

Εδώ τρεις συγκλίνουσες ευθείες, AB, AG και AD, τέμνονται από δύο ευθείες, JB και JE, οι οποίες συμπίπτουν στο σημείο J. Επίσης η KL χαράσσεται παράλληλα με την AZ. Τότε

KJ : JL :: (KJ : AG & AG : JL) :: (JD : GD & BG : JB).

Αυτές οι αναλογίες θα μπορούσαν να γραφούν σήμερα ως εξισώσεις:

KJ/JL = (KJ/AG)(AG/JL) = (JD/GD)(BG/JB).

Ο τελευταίος σύνθετος λόγος (δηλαδή JD : GD & BG : JB) είναι γνωστός σήμερα ως ο διπλός λόγος των συγγραμμικών σημείων J, G, D και B με αυτή τη σειρά- συμβολίζεται σήμερα με (J, G; D, B). Έτσι δείξαμε ότι αυτό είναι ανεξάρτητο από την επιλογή της συγκεκριμένης ευθείας JD που τέμνει τις τρεις ευθείες που συμπίπτουν στο Α. Συγκεκριμένα

(J, G; D, B) = (J, Z; H, E).

Δεν έχει σημασία σε ποια πλευρά του Α πέφτει η ευθεία JE. Συγκεκριμένα, η κατάσταση μπορεί να είναι όπως στο επόμενο διάγραμμα, το οποίο είναι το διάγραμμα για το Λήμμα Χ.

Όπως και προηγουμένως, έχουμε (J, G; D, B) = (J, Z; H, E). Ο Πάππος δεν το αποδεικνύει ρητά αυτό- αλλά το Λήμμα Χ είναι ένα αντίστροφο, δηλαδή ότι αν αυτές οι δύο διασταυρούμενες αναλογίες είναι ίδιες και οι ευθείες BE και DH τέμνονται στο Α, τότε τα σημεία G, A και Z πρέπει να είναι συγγραμμικά.

Αυτό που δείξαμε αρχικά μπορεί να γραφτεί ως (J, ∞; K, L) = (J, G; D, B), με το ∞ να παίρνει τη θέση της (ανύπαρκτης) τομής των JK και AG. Ο Πάππος το δείχνει αυτό, στην πραγματικότητα, στο Λήμμα ΧΙ, του οποίου το διάγραμμα, ωστόσο, έχει διαφορετικά γράμματα:

Αυτό που δείχνει ο Πάππος είναι DE.ZH : EZ.HD :: GB : BE, το οποίο μπορούμε να γράψουμε ως εξής

(D, Z; E, H) = (∞, B; E, G).

Το διάγραμμα του Λήμματος XII είναι:

Το διάγραμμα για το Λήμμα XIII είναι το ίδιο, αλλά οι BA και DG, εκτεταμένες, συναντώνται στο N. Σε κάθε περίπτωση, θεωρώντας ότι οι ευθείες που διέρχονται από το G κόβονται από τις τρεις ευθείες που διέρχονται από το A, (και δεχόμενοι ότι οι εξισώσεις των διπλών λόγων παραμένουν έγκυρες μετά την αντιμετάθεση των καταχωρήσεων) έχουμε από το Λήμμα III ή XI

(G, J; E, H) = (G, D; ∞ Z).

Θεωρώντας ότι οι ευθείες που διέρχονται από το D κόβονται από τις τρεις ευθείες που διέρχονται από το B, έχουμε

(L, D; E, K) = (G, D; ∞ Z).

Συνεπώς (E, H; J, G) = (E, K; D, L), οπότε σύμφωνα με το Λήμμα X, τα σημεία H, M και K είναι συγγραμμικά. Δηλαδή, τα σημεία τομής των ζευγών των αντίθετων πλευρών του εξαγώνου ADEGBZ είναι συγγραμμικά.

Δημοσιεύσεις

• Dembowski, Peter (1968), Finite geometries, Ergebnisse der Mathematik und ihrer Grenzgebiete, 44, Berlin: Springer, ISBN 3-540-61786-8, https://archive.org/details/finitegeometries0000demb 
• Euclid (1956). The Thirteen Books of Euclid's Elements, Translated from the Text of Heiberg, with Introduction and Commentary. 1 (Books I and II). Μτφρ. Heath, Thomas L. (Reprint of 2nd (1925) έκδοση). Dover.  On-line text at archive.org
• Bourke, Paul (Ιουλίου 1997). «Calculating the area and centroid of a polygon». 
• Simon Plouffe (1998). «The Computation of Certain Numbers Using a Ruler and Compass». Journal of Integer Sequences 1: 13. ISSN 1530-7638. Bibcode: 1998JIntS...1...13P. http://www.cs.uwaterloo.ca/journals/JIS/compass.html. 
• Pappi (1660). Mathematicae collectiones (στα Λατινικά). ex typographia HH. de Duccijs. 
• Brannan, David A.; Esplen, Matthew F.; Gray, Jeremy J. (1998), Geometry, Cambridge University Press, ISBN 0-521-59787-0 
• Coxeter, H. S. M. (1969), Introduction to Geometry, New York: John Wiley & Sons, ISBN 0-471-50458-0 
• Boyer, Carl B. (2004), History of Analytic Geometry, Dover, ISBN 978-0-486-43832-0, https://books.google.com/books?id=2T4i5fXZbOYC 
• Oakley, C. O., Ph.D. (1944), An Outline of the Calculus, New York: Barnes & Noble 
• Protter, Murray H.; Morrey, Charles B. Jr. (1970), College Calculus with Analytic Geometry (2nd έκδοση), Reading: Addison-Wesley 

Δείτε επίσης

• Πραγματικό προβολικό επίπεδο
• Στοιχεία του Ευκλείδη
• Ευκλείδειος χώρος
• Καρτεσιανό σύστημα συντεταγμένων
• Μιγαδικός αριθμός
• τοπολογικος ισομορφισμός
• Παραβολή (γεωμετρία)
• Προβολή (γραμμική άλγεβρα)
• Πάππος ο Αλεξανδρεύς
• Αμπού αλ Ουάφα
• Τετραγωνισμός παραβολής
• Διαβήτης (όργανο)
• Διπλασιασμός του κύβου
• Προβολική γεωμετρία
• Υπερβολή (γεωμετρία)
• Μη αντιμεταθετική αλγεβρική γεωμετρία
• Κωνική τομή
• Παραλληλόγραμμο
• Θεώρημα Κέιλι-Μπάχαραχ

Εξωτερικοί σύνδεσμοι

• English - Greek Dictionary of Pure and Applied Mathematics Εθνικό Μετσόβιο Πολυτεχνείο
• Αγγλοελληνικό Λεξικό Μαθηματικής Ορολογίας - Πανεπιστήμιο Κύπρου
• Ευκλείδεια Γεωμετρία - Πανελλήνιο Σχολικό Δίκτυο
• Euclid’s elements of geometry - The Greek text of J.L. Heiberg (1883–1885) Πανεπιστήμιο του Τέξας στο Όστιν
• Τα οπτικά του Ευκλείδη Διδακτορική Διατριβή - ΕΑΔΔ
• “Αρχιμήδους Βιβλίο Λημμάτων” – Πραγματεία του Νικολάου Λ. Κεχρή Ανοιχτή βιβλιοθήκη
• Virtual book about Archimedes Chris Rorres - Drexel University
• A History of Greek Mathematics, Τόμος 1
• A History of Greek Mathematics: Τόμος 2
• Advanced Euclidean Geometry
• Methods for Euclidean Geometry.
• Collineations and Conic Sections: An Introduction to Projective Geometry in .......Pappus's hexagon theorem..page55
• Projective Geometry: Exploring Projective Geometry in Computer Vision... Pappus's hexagon theorem
• Concise Encyclopedia of Mathematics..Pappus's hexagon theorem.. page 361
• Commutative Algebra Methods for Coding Theory.Pappus's hexagon theorem...page 58 .
• Topics in Elementary Geometry.. Theory.Pappus's hexagon theorem... page 96...
• Illustrated Glossary for School Mathematics ...Pappus's hexagon theorem.....page 324
• Unipotent and Nilpotent Classes in Simple Algebraic Groups and Lie Algebras..

Πηγές

• Coxeter, Harold Scott MacDonald (1969), Introduction to Geometry (2nd έκδοση), New York: John Wiley & Sons, ISBN 978-0-471-50458-0 
• Cronheim, A. (1953), «A proof of Hessenberg's theorem», Proceedings of the American Mathematical Society 4 (2): 219–221, doi:10.2307/2031794 
• Dembowski, Peter (1968), Finite Geometries, Berlin: Springer-Verlag 
• Heath, Thomas (1981), A History of Greek Mathematics, New York: Dover Publications 
• Hessenberg, Gerhard (1905), «Beweis des Desarguesschen Satzes aus dem Pascalschen», Mathematische Annalen (Berlin / Heidelberg: Springer) 61 (2): 161–172, doi:10.1007/BF01457558, ISSN 1432-1807 
• Hultsch, Fridericus (1877), Pappi Alexandrini Collectionis Quae Supersunt, Berlin 
• Kline, Morris (1972), Mathematical Thought From Ancient to Modern Times, New York: Oxford University Press 
• Pambuccian, Victor; Schacht, Celia (2019), «The axiomatic destiny of the theorems of Pappus and Desargues», στο: Dani, S. G.; Papadopoulos, A., επιμ., Geometry in history, Springer, σελ. 355–399, ISBN 978-3-030-13611-6 
• Whicher, Olive (1971), Projective Geometry, Rudolph Steiner Press, ISBN 0-85440-245-4