Τετραγωνισμός παραβολής

Ο τετραγωνισμός της παραβολής είναι μια γεωμετρική πραγματεία, γραμμένη από τον Αρχιμήδη τον 3ο αιώνα π.Χ. και απευθύνεται στον Αλεξανδρινό φίλο του Δοσίθεο. Περιέχει 24 προτάσεις σχετικά με τις παραβολές, με αποκορύφωμα δύο αποδείξεις που δείχνουν ότι το εμβαδόν ενός παραβολικού τμήματος (η περιοχή που περικλείεται από μια παραβολή και μια ευθεία) είναι ${\tfrac {4}{3}}$ εκείνο ενός συγκεκριμένου εγγεγραμμένου τριγώνου.

Πρόκειται για ένα από τα πιο γνωστά έργα του Αρχιμήδη, κυρίως για την έξυπνη χρήση της μεθόδου της εξάντλησης και στο δεύτερο μέρος μιας γεωμετρικής σειράς. Ο Αρχιμήδης αναλύει το εμβαδόν σε έναν άπειρο αριθμό τριγώνων, τα εμβαδά των οποίων σχηματίζουν μια γεωμετρική πρόοδο^[1], στη συνέχεια υπολογίζει το άθροισμα της γεωμετρικής σειράς που προκύπτει και αποδεικνύει ότι είναι το εμβαδόν του παραβολικού τμήματος. Αυτή ήταν η πιο εξελιγμένη χρήση ενός reductio ad absurdum (Εις άτοπον απαγωγή) επιχειρήματος στα αρχαία ελληνικά μαθηματικά, και η λύση του Αρχιμήδη παρέμεινε αξεπέραστη μέχρι την ανάπτυξη του ολοκληρωτικού λογισμού τον 17ο αιώνα, καθώς τη διαδέχθηκε ο τύπος τετραγωνισμού του Καβαλιέρη^[2].

Κύριο θεώρημα

Ένα παραβολικό τμήμα είναι η περιοχή που οριοθετείται από μια παραβολή και μια ευθεία. Για να βρει το εμβαδόν ενός παραβολικού τμήματος, ο Αρχιμήδης θεωρεί ένα ορισμένο εγγεγραμμένο τρίγωνο. Η βάση αυτού του τριγώνου είναι η δεδομένη χορδή της παραβολής, και η τρίτη κορυφή είναι το σημείο της παραβολής τέτοιο ώστε η εφαπτομένη της παραβολής στο σημείο αυτό να είναι παράλληλη με τη χορδή. Η Πρόταση 1 του έργου αναφέρει ότι μια ευθεία από την τρίτη κορυφή που χαράσσεται παράλληλα στον άξονα διαιρεί τη χορδή σε ίσα τμήματα. Το κύριο θεώρημα ισχυρίζεται ότι το εμβαδόν του παραβολικού τμήματος είναι ${\tfrac {4}{3}}$ αυτό του εγγεγραμμένου τριγώνου.

Δομή του κειμένου

Η πρώτη απόδειξη του Αρχιμήδη για το εμβαδόν ενός παραβολικού τμήματος.

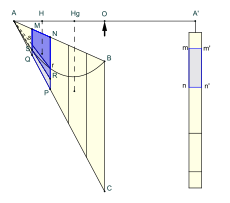
Κωνικές τομές, όπως η παραβολή, ήταν ήδη γνωστές στην εποχή του Αρχιμήδη χάρη στον Μέναιχμο έναν αιώνα νωρίτερα. Ωστόσο, πριν από την έλευση του διαφορικού λογισμού και του ολοκληρώματος, δεν υπήρχαν εύκολα μέσα για να βρεθεί το εμβαδόν μιας κωνικής τομής. Ο Αρχιμήδης παρέχει την πρώτη τεκμηριωμένη λύση σε αυτό το πρόβλημα, εστιάζοντας ειδικά στο εμβαδόν που οριοθετείται από μια παραβολή και μια χορδή^[3].

Ο Αρχιμήδης δίνει δύο αποδείξεις του κύριου θεωρήματος: η μία χρησιμοποιεί αφηρημένη μηχανική και η άλλη καθαρή γεωμετρία. Στην πρώτη απόδειξη, ο Αρχιμήδης θεωρεί έναν μοχλό σε ισορροπία υπό την επίδραση της βαρύτητας, με σταθμισμένα τμήματα μιας παραβολής και ενός τριγώνου αναρτημένα κατά μήκος των βραχιόνων του μοχλού σε συγκεκριμένες αποστάσεις από το σημείο στήριξης.^[4]Όταν το κέντρο βάρους του τριγώνου είναι γνωστό, η ισορροπία του μοχλού δίνει το εμβαδόν της παραβολής ως προς το εμβαδόν του τριγώνου που έχει την ίδια βάση και ίσο ύψος.^[5] Ο Αρχιμήδης εδώ αποκλίνει από τη διαδικασία που βρίσκεται στο Περί ισορροπίας των επιπέδων, καθώς έχει τα κέντρα βάρους σε επίπεδο κάτω από αυτό της ισορροπίας.^[6] Η δεύτερη και πιο διάσημη απόδειξη χρησιμοποιεί καθαρή γεωμετρία, και συγκεκριμένα το άθροισμα μιας γεωμετρικής σειράς.

Από τις είκοσι τέσσερις προτάσεις, οι τρεις πρώτες παρατίθενται χωρίς απόδειξη από τα Στοιχεία των Κωνικών του Ευκλείδη (ένα χαμένο έργο του Ευκλείδη για τις κωνικές τομές). Οι προτάσεις 4 και 5 καθορίζουν στοιχειώδεις ιδιότητες της παραβολής. Οι προτάσεις 6-17 δίνουν τη μηχανική απόδειξη του κύριου θεωρήματος- οι προτάσεις 18-24 παρουσιάζουν τη γεωμετρική απόδειξη.

Γεωμετρική απόδειξη

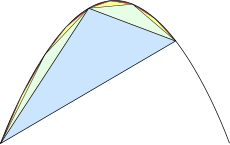
Διαίρεση του παραβολικού τμήματος

Η κύρια ιδέα της απόδειξης είναι η διαίρεση του παραβολικού τμήματος σε άπειρα τρίγωνα, όπως φαίνεται στο σχήμα στα δεξιά. Κάθε ένα από αυτά τα τρίγωνα εγγράφεται στο δικό του παραβολικό τμήμα με τον ίδιο τρόπο που το μπλε τρίγωνο εγγράφεται στο μεγάλο τμήμα.

Εμβαδά των τριγώνων

Στις προτάσεις 18 έως 21, ο Αρχιμήδης αποδεικνύει ότι το εμβαδόν κάθε πράσινου τριγώνου είναι ${\tfrac {1}{8}}$ το εμβαδόν του μπλε τριγώνου, έτσι ώστε τα δύο πράσινα τρίγωνα μαζί να έχουν άθροισμα ${\tfrac {1}{4}}$ το εμβαδόν του μπλε τριγώνου. Από μια σύγχρονη άποψη, αυτό συμβαίνει επειδή το πράσινο τρίγωνο έχει ${\tfrac {1}{2}}$ το πλάτος και ${\tfrac {1}{4}}$ το ύψος του μπλε τριγώνου:^[7].

Ακολουθώντας το ίδιο επιχείρημα, κάθε ένα από τα $4$ κίτρινα τρίγωνα έχει ${\tfrac {1}{8}}$ το εμβαδόν ενός πράσινου τριγώνου ή ${\tfrac {1}{64}}$ το εμβαδόν του μπλε τριγώνου, αθροίζοντας σε ${\tfrac {4}{64}}={\tfrac {1}{16}}$ το εμβαδόν του μπλε τριγώνου, κάθε ένα από τα $2^{3}=8$ κόκκινα τρίγωνα έχει ${\tfrac {1}{8}}$ το εμβαδόν ενός κίτρινου τριγώνου, αθροίζοντας σε ${\tfrac {2^{3}}{8^{3}}}={\tfrac {1}{64}}$ το εμβαδόν του μπλε τριγώνου- κ.λπ. Χρησιμοποιώντας τη μέθοδο της εξάντλησης, προκύπτει ότι το συνολικό εμβαδόν του παραβολικού τμήματος δίνεται από τη σχέση

{\text{Area}}\;=\;T\,+\,{\frac {1}{4}}T\,+\,{\frac {1}{4^{2}}}T\,+\,{\frac {1}{4^{3}}}T\,+\,\cdots .

Εδώ το Τ αντιπροσωπεύει το εμβαδόν του μεγάλου μπλε τριγώνου, ο δεύτερος όρος αντιπροσωπεύει το συνολικό εμβαδόν των δύο πράσινων τριγώνων, ο τρίτος όρος αντιπροσωπεύει το συνολικό εμβαδόν των τεσσάρων κίτρινων τριγώνων κ.ο.κ. Αυτό απλοποιείται δίνοντας

{\text{Area}}\;=\;\left(1\,+\,{\frac {1}{4}}\,+\,{\frac {1}{16}}\,+\,{\frac {1}{64}}\,+\,\cdots \right)T.

Άθροισμα της σειράς

Η απόδειξη του Αρχιμήδη ότι $1 / 4 + 1 / 16 + 1 / 64 + \dots = 1 / 3$

Για να ολοκληρωθεί η απόδειξη, ο Αρχιμήδης επισημαίνει ότι

1\,+\,{\frac {1}{4}}\,+\,{\frac {1}{16}}\,+\,{\frac {1}{64}}\,+\,\cdots \;=\;{\frac {4}{3}}.

Ο παραπάνω τύπος είναι μια γεωμετρική σειρά - κάθε διαδοχικός όρος είναι το ένα τέταρτο του προηγούμενου όρου. Στα σύγχρονα μαθηματικά, ο τύπος αυτός είναι μια ειδική περίπτωση του τύπου αθροίσματος για μια γεωμετρική σειρά.

Ο Αρχιμήδης αξιολογεί το άθροισμα χρησιμοποιώντας μια εντελώς γεωμετρική μέθοδο,^[8] η οποία απεικονίζεται στη διπλανή εικόνα. Η εικόνα αυτή δείχνει ένα μοναδιαίο τετράγωνο το οποίο έχει τεμαχιστεί σε άπειρα μικρότερα τετράγωνα. Κάθε διαδοχικό μωβ τετράγωνο έχει το ένα τέταρτο του εμβαδού του προηγούμενου τετραγώνου, με το συνολικό μωβ εμβαδόν να είναι το άθροισμα

{\frac {1}{4}}\,+\,{\frac {1}{16}}\,+\,{\frac {1}{64}}\,+\,\cdots .

Ωστόσο, τα μωβ τετράγωνα είναι συγγραμμικά με οποιοδήποτε σύνολο κίτρινων τετραγώνων και έτσι καλύπτουν ${\tfrac {1}{3}}$ του εμβαδού του μοναδιαίου τετραγώνου. Προκύπτει ότι η παραπάνω σειρά έχει άθροισμα ${\tfrac {4}{3}}$ (αφού $1+{\tfrac {1}{3}}={\tfrac {4}{3}}$ ).

Δημοσιεύσεις

Bell, John L. (1999). The Art of the Intelligible: An Elementary Survey of Mathematics in its Conceptual Development. Kluwer. ISBN 0-7923-5972-0.
Euclid (1956). The Thirteen Books of Euclid's Elements, Translated from the Text of Heiberg, with Introduction and Commentary. 1 (Books I and II). Μτφρ. Heath, Thomas L. (Reprint of 2nd (1925) έκδοση). Dover. On-line text at archive.org

Ajose, Sunday and Roger Nelsen (June 1994). «Proof without Words: Geometric Series». Mathematics Magazine 67 (3): 230. doi:10.2307/2690617.
Ancora, Luciano (2014). «Quadrature of the parabola with the square pyramidal number». Archimede 66 (3). https://www.zentralblatt-math.org/matheduc/en/?q=an%3A2016f.01058.
Bressoud, David M. (2006). A Radical Approach to Real Analysis (2nd έκδοση). Mathematical Association of America. ISBN 0-88385-747-2. .
Dijksterhuis, E.J. (1987) "Archimedes", Princeton U. Press ISBN 0-691-08421-1
Edwards Jr., C. H. (1994). The Historical Development of the Calculus (3rd έκδοση). Springer. ISBN 0-387-94313-7. .
Heath, Thomas L. (2011). The Works of Archimedes (2nd έκδοση). CreateSpace. ISBN 978-1-4637-4473-1.
Simmons, George F. (2007). Calculus Gems. Mathematical Association of America. ISBN 978-0-88385-561-4. .
Stein, Sherman K. (1999). Archimedes: What Did He Do Besides Cry Eureka?. Mathematical Association of America. ISBN 0-88385-718-9.
Stillwell, John (2004). Mathematics and its History (2nd έκδοση). Springer. ISBN 0-387-95336-1. .
Swain, Gordon and Thomas Dence (April 1998). «Archimedes' Quadrature of the Parabola Revisited». Mathematics Magazine 71 (2): 123–30. doi:10.2307/2691014.
Wilson, Alistair Macintosh (1995). The Infinite in the Finite. Oxford University Press. ISBN 0-19-853950-9. .

Δείτε επίσης

Field Arithmetic
Βικιπαίδεια:Εγχειρίδιο μορφής/Μαθηματικά (Περιέχει και τα αγγλοελληνικά Λεξικά Μαθηματικής Ορολογίας)
Πραγματικό προβολικό επίπεδο
Στοιχεία του Ευκλείδη
Ευκλείδειος χώρος
Καρτεσιανό σύστημα συντεταγμένων
Μιγαδικός αριθμός
τοπολογικος ισομορφισμός
Παραβολή (γεωμετρία)
Προβολή (γραμμική άλγεβρα)
Πυθαγόρειο θεώρημα
Διανυσματική προβολή
Διαβήτης (όργανο)
Ημικύκλιο
Ορθόκεντρο τριγώνου
Αρχιμήδεια ιδιότητα
Εγγεγραμμένος και Παρεγγεγραμμένοι κύκλοι τριγώνου
Μιγαδική ανάλυση
Μιγαδικό επίπεδο
Διανυσματική προβολή
High performance algorithms for reduction to condensed (Hessenberg, tridiagonal, bidiagonal) form

Εξωτερικοί σύνδεσμοι

Παραπομπές

↑ Swain, Gordon; Dence, Thomas (1998). «Archimedes' Quadrature of the Parabola Revisited». Mathematics Magazine 71 (2): 123–130. doi:10.2307/2691014. ISSN 0025-570X. https://www.jstor.org/stable/2691014.
↑ Cusick, Larry W. (2008). «Archimedean Quadrature Redux». Mathematics Magazine 81 (2): 83–95. doi:10.1080/0025570X.2008.11953535. ISSN 0025-570X. https://www.jstor.org/stable/27643090.
↑ Towne, R. (2018). «Archimedes in the Classroom». Master's Thesis John Carroll University. https://collected.jcu.edu/mastersessays/91.
↑ «Quadrature of the parabola, Introduction». web.calstatela.edu. Ανακτήθηκε στις 3 Ιουλίου 2021.
↑ «The Illustrated Method of Archimedes». Scribd (στα Αγγλικά). Ανακτήθηκε στις 3 Ιουλίου 2021.
↑ Dijksterhuis, E. J. (1987). «Quadrature of the Parabola» (στα Αγγλικά). Archimedes. σελίδες 336–345.
↑ The green triangle has ${\tfrac {1}{2}}$ the width of blue triangle by construction. The statement about the height follows from the geometric properties of a parabola, and is easy to prove using modern analytic geometry.
↑ Strictly speaking, Archimedes evaluates the partial sums of this series, and uses the Archimedean property to argue that the partial sums become arbitrarily close to ${\tfrac {4}{3}}$ . This is logically equivalent to the modern idea of summing an infinite series.

Casselman, Bill. «Archimedes' quadrature of the parabola». Αρχειοθετήθηκε από το πρωτότυπο στις 4 Φεβρουαρίου 2012. Full text, as translated by T.L. Heath.
Xavier University Department of Mathematics and Computer Science. «Archimedes of Syracuse». Αρχειοθετήθηκε από το πρωτότυπο στις 13 Ιανουαρίου 2016. . Text of propositions 1–3 and 20–24, with commentary.
http://planetmath.org/ArchimedesCalculus

[1] Swain, Gordon; Dence, Thomas (1998). «Archimedes' Quadrature of the Parabola Revisited». Mathematics Magazine 71 (2): 123–130. doi:10.2307/2691014. ISSN 0025-570X. https://www.jstor.org/stable/2691014.

[2] Cusick, Larry W. (2008). «Archimedean Quadrature Redux». Mathematics Magazine 81 (2): 83–95. doi:10.1080/0025570X.2008.11953535. ISSN 0025-570X. https://www.jstor.org/stable/27643090.

[3] Towne, R. (2018). «Archimedes in the Classroom». Master's Thesis John Carroll University. https://collected.jcu.edu/mastersessays/91.

[4] «Quadrature of the parabola, Introduction». web.calstatela.edu. Ανακτήθηκε στις 3 Ιουλίου 2021.

[5] «The Illustrated Method of Archimedes». Scribd (στα Αγγλικά). Ανακτήθηκε στις 3 Ιουλίου 2021.

[6] Dijksterhuis, E. J. (1987). «Quadrature of the Parabola» (στα Αγγλικά). Archimedes. σελίδες 336–345.

[7] The green triangle has ${\tfrac {1}{2}}$ the width of blue triangle by construction. The statement about the height follows from the geometric properties of a parabola, and is easy to prove using modern analytic geometry.

[8] Strictly speaking, Archimedes evaluates the partial sums of this series, and uses the Archimedean property to argue that the partial sums become arbitrarily close to ${\tfrac {4}{3}}$ . This is logically equivalent to the modern idea of summing an infinite series.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]