Πυθαγόρεια τριγωνομετρική ταυτότητα

Η Πυθαγόρεια τριγωνομετρική ταυτότητα, που ονομάζεται επίσης απλά πυθαγόρεια ταυτότητα, είναι μια ταυτότητα που εκφράζει το πυθαγόρειο θεώρημα σε όρους τριγωνομετρικών συναρτήσεων. Μαζί με τον τύπο του αθροίσματος των γωνιών, είναι μία από τις βασικές σχέσεις μεταξύ των συναρτήσεων ημιτόνου και συνημιτόνου.

Η ταυτότητα είναι η εξής

$\sin ^{2}\theta +\cos ^{2}\theta =1.$

Κατά κανόνα, $\sin ^{2}\theta$ σημαίνει ${\textstyle (\sin \theta )^{2}}$.

Αποδείξεις και οι σχέσεις τους με το Πυθαγόρειο θεώρημα

Παρόμοια ορθογώνια τρίγωνα που δείχνουν το ημίτονο και το συνημίτονο της γωνίας θ

Απόδειξη βασισμένη σε ορθογώνια τρίγωνα

Κάθε όμοιο τρίγωνο έχει την ιδιότητα ότι αν επιλέξουμε την ίδια γωνία σε όλα, ο λόγος των δύο πλευρών που ορίζουν τη γωνία είναι ο ίδιος, ανεξάρτητα από το ποιο όμοιο τρίγωνο επιλέγεται, ανεξάρτητα από το πραγματικό του μέγεθος: οι λόγοι εξαρτώνται από τις τρεις γωνίες, όχι από τα μήκη των πλευρών. Ως εκ τούτου, για οποιοδήποτε από τα όμοια ορθογώνια τρίγωνα του σχήματος, ο λόγος της οριζόντιας πλευράς του προς την υποτείνουσα είναι ο ίδιος, δηλαδή cos θ.

Οι στοιχειώδεις ορισμοί των συναρτήσεων ημιτόνου και συνημιτόνου ως προς τις πλευρές ενός ορθογωνίου τριγώνου είναι:

$\sin \theta ={\frac {\mathrm {opposite} }{\mathrm {hypotenuse} }}={\frac {b}{c}}$

$\cos \theta ={\frac {\mathrm {adjacent} }{\mathrm {hypotenuse} }}={\frac {a}{c}}$

Η πυθαγόρεια ταυτότητα προκύπτει από τον τετραγωνισμό και των δύο παραπάνω ορισμών και την πρόσθεση- η αριστερή πλευρά της ταυτότητας γίνεται τότε

${\frac {\mathrm {opposite} ^{2}+\mathrm {adjacent} ^{2}}{\mathrm {hypotenuse} ^{2}}}$

η οποία σύμφωνα με το Πυθαγόρειο θεώρημα είναι ίση με 1. Ο ορισμός αυτός ισχύει για όλες τις γωνίες, λόγω του ορισμού του ορισμού $x=\cos \theta$ και $y=\sin \theta$ για τον μοναδιαίο κύκλο και συνεπώς $x=c\cos \theta$ και $y=c\sin \theta$ για έναν κύκλο ακτίνας c και αντικατοπτρίζοντας το τρίγωνό μας στον άξονα y και θέτοντας $a=x$ and $b=y$.

Παρόμοια ορθογώνια τρίγωνα που απεικονίζουν την εφαπτομένη και την δευτερεύουσα τριγωνομετρική συνάρτηση.

Μπορούμε επίσης να χρησιμοποιήσουμε τις ταυτότητες που βρίσκονται στην Τριγωνομετρική συμμετρία, τις μετατοπίσεις και την περιοδικότητα. Χρησιμοποιώντας ταυτότητες περιοδικότητας, μπορούμε να πούμε ότι αν ο τύπος είναι αληθής για -π < θ ≤ π τότε είναι αληθής για όλα τα πραγματικά θ. Στη συνέχεια αποδεικνύουμε την ταυτότητα στο διάστημα π/2 < θ ≤ π,, για να το κάνουμε αυτό αφήνουμε t = θ - π/2, το t θα είναι τώρα στο διάστημα 0 < t ≤ π/2. Στη συνέχεια μπορούμε να χρησιμοποιήσουμε τετραγωνισμένες εκδοχές ορισμένων βασικών ταυτοτήτων μετατόπισης (ο τετραγωνισμός αφαιρεί βολικά τα μείον πρόσημα):

$\sin ^{2}\theta +\cos ^{2}\theta =\sin ^{2}\left(t+{\tfrac {1}{2}}\pi \right)+\cos ^{2}\left(t+{\tfrac {1}{2}}\pi \right)=\cos ^{2}t+\sin ^{2}t=1.$

Το μόνο που απομένει είναι να το αποδείξουμε για -π < θ < 0; αυτό μπορεί να γίνει με τον τετραγωνισμό των ταυτοτήτων συμμετρίας για να πάρουμε

$\sin ^{2}\theta =\sin ^{2}(-\theta ){\text{ and }}\cos ^{2}\theta =\cos ^{2}(-\theta ).$

Σχετικές ταυτότητες

Τριγωνομετρικές συναρτήσεις και τα αντίστροφά τους στον μοναδιαίο κύκλο. Το Πυθαγόρειο θεώρημα εφαρμοσμένο στο μπλε τρίγωνο δείχνει την ταυτότητα 1 + cot² θ' = csc²&thinsp, θ, και εφαρμοσμένη στο κόκκινο τρίγωνο δείχνει ότι 1 + tan² θ = sec² θ.

Οι ταυτότητες

$1+\tan ^{2}\theta =\sec ^{2}\theta$

και

$1+\cot ^{2}\theta =\csc ^{2}\theta$

ονομάζονται επίσης πυθαγόρειες τριγωνομετρικές ταυτότητες. Αν το ένα σκέλος ενός ορθογωνίου τριγώνου έχει μήκος 1, τότε η εφαπτομένη της γωνίας που εφάπτεται σε αυτό το σκέλος είναι το μήκος του άλλου σκέλους και η δευτερεύουσα της γωνίας είναι το μήκος της υποτείνουσας.

$\tan \theta ={\frac {b}{a}},$

και:

$\sec \theta ={\frac {c}{a}}.$

Με αυτόν τον τρόπο, αυτή η τριγωνομετρική ταυτότητα που περιλαμβάνει την εφαπτομένη και τη δευτερεύουσα προκύπτει από το Πυθαγόρειο θεώρημα. Η γωνία απέναντι από το πόδι μήκους 1 (η γωνία αυτή μπορεί να χαρακτηριστεί φ = π/2 - θ) έχει συνεφαπτομένη ίση με το μήκος του άλλου σκέλους και συντέμνουσα ίση με το μήκος της υποτείνουσας. Με αυτόν τον τρόπο, αυτή η τριγωνομετρική ταυτότητα που περιλαμβάνει την συνεφαπτομένη και την συντέμνουσα προκύπτει επίσης από το Πυθαγόρειο θεώρημα.

Στον ακόλουθο πίνακα δίνονται οι ταυτότητες με τον παράγοντα ή το διαιρέτη που τις συνδέει με την κύρια ταυτότητα.

Αρχική ταυτότητα	Διαιρέτης	Εξίσωση διαιρέτη	Παράγωγη ταυτότητα	Παράγωγη ταυτότητα (εναλλακτική)
$\sin ^{2}\theta +\cos ^{2}\theta =1$	$\cos ^{2}\theta$	${\frac {\sin ^{2}\theta }{\cos ^{2}\theta }}+{\frac {\cos ^{2}\theta }{\cos ^{2}\theta }}={\frac {1}{\cos ^{2}\theta }}$	$\tan ^{2}\theta +1=\sec ^{2}\theta$	${\begin{aligned}\sec ^{2}\theta -\tan ^{2}\theta =1\\(\sec \theta -\tan \theta )(\sec \theta +\tan \theta )=1\\\end{aligned}}$
	$\sin ^{2}\theta$	${\frac {\sin ^{2}\theta }{\sin ^{2}\theta }}+{\frac {\cos ^{2}\theta }{\sin ^{2}\theta }}={\frac {1}{\sin ^{2}\theta }}$	$1+\cot ^{2}\theta =\csc ^{2}\theta$	${\begin{aligned}\csc ^{2}\theta -\cot ^{2}\theta =1\\(\csc \theta -\cot \theta )(\csc \theta +\cot \theta )=1\\\end{aligned}}$

Απόδειξη με χρήση του μοναδιαίου κύκλου

Σημείο P(x,y) στον κύκλο μοναδιαίας ακτίνας σε αμβλεία γωνία θ > π/2

Συνάρτηση ημιτόνου στον μοναδιαίο κύκλο (πάνω) και η γραφική της παράσταση (κάτω)

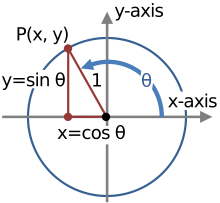
Ο μοναδιαίος κύκλος με κέντρο την αρχή στο ευκλείδειο επίπεδο ορίζεται από την εξίσωση:

$x^{2}+y^{2}=1.$

Με δεδομένη μια γωνία θ, υπάρχει ένα μοναδικό σημείο P στον μοναδιαίο κύκλο σε αριστερόστροφη γωνία θ από τον άξονα x και οι συντεταγμένες x και y του P είναι:

$x=\cos \theta \ {\text{ and }}\ y=\sin \theta .$

Συνεπώς, από την εξίσωση για τον μοναδιαίο κύκλο:

$\cos ^{2}\theta +\sin ^{2}\theta =1,$

η πυθαγόρεια ταυτότητα.

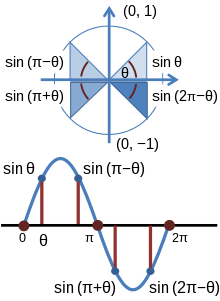
Στο σχήμα, το σημείο P έχει αρνητική συντεταγμένη x και δίνεται κατάλληλα από τη σχέση x = cos θ, η οποία είναι αρνητικός αριθμός: cos θ = -cos(π-θ). Το σημείο P έχει θετική y-συντεταγμένη, και sin θ = sin(π-θ) > 0. Καθώς το θ αυξάνεται από το μηδέν μέχρι τον πλήρη κύκλο θ = 2π, το ημίτονο και το συνημίτονο αλλάζουν πρόσημο στα διάφορα τεταρτημόρια για να διατηρήσουν τα x και y με τα σωστά πρόσημα. Το σχήμα δείχνει πώς μεταβάλλεται το πρόσημο της συνάρτησης του ημιτόνου καθώς η γωνία αλλάζει τεταρτημόριο.

Επειδή οι άξονες x και y είναι κάθετοι, αυτή η πυθαγόρεια ταυτότητα είναι ισοδύναμη με το πυθαγόρειο θεώρημα για τρίγωνα με υποτείνουσα μήκους 1 (το οποίο με τη σειρά του είναι ισοδύναμο με το πλήρες πυθαγόρειο θεώρημα εφαρμόζοντας το επιχείρημα των όμοιων τριγώνων). Βλ. κύκλος της μονάδας για μια σύντομη εξήγηση.

Απόδειξη με χρήση δυναμοσειρών

Οι τριγωνομετρικές συναρτήσεις μπορούν επίσης να οριστούν χρησιμοποιώντας δυναμοσειρές, δηλαδή (για x μια γωνία που μετριέται σε ακτίνια):

${\begin{aligned}\sin x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}x^{2n+1},\\\cos x&=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}x^{2n}.\end{aligned}}$

Χρησιμοποιώντας τον τύπο πολλαπλασιασμού για δυναμοσειρές στο Πολλαπλασιασμός και διαίρεση δυναμοσειρών (κατάλληλα τροποποιημένος ώστε να ληφθεί υπόψη η μορφή της σειράς εδώ) έχουμε

${\begin{aligned}\sin ^{2}x&=\sum _{i=0}^{\infty }\sum _{j=0}^{\infty }{\frac {(-1)^{i}}{(2i+1)!}}{\frac {(-1)^{j}}{(2j+1)!}}x^{(2i+1)+(2j+1)}\\&=\sum _{n=1}^{\infty }\left(\sum _{i=0}^{n-1}{\frac {(-1)^{n-1}}{(2i+1)!(2(n-i-1)+1)!}}\right)x^{2n}\\&=\sum _{n=1}^{\infty }\left(\sum _{i=0}^{n-1}{2n \choose 2i+1}\right){\frac {(-1)^{n-1}}{(2n)!}}x^{2n},\\\cos ^{2}x&=\sum _{i=0}^{\infty }\sum _{j=0}^{\infty }{\frac {(-1)^{i}}{(2i)!}}{\frac {(-1)^{j}}{(2j)!}}x^{(2i)+(2j)}\\&=\sum _{n=0}^{\infty }\left(\sum _{i=0}^{n}{\frac {(-1)^{n}}{(2i)!(2(n-i))!}}\right)x^{2n}\\&=\sum _{n=0}^{\infty }\left(\sum _{i=0}^{n}{2n \choose 2i}\right){\frac {(-1)^{n}}{(2n)!}}x^{2n}.\end{aligned}}$

Στην έκφραση για το sin², το n πρέπει να είναι τουλάχιστον 1, ενώ στην έκφραση για το cos2, ο σταθερός όρος είναι ίσος με 1. Οι υπόλοιποι όροι του αθροίσματός τους είναι (με αφαίρεση των κοινών παραγόντων)

$\sum _{i=0}^{n}{2n \choose 2i}-\sum _{i=0}^{n-1}{2n \choose 2i+1}=\sum _{j=0}^{2n}(-1)^{j}{2n \choose j}=(1-1)^{2n}=0$

με το διωνυμικό θεώρημα. Κατά συνέπεια,

$\sin ^{2}x+\cos ^{2}x=1,$

που είναι η πυθαγόρεια τριγωνομετρική ταυτότητα.

Όταν οι τριγωνομετρικές συναρτήσεις ορίζονται με αυτόν τον τρόπο, η ταυτότητα σε συνδυασμό με το Πυθαγόρειο θεώρημα δείχνει ότι αυτές οι δυναμοσειρές παραμετροποιούν τον μοναδιαίο κύκλο, τον οποίο χρησιμοποιήσαμε στην προηγούμενη ενότητα. Αυτός ο ορισμός κατασκευάζει τις συναρτήσεις ημιτόνου και συνημιτόνου με αυστηρό τρόπο και αποδεικνύει ότι είναι διαφορίσιμες, έτσι ώστε στην πραγματικότητα να υποκαθιστά τις δύο προηγούμενες.

Απόδειξη χρησιμοποιώντας τη διαφορική εξίσωση

Το ημίτονο και το συνημίτονο μπορούν να οριστούν ως οι δύο λύσεις της διαφορικής εξίσωσης:

$y''+y=0$

ικανοποιώντας αντίστοιχα y(0) = 0, y′(0) = 1 και y(0) = 1, y′(0) = 0. Από τη θεωρία των συνήθων διαφορικών εξισώσεων προκύπτει ότι η πρώτη λύση, το ημίτονο, έχει ως παράγωγο τη δεύτερη, το συνημίτονο, και από αυτό προκύπτει ότι η παράγωγος του συνημιτόνου είναι το αρνητικό του ημιτόνου. Η ταυτότητα είναι ισοδύναμη με τον ισχυρισμό ότι η συνάρτηση

$z=\sin ^{2}x+\cos ^{2}x$

είναι σταθερή και ίση με 1. Η διαφοροποίηση με τον κανόνα της αλυσίδας δίνει

${\frac {d}{dx}}z=2\sin x\cos x+2\cos x(-\sin x)=0,$

οπότε το z είναι σταθερό. Ένας υπολογισμός επιβεβαιώνει ότι z(0) = 1, και το z είναι σταθερά, οπότε z = 1 για όλα τα x, οπότε η πυθαγόρεια ταυτότητα είναι δεδομένη.

Μια παρόμοια απόδειξη μπορεί να ολοκληρωθεί χρησιμοποιώντας δυναμοσειρές όπως παραπάνω για να διαπιστωθεί ότι το ημίτονο έχει ως παράγωγο το συνημίτονο και το συνημίτονο έχει ως παράγωγο το αρνητικό ημίτονο. Στην πραγματικότητα, οι ορισμοί μέσω της συνήθους διαφορικής εξίσωσης και μέσω των δυναμοσειρών οδηγούν σε παρόμοιες παραγώγους των περισσότερων ταυτοτήτων.

Αυτή η απόδειξη της ταυτότητας δεν έχει άμεση σχέση με την απόδειξη του Πυθαγόρειου θεωρήματος του Ευκλείδη.

Απόδειξη με χρήση του τύπου του Όιλερ

Χρησιμοποιώντας τον τύπο του Όιλερ $e^{i\theta }=\cos \theta +i\sin \theta$ και την παραγοντοποίηση $\cos ^{2}\theta +\sin ^{2}\theta$ ως μιγαδική διαφορά δύο τετραγώνων,

${\begin{aligned}1&=e^{i\theta }e^{-i\theta }\\[3mu]&=(\cos \theta +i\sin \theta )(\cos \theta -i\sin \theta )\\[3mu]&=\cos ^{2}\theta +\sin ^{2}\theta .\end{aligned}}$

Δημοσιεύσεις

• Dembowski, Peter (1968), Finite geometries, Ergebnisse der Mathematik und ihrer Grenzgebiete, 44, Berlin: Springer, ISBN 3-540-61786-8, https://archive.org/details/finitegeometries0000demb 
• Euclid (1956). The Thirteen Books of Euclid's Elements, Translated from the Text of Heiberg, with Introduction and Commentary. 1 (Books I and II). Μτφρ. Heath, Thomas L. (Reprint of 2nd (1925) έκδοση). Dover.  On-line text at archive.org
• Bourke, Paul (Ιουλίου 1997). «Calculating the area and centroid of a polygon». 
• Abramowitz, Milton; Stegun, Irene A. (1970), Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover Publications, Ninth printing 
• Adlaj, Semjon (2012), «An Eloquent Formula for the Perimeter of an Ellipse», American Mathematical Society 59 (8): 1097, https://www.ams.org/notices/201208/rtx120801094p.pdf 
• Axler, Sheldon (2012), Algebra and Trigonometry, John Wiley & Sons, ISBN 978-0470-58579-5, https://books.google.com/books?id=B5RxDwAAQBAJ 
• Bourchtein, Ludmila; Bourchtein, Andrei (2022), Theory of Infinite Sequences and Series, Springer, doi:10.1007/978-3-030-79431-6, ISBN 978-3-030-79431-6, https://books.google.com/books?id=nGxOEAAAQBAJ 
• Boyer, Carl B. (2004), History of Analytic Geometry, Dover, ISBN 978-0-486-43832-0, https://books.google.com/books?id=2T4i5fXZbOYC 
• Oakley, C. O., Ph.D. (1944), An Outline of the Calculus, New York: Barnes & Noble 
• Protter, Murray H.; Morrey, Charles B. Jr. (1970), College Calculus with Analytic Geometry (2nd έκδοση), Reading: Addison-Wesley 

Δείτε επίσης

• Πραγματικό προβολικό επίπεδο
• Στοιχεία του Ευκλείδη
• Ευκλείδειος χώρος
• Καρτεσιανό σύστημα συντεταγμένων
• Μιγαδικός αριθμός
• τοπολογικος ισομορφισμός
• Παραβολή (γεωμετρία)
• Προβολή (γραμμική άλγεβρα)
• Θεώρημα εξαγώνου του Πάππου
• Ορθογώνιο τρίγωνο
• Τετραγωνισμός παραβολής
• Διαβήτης (όργανο)
• Διπλασιασμός του κύβου
• Προβολική γεωμετρία
• Υπερβολή (γεωμετρία)
• Μη αντιμεταθετική αλγεβρική γεωμετρία
• Κωνική τομή
• Παραλληλόγραμμο
• Πυθαγόρειο θεώρημα

Εξωτερικοί σύνδεσμοι

• English - Greek Dictionary of Pure and Applied Mathematics Εθνικό Μετσόβιο Πολυτεχνείο
• Αγγλοελληνικό Λεξικό Μαθηματικής Ορολογίας - Πανεπιστήμιο Κύπρου
• Ευκλείδεια Γεωμετρία - Πανελλήνιο Σχολικό Δίκτυο
• Euclid’s elements of geometry - The Greek text of J.L. Heiberg (1883–1885) Πανεπιστήμιο του Τέξας στο Όστιν
• Τα οπτικά του Ευκλείδη Διδακτορική Διατριβή - ΕΑΔΔ
• “Αρχιμήδους Βιβλίο Λημμάτων” – Πραγματεία του Νικολάου Λ. Κεχρή Ανοιχτή βιβλιοθήκη
• Virtual book about Archimedes Chris Rorres - Drexel University
• A History of Greek Mathematics, Τόμος 1
• A History of Greek Mathematics: Τόμος 2
• Advanced Euclidean Geometry
• Methods for Euclidean Geometry.
• Standards Driven Math: Pre-Calculus, Trigonometry, Math Analysis, Linear Algebra, Pythagorean trigonometric identity..page 17
• Barron's Math 360: A Complete Study Guide to Pre-Calculus with Online Practice.. Pythagorean trigonometric identity... page 298
• Pythagorean trigonometric identity ..Pythagorean trigonometric identity.
• Encyclopedia of Mathematics Education ...Pythagorean trigonometric identity..page 783 .
• Mathematics ...Pythagorean trigonometric identity..... page 53...
• Concise Dictionary of Mathematics ...Pythagorean trigonometric identity...page 281
• Unipotent and Nilpotent Classes in Simple Algebraic Groups and Lie Algebras..

Πηγές

• Bell, John L. (1999). The Art of the Intelligible: An Elementary Survey of Mathematics in its Conceptual Development. Kluwer. ISBN 0-7923-5972-0. 
• Euclid (1956). The Thirteen Books of Euclid's Elements, Translated from the Text of Heiberg, with Introduction and Commentary. 1 (Books I and II). Μτφρ. Heath, Thomas L. (Reprint of 2nd (1925) έκδοση). Dover.  On-line text at archive.org
• Heath, Sir Thomas (1921). «The 'Theorem of Pythagoras'». A History of Greek Mathematics (2 Vols.) (Dover Publications, Inc. (1981) έκδοση). Clarendon Press, Oxford. σελίδες 144 ff. ISBN 0-486-24073-8.