Βασικός αναπαραγωγικός αριθμός

Τιμές R₀ για πολύ γνωστές μολυσματικές ασθένειες

Ασθένεια	Μετάδοση	R0
Ιλαρά	Αερόλυμα	12–18
Ανεμοβλογιά (ανεμευλογιά)	Αερόλυμα	10–12
Παρωτίτιδα	Αναπνευστικά σταγονίδια	10–12
Πολιομυελίτιδα	Διαδρομή κοπράνων-στόματος	5–7
Ερυθρά	Αναπνευστικά σταγονίδια	5–7
Κοκκύτης	Αναπνευστικά σταγονίδια	5,5
Ευλογιά	Αναπνευστικά σταγονίδια	3,5–6
Ασθένεια κορονοϊού 2019	Αναπνευστικά σταγονίδια	1,4–5,7
HIV / AIDS	Σωματικά υγρά	2–5
SARS	Αναπνευστικά σταγονίδια	3,1–4,2
Κοινό κρυολόγημα	Αναπνευστικά σταγονίδια	2–3
Διφθερίτιδα	Σάλιο	1,7–4,3
Γρίπη (στέλεχος της πανδημίας του 1918)	Αναπνευστικά σταγονίδια	1,4–2,8
Έμπολα (έξαρση του Έμπολα 2014)	Σωματικά υγρά	1,5–1,9
Γρίπη (στέλεχος πανδημίας 2009)	Αναπνευστικά σταγονίδια	1,4–1,6
Γρίπη (εποχιακά στελέχη)	Αναπνευστικά σταγονίδια	0,9–2,1
MERS	Αναπνευστικά σταγονίδια	0,3–0,8

Ένα βίντεο που συζητάει τον βασικό αναπαραγωγικό αριθμό (σε περίπου 4 λ.) και την θνητότητα στο πλαίσιο της πανδημίας κορονοϊού 2019.

Στην επιδημιολογία, ο βασικός αναπαραγωγικός αριθμός (μερικές φορές ονομάζεται βασικός αναπαραγωγικός λόγος ή λανθασμένα βασικός αναπαραγωγικός ρυθμός) μιας λοίμωξης υποδηλώνεται με R₀ και μπορεί να θεωρηθεί ως ο αναμενόμενος αριθμός κρουσμάτων που προκύπτουν άμεσα από ένα κρούσμα σε έναν πληθυσμό όπου όλα τα άτομα είναι επιρρεπή στην μόλυνση. Ο ορισμός περιγράφει την κατάσταση όπου κανένα άλλο άτομο δεν έχει μολυνθεί ή αποκτήσει ανοσία (φυσική ή μέσω εμβολιασμού). Ορισμένοι ορισμοί, όπως αυτός του Αυστραλιανού Υπουργείου Υγείας, προσθέτουν την απουσία «οποιασδήποτε σκόπιμης παρέμβασης στη μετάδοση νόσων». Ο βασικός αναπαραγωγικός αριθμός δεν πρέπει να συγχέεται με τον αποτελεσματικό αναπαραγωγικό αριθμό R, που είναι ο αριθμός των κρουσμάτων που προκύπτουν στην τρέχουσα κατάσταση ενός πληθυσμού, ο οποίος δεν είναι απαραίτητο να μην έχει μολυνθεί. Εξ ορισμού, το R₀ δεν μπορεί να τροποποιηθεί μέσω εκστρατειών εμβολιασμού. Επίσης, είναι σημαντικό να σημειωθεί ότι το R₀ είναι ένας αριθμός χωρίς μονάδες μέτρησης και όχι ρυθμός, ο οποίος θα έχει μονάδες χρόνος^-1 ή άλλες μονάδες χρόνου όπως διπλασιασμός του χρόνου.

Το R₀ δεν είναι μια βιολογική σταθερά για ένα παθογόνο καθώς επηρεάζεται επίσης από άλλους παράγοντες, όπως οι περιβαλλοντικές συνθήκες και η συμπεριφορά του μολυσμένου πληθυσμού. Επιπλέον, οι τιμές του R₀ εκτιμώνται συνήθως από μαθηματικά μοντέλα και οι εκτιμώμενες τιμές εξαρτώνται από το μοντέλο που χρησιμοποιείται και τις τιμές άλλων παραμέτρων. Έτσι, οι τιμές που δίνονται στη βιβλιογραφία έχουν νόημα μόνο στο δεδομένο πλαίσιο και συνιστάται να μην χρησιμοποιούνται ξεπερασμένες τιμές ή να συγκρίνονται τιμές που βασίστηκαν σε διαφορετικά μοντέλα. Το R₀ δεν δίνει από μόνο του εκτίμηση του πόσο γρήγορα εξαπλώνεται μια λοίμωξη στον πληθυσμό.

Οι πιο σημαντικές χρήσεις του R₀ είναι ο προσδιορισμός της δυνατότητας μιας αναδυόμενης μολυσματικής ασθένειας να εξαπλωθεί σε έναν πληθυσμό και ο προσδιορισμός του ποσοστού του πληθυσμού που πρέπει να ανοσοποιηθεί μέσω εμβολιασμού για την εξάλειψη μιας ασθένειας. Στα συνηθισμένα μοντέλα λοίμωξης, όταν το R₀ > 1 η λοίμωξη θα είναι σε θέση να αρχίσει να εξαπλώνεται σε έναν πληθυσμό, αλλά όχι εάν το R₀ <1. Γενικά, όσο μεγαλύτερη είναι η τιμή του R₀, τόσο πιο δύσκολο είναι να ελέγχεται η επιδημία. Για απλά μοντέλα, το ποσοστό του πληθυσμού που πρέπει να ανοσοποιηθεί (που σημαίνει ότι δεν είναι επιρρεπές σε λοίμωξη) για να αποφευχθεί η παρατεταμένη εξάπλωση της λοιμώδους ασθένειας πρέπει να είναι μεγαλύτερο από 1 – 1/R₀. Από την άλλη, το ποσοστό του πληθυσμού που παραμένει επιρρεπές σε λοίμωξη κατά την ενδημική ισορροπία είναι 1/R₀.

Ο βασικός αναπαραγωγικός αριθμός επηρεάζεται από διάφορους παράγοντες, όπως η διάρκεια της μεταδοτικότητας των ασθενών που έχουν προσβληθεί, η μολυσματικότητα του παθογόνου οργανισμού και ο αριθμός των επιρρεπών ατόμων στον πληθυσμό με τους οποίους έρχονται σε επαφή τα κρούσματα.

Ιστορία

Η προέλευση της έννοιας της βασικής αναπαραγωγής μπορούν να εντοπιστεί στα έργα των Ronald Ross, Alfred Lotka και άλλων, αλλά η πρώτη σύγχρονη εφαρμογή της στην επιδημιολογία έγινε από τον George MacDonald το 1952, που δημιούργησε πληθυσμιακά μοντέλα για την εξάπλωση της ελονοσίας. Στο έργο του, όρισε τον βασικό αναπαραγωγικό ρυθμό υποδηλώνοντάς το με Z₀. Είναι παραπλανητικός ο χαρακτηρισμός του ως «ρυθμού», εφόσον ο «ρυθμός» μπορεί να παρερμηνευθεί ως αριθμός ανά μονάδα χρόνου. Προτιμάται, ο χαρακτηρισμός ως «αριθμός» ή «λόγος».

Ορισμός σε συγκεκριμένες περιπτώσεις

Ρυθμός επαφής και μολυσματική περίοδος

Το R₀ είναι ο μέσος αριθμός ατόμων που έχουν μολυνθεί από ένα άλλο άτομο. Για παράδειγμα, η έμπολα έχει R₀ ίσο με 2, οπότε κατά μέσο όρο, ένα άτομο που έχει έμπολα θα το μεταβιβάσει σε δύο άλλα άτομα.

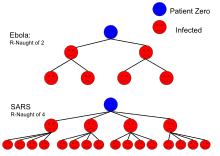
Έστω ότι τα μολυσματικά άτομα κάνουν κατά μέσο όρο $\beta$ επαφές ανά μονάδα χρόνου που οδηγούν σε μόλυνση, με μέση μολυσματική περίοδο $\tau$. Τότε ο βασικός αναπαραγωγικός αριθμός είναι:

$R_{0}=\beta \,\tau$

Αυτός ο απλός τύπος υποδηλώνει διάφορους τρόπους μείωσης του R₀ και τελικά περιορισμό της μετάδοσης της νόσου. Ο αριθμός των επαφών, $\beta$, που οδηγούν σε μόλυνση ανά μονάδα χρόνου μπορεί να μειωθεί περιορίζοντας τον αριθμό των συνολικών επαφών ανά μονάδα χρόνου (π.χ. μένοντας στο σπίτι εάν η μόλυνση απαιτεί επαφή με άλλους για να μεταδοθεί) ή μειώνοντας το ποσοστό των επαφών που προκαλούν μόλυνση (π.χ. φορώντας κάποιο είδος προστατευτικού εξοπλισμού). Είναι επίσης δυνατό να μειωθεί η μολυσματική περίοδος $\tau$ με την εύρεση και στη συνέχεια την απομόνωση, την θεραπεία ή την εξουδετέρωση (όπως συμβαίνει συχνά με τα ζώα) μολυσματικών ατόμων το συντομότερο δυνατό.

Νόσος με μεταβαλλόμενη λανθάνουσα περίοδο

Η λανθάνουσα περίοδος είναι η μεταβατική περίοδος μεταξύ της μόλυνσης και της έναρξης της μεταδοτικότητας. Σε περιπτώσεις ασθενειών με μεταβαλλόμενη λανθάνουσα περίοδο, ο βασικός αναπαραγωγικός αριθμός μπορεί να υπολογιστεί ως το άθροισμα των αναπαραγωγικών αριθμών για κάθε χρόνο μετάβασης στην ασθένεια. Ένα παράδειγμα είναι η φυματίωση (TB). Ο Blower και οι συνεργάτες του υπολόγισαν μέσα από ένα απλό μοντέλο φυματίωσης τον ακόλουθο αναπαραγωγικό αριθμό:

$R_{0}=R_{0}^{\mbox{ταχεία}}+R_{0}^{\mbox{βραδεία}}$

Στο μοντέλο τους, θεωρείται δεδομένο ότι τα μολυσμένα άτομα μπορούν να αναπτύξουν ενεργό φυματίωση είτε άμεσα (η ασθένεια αναπτύσσεται αμέσως μετά τη μόλυνση), που σημειώνεται πιο πάνω ως ταχεία φυματίωση, είτε με ενδογενή επανενεργοποίηση (η ασθένεια αναπτύσσεται χρόνια μετά την μόλυνση) που σημειώνεται πιο πάνω ως βραδεία φυματίωση.

Ετερογενείς πληθυσμοί

Σε πληθυσμούς που δεν είναι ομοιογενείς, ο ορισμός του R₀ είναι πιο σχολαστικός, καθώς πρέπει να λαμβάνει υπόψη το γεγονός ότι ένα αντιπροσωπευτικό μολυσμένο άτομο μπορεί να μην είναι αντιπροσωπευτικό του ευρύτερου πληθυσμού. Ως ακραίο παράδειγμα, παίρνουμε ένα πληθυσμό στον οποίο ένα μικρό ποσοστό των ατόμων αναμιγνύεται πλήρως μεταξύ τους, ενώ τα υπόλοιπα άτομα είναι όλα απομονωμένα. Μια ασθένεια μπορεί να είναι ικανή να εξαπλωθεί στο πλήρως αναμεμιγμένο τμήμα του πληθυσμού παρόλο που ένα τυχαία επιλεγμένο άτομο θα οδηγούσε σε λιγότερες από μία δευτερεύουσες περιπτώσεις. Αυτό συμβαίνει επειδή το μολυσμένο άτομο βρίσκεται στο πλήρως αναμεμιγμένο τμήμα και έτσι μπορεί να προκαλέσει επιτυχώς μολύνσεις. Γενικά, εάν τα άτομα που έχουν μολυνθεί νωρίς σε μια επιδημία είναι κατά μέσο όρο πιθανότερο ή λιγότερο πιθανό να μεταδώσουν τη μόλυνση σε σχέση με τα άτομα που έχουν μολυνθεί μεταγενέστερα κατά την επιδημία, τότε ο υπολογισμός του R₀ πρέπει να λαμβάνει υπόψη αυτή τη διαφορά. Ένας κατάλληλος ορισμός για το R₀ σε αυτήν την περίπτωση είναι «ο αναμενόμενος αριθμός δευτερογενών κρουσμάτων που προκύπτουν από ένα αντιπροσωπευτικό μολυσμένο άτομο νωρίς σε μια επιδημία».

Μέθοδοι εκτίμησης

Κατά την διάρκεια μιας επιδημίας, συνήθως ο αριθμός των διεγνωσμένων λοιμώξεων $N(t)$ στο χρονικό διάστημα $t$ είναι γνωστός. Στα πρώτα στάδια μιας επιδημίας, η εξάπλωση είναι εκθετική, με ρυθμό ανάπτυξης  

$K={\frac {d\ln(N)}{dt}}.$

Για την εκθετική εξάπλωση, το $N$ μπορεί να ερμηνευθεί ως ο σωρευτικός αριθμός των διαγνώσεων (συμπεριλαμβανομένων των ατόμων που έχουν αναρρώσει) ή ο τρέχων αριθμός διεγνωσμένων ασθενών. Ο εκθετικός ρυθμός ανάπτυξης είναι ο ίδιος για στις δύο περιπτώσεις. Για να εκτιμήσουμε το $R_{0}$, απαιτούνται παραδοχές σχετικά με την χρονική καθυστέρηση μεταξύ μόλυνσης και διάγνωσης και με τον χρόνο μεταξύ μόλυνσης και έναρξης της μολυσματικότητας.

Στην εκθετική εξάπλωση, το $K$ σχετίζεται με τον χρόνο διπλασιασμού, $T_{d}$, ως εξής

$K={\frac {\ln(2)}{T_{d}}}$ .

Απλό μοντέλο

Εάν ένα άτομο, αφού μολυνθεί, μολύνει ακριβώς $R_{0}$ νέα άτομα μετά από χρόνο που ισούται ακριβώς με $\tau$ (το σειραϊκό διάστημα), τότε ο αριθμός των μολυσματικών ατόμων με την πάροδο του χρόνου αυξάνεται σύμφωνα με την εξίσωση:

$n_{E}(t)=n_{E}(0)\,R_{0}^{t/\tau }$

ή

$log(n_{E}(t))=log(n_{E}(0))+log(R_{0})t/\tau .$

Σε αυτήν την περίπτωση,

$R_{0}=e^{K\tau }$ ή $K={\frac {\ln R_{0}}{\tau }}$ .

Για παράδειγμα, με $\tau =5~\mathrm {d}$ και $K=0,183~\mathrm {d} ^{-1}$, τότε $R_{0}=2,5$.

Αν το $R_{0}$ εξαρτάται από το χρόνο:

$log(n_{E}(t))=log(n_{E}(0))+{\frac {1}{\tau }}\int \limits _{0}^{t}log(R_{0}(t))dt$

δείχνοντας ότι ίσως είναι σημαντικό να διατηρηθεί το χρονικά-σταθμισμένο $log(R_{0})$ κάτω του 0, για να αποφευχθεί η εκθετική εξάπλωση.

Λανθάνουσα μολυσματική περίοδος, απομόνωση μετά τη διάγνωση

Σε αυτό το μοντέλο, μια μεμονωμένη λοίμωξη έχει τα ακόλουθα στάδια:

1. Έκθεση: ένα άτομο έχει μολυνθεί, αλλά δεν έχει συμπτώματα και δεν μολύνει ακόμη άλλους. Η μέση διάρκεια της εκτεθειμένης κατάστασης είναι $\tau _{E}$.
2. Λανθάνουσα μολυσματικότητα: ένα άτομο έχει μολυνθεί, δεν έχει συμπτώματα, αλλά μολύνει άλλους. Η μέση διάρκεια της λανθάνουσας μολυσματικής κατάστασης είναι $\tau _{I}$. Το άτομο μολύνει $R_{0}$ άλλα άτομα κατά τη διάρκεια αυτής της περιόδου.
3. Απομόνωση μετά τη διάγνωση: λαμβάνονται μέτρα για την πρόληψη περαιτέρω λοιμώξεων, για παράδειγμα, με την αποκλεισμό του ασθενούς από επαφές με άλλους.

Ακολουθεί είναι ένα μοντέλο SEIR όπου το R₀ μπορεί να υπολογιστεί από την ακόλουθη εξίσωση:

$R_{0}=1+K(\tau _{E}+\tau _{I})+K^{2}\tau _{E}\tau _{I}.$

Αυτή η μέθοδος εκτίμησης έχει εφαρμοστεί στην ασθένεια του κορονοϊού 2019 και στον ιό του SARS-1. Προκύπτει από την διαφορική εξίσωση για τον αριθμό των εκτεθειμένων ατόμων $n_{E}$ και τον αριθμό των λανθανόντως μολυσματικών ατόμων $n_{I}$,

${\frac {d}{dt}}{\begin{pmatrix}n_{E}\\n_{I}\end{pmatrix}}={\begin{pmatrix}-1/\tau _{E}&R_{0}/\tau _{I}\\1/\tau _{E}&-1/\tau _{I}\end{pmatrix}}{\begin{pmatrix}n_{E}\\n_{I}\end{pmatrix}}.$

Η μεγαλύτερη ιδιοτιμή του πίνακα είναι ο λογαριθμικός ρυθμός εξάπλωσης $K$, το οποίο μπορεί να λυθεί ως προς το $R_{0}$.

Στην ειδική περίπτωση όπου $\tau _{I}=0$, από αυτό το μοντέλο προκύπτει ότι $R_{0}=1+K\tau _{E}$, το οποίο διαφέρει από το προηγούμενο απλό μοντέλο ($R_{0}=\exp(K\tau _{E})$). Για παράδειγμα, με τις ίδιες τιμές $\tau =5~\mathrm {d}$ και $K=0,183~\mathrm {d} ^{-1}$, θα βρούμε $R_{0}=1,9$, αντί για $2,5$ . Αυτό οφείλεται σε μια λεπτή διαφορά στο υποκείμενο μοντέλο εξάπλωσης. Η παραπάνω εξίσωση πίνακα προϋποθέτει ότι οι νέοι μολυσμένοι ασθενείς μπορεί να αρχίσουν να μεταδίδουν την ασθένεια αμέσως μετά τη μόλυνση. Ο χρόνος $\tau _{E}$ είναι ο μέσος χρόνος. Αυτή η διαφορά δείχνει ότι η εκτιμώμενη τιμή του αναπαραγωγικού αριθμού $R_{0}$ εξαρτάται από το υποκείμενο μαθηματικό μοντέλο. Εάν ο αναπαραγωγικός αριθμός εκτιμάται βάσει ενός συγκεκριμένου μοντέλου, αυτή η τιμή μπορεί να συγκριθεί μόνο με μελλοντικές τιμές που προκύπτουν από το ίδιο μοντέλο.

Περιορισμοί του R₀

Όταν το R₀ υπολογίζεται από μαθηματικά μοντέλα, ιδιαίτερα από συνήθεις διαφορικές εξισώσεις, παρόλο που διατυπώνεται ο ισχυρισμός ότι έχει υπολογιστεί το R₀, στην πραγματικότητα, έχει υπολογιστεί απλά ένας ουδός, όχι ο μέσος αριθμός δευτερογενών λοιμώξεων. Υπάρχουν πολλές μέθοδοι που χρησιμοποιούνται για την εξαγωγή ενός τέτοιου ουδού από ένα μαθηματικό μοντέλο, αλλά λίγες από αυτές δίνουν πάντα την πραγματική τιμή του R₀. Αυτό είναι ιδιαίτερα προβληματικό εάν υπάρχουν ενδιάμεσοι διαβιβαστές μεταξύ ξενιστών, όπως συμβαίνει στην ελονοσία.

Ο ουδός προσδιορίζει εάν μια ασθένεια θα υποχωρήσει (εάν R₀ < 1) ή θα εξελιχθεί σε επιδημία (εάν R₀ > 1), αλλά γενικά δεν μπορεί να γίνει σύγκριση διαφόρων ασθενειών. Επομένως, οι τιμές από τον πίνακα που δίνεται στην αρχή του λήμματος πρέπει να χρησιμοποιούνται με προσοχή, ειδικά εάν οι τιμές υπολογίστηκαν από μαθηματικά μοντέλα.

Οι χρησιμοποιούμενες μέθοδοι αξιοποιούν την συνάρτηση επιβίωσης, την αναδιάταξη της μεγαλύτερης ιδιοτιμής του πίνακα Τζακόμπι, την μέθοδο επόμενης γενιάς, τον υπολογισμό τού εγγενούς ρυθμού ανάπτυξης, την ύπαρξη ενδημικής ισορροπίας, τον αριθμό των επιρρεπών ατόμων κατά την ενδημική ισορροπία, την μέση ηλικία μόλυνσης και την εξίσωση τελικού μεγέθους. Λίγες από αυτές τις μεθόδους συμφωνούν μεταξύ τους, ακόμη και όταν ξεκινούν με το ίδιο σύστημα διαφορικών εξισώσεων. Ακόμη λιγότερες υπολογίζουν στην πραγματικότητα τον μέσο αριθμό δευτερογενών μολύνσεων. Δεδομένου ότι το R₀ σπάνια παρατηρείται στον πραγματικό κόσμο και συνήθως υπολογίζεται μέσω μαθηματικού μοντέλου, αυτό περιορίζει σοβαρά τη χρησιμότητά του.

Στη λαϊκή κουλτούρα

Στην ταινία Contagion του 2011, μια φανταστική ταινία αγωνίας σχετικά με μια ιατρική καταστροφή, παρουσιάζονται οι υπολογισμοί ενός μπλόγκερ για το R₀ που αντικατοπτρίζουν την εξέλιξη μιας θανατηφόρας ιογενούς λοίμωξης από μεμονωμένα κρούσματα σε πανδημία. Οι μέθοδοι που απεικονίστηκαν ήταν ελαττωματικές.

Σημειώσεις

• Τα διαμεριστικά επιδημιολογικά μοντέλα περιγράφουν τη δυναμική της νόσου με την πάροδο του χρόνου σε έναν πληθυσμό επιρρεπών (S), μολυσματικών (I) και αναρρωσάντων (R) ατόμων χρησιμοποιώντας το μοντέλο SIR. Σημειώστε ότι στο μοντέλο SIR, τα R(0) και R₀ είναι διαφορετικές ποσότητες - το πρώτο περιγράφει τον αριθμό που ανακτήθηκε σε t = 0 ενώ το δεύτερο περιγράφει την αναλογία μεταξύ της συχνότητας των επαφών και της συχνότητας ανάρρωσης.
• Σύμφωνα με το Επαρχιακό Κέντρο Ελέγχου και Πρόληψης Νοσημάτων του Γκουανγκντόνγκ, «ο αποτελεσματικός αναπαραγωγικός αριθμός (R ή R_e) χρησιμοποιείται πιο συχνά για να περιγράψει τη μεταδοτικότητα, ο οποίος ορίζεται ως ο μέσος αριθμός δευτερογενών κρουσμάτων που προκύπτουν ανά μολυσματικό κρούσμα. Απουσία μέτρων ελέγχου, R = R₀χ, όπου το χ είναι το ποσοστό του επιρρεπούς πληθυσμού.» Για παράδειγμα, σύμφωνα με μια προκαταρκτική εκτίμηση, ο αποτελεσματικός αναπαραγωγικός αριθμός για τον κορονοϊό της Ουχάν βρέθηκε να είναι 2,9, ενώ για τον ιό του SARS-1 ήταν 1,77.
• Ο αποτελεσματικός αναπαραγωγικός αριθμός, R_e, μπορεί να μειωθεί με μέτρα παρέμβασης όπως η κοινωνική απομάκρυνση, ενώ το R₀ παραμένει ανεπηρέαστο, καθώς είναι ένα μέτρο του ρυθμού μόλυνσης όταν δεν υπάρχουν παρεμβάσεις.

Περαιτέρω ανάγνωση

• Heesterbeek, J.A.P. (2002). «A brief history of R₀ and a recipe for its calculation». Acta Biotheoretica 50 (3): 189–204. doi:10.1023/A:1016599411804. PMID 12211331. https://www.researchgate.net/publication/216638420. 
• Heffernan, J.M.; Smith, R.J.; Wahl, L.M. (October 2005). «Perspectives on the basic reproductive ratio». Journal of the Royal Society Interface 2 (4): 281–293. doi:10.1098/rsif.2005.0042. PMID 16849186. 
• Jones, James Holland (1 Μαΐου 2007). «Notes on R₀» (PDF). Ανακτήθηκε στις 6 Νοεμβρίου 2018. 
• Van Den Driessche, P.· Watmough, James (2008). «Further Notes on the Basic Reproduction Number». Mathematical Epidemiology. Lecture Notes in Mathematics. 1945. σελίδες 159–178. ISBN 978-3-540-78910-9.