Εικασία του Ανρίκα

(a) Η συνάρτηση

A_{n}

για τους πρώτους 100 πρώτους αριθμούς.

(b) Η συνάρτηση

A_{n}

για τους πρώτους 200 πρώτους αριθμούς.

(c) Η συνάρτηση

A_{n}

για τους πρώτους 500 πρώτους αριθμούς.

Γραφική απόδειξη της εικασίας του Αντρίκα για τους πρώτους (α)100, (β)200 και (γ)500 πρώτους αριθμούς. Εικάζεται ότι η συνάρτηση

A_{n}

είναι πάντα μικρότερη από 1.

Η εικασία του Αντρίκα^[1]^[2] (που πήρε το όνομά της από τον Ρουμάνο μαθηματικό Ντορίν Αντρίκα) είναι μια εικασία σχετικά με τα κενά μεταξύ των πρώτων αριθμών.^[3]^[4]

Η εικασία δηλώνει ότι η ανισότητα

{\sqrt {p_{n+1}}}-{\sqrt {p_{n}}}<1

ισχύει για όλα τα $n$ , όπου $p_{n}$ είναι ο n πρώτος αριθμός. Αν $g_{n}=p_{n+1}-p_{n}$ συμβολίζει το n th κενά μεταξύ πρώτων, τότε η εικασία του Αντρίκα μπορεί επίσης να επαναδιατυπωθεί ως εξής

g_{n}<2{\sqrt {p_{n}}}+1.

Εμπειρικά στοιχεία

Ο Ιμράν Γκόρι χρησιμοποίησε δεδομένα σχετικά με τα μεγαλύτερα κενά πρώτων αριθμών για να επιβεβαιώσει την εικασία για $n$ μέχρι 1.3002 × 10¹⁶.^[5] Χρησιμοποιώντας έναν πίνακα μέγιστων κενών και την παραπάνω ανισότητα κενών, η τιμή επιβεβαίωσης μπορεί να επεκταθεί εξαντλητικά μέχρι 4 × 10¹⁸. Χρησιμοποιώντας έναν πίνακα μέγιστων κενών και την παραπάνω ανισότητα κενών, η τιμή επιβεβαίωσης μπορεί να επεκταθεί εξαντλητικά μέχρι 4 × 10¹⁸.

Η διακριτή συνάρτηση $A_{n}={\sqrt {p_{n+1}}}-{\sqrt {p_{n}}}$ απεικονίζεται στα διπλανά σχήματα. Τα υψηλά σημεία για το $A_{n}$ εμφανίζονται για n = 1, 2, και 4, με A₄ ≈ 0.670873..., χωρίς μεγαλύτερη τιμή μεταξύ των πρώτων 105 πρώτων αριθμών. Δεδομένου ότι η συνάρτηση Αντρίκα μειώνεται ασυμπτωτικά καθώς αυξάνεται το n, απαιτείται ένα κενό πρώτων αριθμών ολοένα και μεγαλύτερου μεγέθους για να γίνει η διαφορά μεγάλη καθώς το n γίνεται μεγάλο. Επομένως, φαίνεται πολύ πιθανό η εικασία να είναι αληθής, αν και αυτό δεν έχει ακόμη αποδειχθεί.

Γενικεύσεις

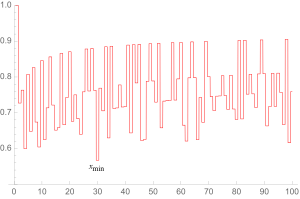
Ως γενίκευση της εικασίας του Αντρίκα, θεωρήθηκε η ακόλουθη εξίσωση:

p_{n+1}^{x}-p_{n}^{x}=1,

όπου $p_{n}$ είναι ο nth πρώτος και x μπορεί να είναι οποιοσδήποτε θετικός αριθμός.

Η μεγαλύτερη δυνατή λύση για το x φαίνεται εύκολα ότι εμφανίζεται για n=1, όταν x_max = 1. Η μικρότερη λύση για το x εικάζεται ότι είναι x_min ≈ 0.567148... ((ακολουθία A038458 στην OEIS)), η οποία εμφανίζεται για n = 30.

Η εικασία αυτή έχει επίσης διατυπωθεί ως ανισότητα, η γενικευμένη εικασία Ανδρίκα:

p_{n+1}^{x}-p_{n}^{x}<1

for

x<x_{\min }.

Εξωτερικοί σύνδεσμοι

Δείτε επίσης

Βιβλιογραφία

Andreescu, Titu· Andrica, Dorin (12 Ιουνίου 2009). Number Theory: Structures, Examples, and Problems. Springer Science & Business Media. ISBN 978-0-8176-4645-5.
Pickover, Clifford A. (27 Σεπτεμβρίου 2011). The Math Book: From Pythagoras to the 57th Dimension, 250 Milestones in the History of Mathematics. Union Square & Co. ISBN 978-1-4027-9749-1.
Rassias, Michael Th (16 Νοεμβρίου 2010). Problem-Solving and Selected Topics in Number Theory: In the Spirit of the Mathematical Olympiads. Springer Science & Business Media. ISBN 978-1-4419-0495-9.
Elwes, Richard (27 Σεπτεμβρίου 2012). How to Solve the Da Vinci Code: And 34 Other Really Interesting Uses of Mathematics. Quercus. ISBN 978-0-85738-462-1.
Ashbacher, Charles. Smarandache Function Journal, vol. 12/2001: An International Book Series in Information Science and Engineering. Infinite Study.
Smarandache, Florentin (1 Δεκεμβρίου 1999). Definitions, Solved and Unsolved Problems, Conjectures, and Theorems in Number Theory and Geometry. Infinite Study. ISBN 978-1-879585-74-4.
Agarwal, Ravi P. Mathematics Before and After Pythagoras. Springer Nature. ISBN 978-3-031-74224-8.
Mao, Linfan. International Journal of Mathematical Combinatorics, Volume 4, 2014. Infinite Study.
Guy, Richard (11 Νοεμβρίου 2013). Unsolved Problems in Number Theory. Springer Science & Business Media. ISBN 978-1-4899-3585-4.
Guàrdia, Jordi· Minculete, Nicuşor (2024). New Frontiers in Number Theory and Applications. Springer Nature. ISBN 978-3-031-51959-8.

Παραπομπές

↑ SMARANDACHE, FLORENTIN. Conjectures Which Generalize Andrica's Conjecture. Infinite Study.
↑ Weisstein, Eric W. (12 Δεκεμβρίου 2002). CRC Concise Encyclopedia of Mathematics. CRC Press. ISBN 978-1-4200-3522-3.
↑ Andrica, D. (1986). «Note on a conjecture in prime number theory». Studia Univ. Babes–Bolyai Math. 31 (4): 44–48. ISSN 0252-1938.
Zbl 0623.10030
.
↑ Internet Archive, Tom M. (1986). Introduction to analytic number theory. New York : Springer-Verlag. ISBN 978-0-387-90163-3.
↑ Wells, David (18 Μαΐου 2005). Prime Numbers: The Most Mysterious Figures in Math. Hoboken (N.J.): Wiley. σελ. 13. ISBN 978-0-471-46234-7.

Deza, Elena (6 Αυγούστου 2021). Mersenne Numbers And Fermat Numbers. World Scientific. ISBN 978-981-12-3033-2.
Sándor, J. (2002). Geometric Theorems, Diophantine Equations, and Arithmetic Functions. Infinite Study. ISBN 978-1-931233-51-4.
Andreescu, Titu· Andrica, Dorin (5 Απριλίου 2007). 104 Number Theory Problems: From the Training of the USA IMO Team. Springer Science & Business Media. ISBN 978-0-8176-4561-8.
Stewart, Ian (2 Οκτωβρίου 2014). Professor Stewart's Casebook of Mathematical Mysteries. Profile. ISBN 978-1-84765-432-8.
Igarashi, Yoshihide· Altman, Tom (27 Μαΐου 2014). Computing: A Historical and Technical Perspective. CRC Press. ISBN 978-1-4822-2741-3.

Πηγές

Apostol, Thomas M. (1976), Introduction to Analytic Number Theory, New York: Springer, ISBN 0-387-90163-9, https://archive.org/details/introductiontoan00apos_0
Conway, John Horton; Guy, Richard K. (1996), The Book of Numbers, New York: Copernicus, ISBN 978-0-387-97993-9
Crandall, Richard; Pomerance, Carl (2005), Prime Numbers: A Computational Perspective (2nd έκδοση), Berlin, New York: Springer-Verlag, ISBN 978-0-387-25282-7
Singer, I. M.· Thorpe, J. A. (28 Μαΐου 2015). Lecture Notes on Elementary Topology and Geometry. Springer. ISBN 978-1-4615-7347-0.
Apostol, Tom M. (29 Ιουνίου 2013). Introduction to Analytic Number Theory. Springer Science & Business Media. ISBN 978-1-4757-5579-4.
Miller, P. D. (2006), Applied Asymptotic Analysis, American Mathematical Society, ISBN 9780821840788, https://books.google.com/books?id=KQvqBwAAQBAJ
Apostol, Thomas M. (1976), Introduction to Analytic Number Theory, New York: Springer, ISBN 0-387-90163-9, https://archive.org/details/introductiontoan00apos_0

[1] SMARANDACHE, FLORENTIN. Conjectures Which Generalize Andrica's Conjecture. Infinite Study.

[2] Weisstein, Eric W. (12 Δεκεμβρίου 2002). CRC Concise Encyclopedia of Mathematics. CRC Press. ISBN 978-1-4200-3522-3.

[3] Andrica, D. (1986). «Note on a conjecture in prime number theory». Studia Univ. Babes–Bolyai Math. 31 (4): 44–48. ISSN 0252-1938.
Zbl 0623.10030
.

[4] Internet Archive, Tom M. (1986). Introduction to analytic number theory. New York : Springer-Verlag. ISBN 978-0-387-90163-3.

[Wells_2005_prime_numbers-5] Wells, David (18 Μαΐου 2005). Prime Numbers: The Most Mysterious Figures in Math. Hoboken (N.J.): Wiley. σελ. 13. ISBN 978-0-471-46234-7.

[1]

[2]

[3]

[4]

[5]