Μετάβαση στο περιεχόμενο

Περί επιπέδων ισορροπιών

Από τη Βικιπαίδεια, την ελεύθερη εγκυκλοπαίδεια
Περί επιπέδων ισορροπιών
ΣυγγραφέαςΑρχιμήδης
ΤίτλοςΠερὶ ἐπιπέδων ἱσορροπιῶν
ΓλώσσαΑρχαία ελληνική γλώσσα
Ημερομηνία δημοσίευσης3ος αιώνας π.Χ.
ΜορφήΦυσική, Γεωμετρία
ΘέμαΚέντρο μάζας
Μοχλός
δεδομένα (π • σ • ε )

Το έργο Περί επιπέδων ισορροπιών είναι μια πραγματεία του Αρχιμήδη σε δύο βιβλία. Το πρώτο βιβλίο περιέχει την απόδειξη του νόμου του μοχλού και κορυφώνεται με προτάσεις για το κέντρο βάρους του τριγώνου και του τραπεζίου [1][2] Το δεύτερο βιβλίο, που περιέχει δέκα προτάσεις, εξετάζει τα κέντρα βάρους των παραβολικών τμημάτων[1].

Σύμφωνα με τον Πάππο της Αλεξάνδρειας, η εργασία του Αρχιμήδη πάνω στους μοχλούς και η κατανόηση του μηχανικού πλεονεκτήματος τον οδήγησαν να πει: «Δώστε μου ένα σημείο στήριξης και θα κινήσω τη Γη» (Δωρική φωνή Συρακουσία: Πᾷ βῶ καὶ χαριστίωνι τὰν γᾶν κινήσω πᾶσαν[3]), αν και άλλες αρχαίες μαρτυρίες δεν είναι ξεκάθαρες ως προς το περιεχόμενο της ρήσης[4][5].

Γενικά

[Επεξεργασία | επεξεργασία κώδικα]

Ο μοχλός και οι ιδιότητές του ήταν ήδη γνωστά πριν από την εποχή του Αρχιμήδη, και δεν ήταν ο πρώτος που παρείχε μια ανάλυση της σχετικής αρχής [6].Τα παλαιότερα Μηχανικά Προβλήματα, που κάποτε αποδόθηκαν στον Αριστοτέλη, αλλά πιθανότατα γράφτηκαν από έναν από τους διαδόχους του, περιέχουν μια πρόχειρη απόδειξη του νόμου του μοχλού χωρίς να χρησιμοποιούν την έννοια του κέντρου μάζας. Υπάρχει ένα άλλο σύντομο έργο που αποδίδεται στον Ευκλείδη με τίτλο Περί ισορροπίας, το οποίο επίσης περιέχει μια μαθηματική απόδειξη του νόμου, και πάλι χωρίς προσφυγή στο Κέντρο μάζας[7] .

Αντίθετα, στο έργο του Αρχιμήδη η έννοια του κέντρου μάζας παίζει καθοριστικό ρόλο [8]. Το βιβλίο Περί επιπέδων ισορροπιών Ι, το οποίο περιέχει επτά αξιώματα και δεκαπέντε προτάσεις, χρησιμοποιεί το κέντρο μάζας τόσο για τα συγκρίσιμα όσο και για τα ασυμβίβαστα μεγέθη για να δικαιολογήσει το νόμο του μοχλού, αν και ορισμένοι υποστηρίζουν ότι δεν είναι ικανοποιητικό[2]. ο Αρχιμήδης στη συνέχεια προχωρά στον εντοπισμό του κέντρου μάζας του παραλληλογράμμου και του τριγώνου, και τελειώνει το πρώτο βιβλίο με μια απόδειξη για το κέντρο μάζας του τραπεζίου.

Το Περί επιπέδων ισορροπιών ΙΙ έχει το ίδιο θέμα με το πρώτο βιβλίο, αλλά πιθανότατα γράφτηκε μετέπειτα. Περιέχει δέκα προτάσεις σχετικά με το κέντρο μάζας που αφορούν αποκλειστικά τα παραβολικά τμήματα και εξετάζει τα τμήματα αυτά αντικαθιστώντας τα με ορθογώνια ίσου εμβαδού. Η ανταλλαγή αυτή καθίσταται δυνατή χάρη στα αποτελέσματα που προέκυψαν από το τετραγωνισμό της παραβολής, μια πραγματεία που πιστεύεται ότι δημοσιεύθηκε μετά το πρώτο βιβλίο του Περί επιπέδων ισορροπιών [1][2].

Περιεχόμενο

[Επεξεργασία | επεξεργασία κώδικα]

Πρώτο βιβλίο

[Επεξεργασία | επεξεργασία κώδικα]

Το πρώτο μισό του πρώτου βιβλίου ασχολείται με τις ιδιότητες της ζυγαριάς και τον νόμο του μοχλού, ενώ το δεύτερο μισό επικεντρώνεται στο κέντρο μάζας των βασικών επίπεδων σχημάτων. Το επιχείρημα που επιτρέπει στον Αρχιμήδη να θεμελιώσει το νόμο του μοχλού και να εντοπίσει το κέντρο μάζας πολλών σχημάτων είναι το έκτο αξίωμα, δηλαδή, «εάν τα μεγέθη σε ορισμένες αποστάσεις βρίσκονται σε ισορροπία, άλλα (μεγέθη) ίσα με αυτά θα βρίσκονται επίσης σε ισορροπία στις ίδιες αποστάσεις.[9] Στις προτάσεις 4 και 5, ο Αρχιμήδης αποδεικνύει ότι το κέντρο μάζας οποιουδήποτε συστήματος που αποτελείται από άρτιο αριθμό ίσων βαρών, ισομερώς κατανεμημένων, θα βρίσκεται στο μέσο μεταξύ των δύο κεντρικών βαρών. Στη συνέχεια, ο Αρχιμήδης χρησιμοποιεί αυτά τα θεωρήματα για να αποδείξει το νόμο του μοχλού στην Πρόταση 6 (για τις ανάλογες περιπτώσεις) και στην Πρόταση 7

Θεώρημα

Βάρη και μοχλός σε αναλογία 4:3.

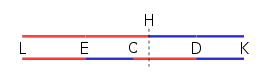
Με σύγχρονους όρους, δεδομένων δύο άνισων, αλλά συγκρίσιμων, βαρών και ενός μοχλοβραχίονα χωρισμένου σε δύο άνισα, αλλά συγκρίσιμα, τμήματα (βλέπε διπλανό σκίτσο), αν τα μεγέθη Α και Β εφαρμοστούν στα σημεία Ε και D, αντίστοιχα, το σύστημα θα βρίσκεται σε ισορροπία στο σημείο C αν τα βάρη είναι αντιστρόφως ανάλογα των μηκών:

Απόδειξη

Ας υποθέσουμε ότι οι γραμμές και τα βάρη κατασκευάζονται για να υπακούουν στον κανόνα χρησιμοποιώντας ένα κοινό μέτρο (ή μονάδα) n και σε αναλογία 4:3. Τώρα, διπλασιάζουμε το μήκος του ED διπλασιάζοντας τον μακρύτερο βραχίονα στα αριστερά, και τον κοντύτερο βραχίονα στα δεξιά.

Για να γίνει αντιληπτό, αναδιατάξτε τις γραμμές έτσι ώστε το CD να είναι δίπλα στο LE (οι δύο κόκκινες γραμμές μαζί) και αντιπαραβάλλετε τις με το πρωτότυπο (όπως παρακάτω):

Είναι σαφές ότι και οι δύο γραμμές έχουν διπλάσιο μήκος από την αρχική γραμμή ED, ότι η LH έχει το κέντρο της στο E και ότι η HK έχει το κέντρο της στο D. Σημειώστε, επιπλέον, ότι η EH (η οποία είναι ίση με την CD) μεταφέρει το κοινό μέτρο (ή μονάδα) n έναν ακριβή αριθμό φορών, όπως και η EC και, κατ' επέκτασιν, η CH. Μένει λοιπόν να αποδείξουμε ότι το Α που εφαρμόζεται στο Ε, και το Β που εφαρμόζεται στο D, θα έχουν το κέντρο βάρους τους στο C.

Επομένως, καθώς ο λόγος LH προς HK έχει διπλασιάσει τις αρχικές αποστάσεις CD και EC, ομοίως διαιρούμε τα μεγέθη A και B σε αναλογία 8:6 (ένας μετασχηματισμός που διατηρεί την αρχική τους αναλογία 4:3), και τα ευθυγραμμίζουμε έτσι ώστε οι μονάδες A (κόκκινες) να βρίσκονται στο κέντρο του E, ενώ οι μονάδες B (μπλε) στο κέντρο του D.

Τώρα, δεδομένου ότι ένας άρτιος αριθμός ίσων βαρών, σε ίσες αποστάσεις, έχουν το κέντρο μάζας τους μεταξύ των δύο μεσαίων βαρών, το Α εφαρμόζεται στην πραγματικότητα στο Ε και το Β στο D, όπως απαιτεί η πρόταση. Περαιτέρω, το συνολικό σύστημα αποτελείται από άρτιο αριθμό ίσων βαρών που είναι ισομερώς κατανεμημένα και, επομένως, ακολουθώντας τον ίδιο νόμο, το C πρέπει να είναι το κέντρο μάζας του πλήρους συστήματος. Έτσι, το σύστημα δεν έχει κλίση αλλά βρίσκεται σε ισορροπία.[1]

Δεύτερο βιβλίο

[Επεξεργασία | επεξεργασία κώδικα]

Ο κύριος στόχος του δεύτερου βιβλίου του βιβλίου Περί επιπέδων ισορροπιών είναι ο προσδιορισμός του κέντρου μάζας οποιουδήποτε τμήματος ενός παραβολικού τμήματος, όπως φαίνεται στην Πρόταση 8.

Το βιβλίο αρχίζει με μια απλούστερη απόδειξη του νόμου του μοχλού στην Πρόταση 1, κάνοντας αναφορά σε αποτελέσματα που βρέθηκαν στο Τετραγωνισμό της Παραβολής. Ο Αρχιμήδης αποδεικνύει τις επόμενες επτά προτάσεις συνδυάζοντας την έννοια του κέντρου βάρους και τις ιδιότητες της παραβολής με τα αποτελέσματα που βρέθηκαν προηγουμένως στο Περί επιπέδων ισορροπιών Ι. Συγκεκριμένα, συμπεραίνει ότι δύο παραβολές που έχουν ίσο εμβαδόν έχουν το κέντρο μάζας τους σε ίση απόσταση από κάποιο σημείο και αργότερα αντικαθιστά τα εμβαδά τους με ορθογώνια ίσου εμβαδού[1].

Οι δύο τελευταίες προτάσεις, οι προτάσεις 9 και 10, είναι μάλλον αόριστες, αλλά επικεντρώνονται στον προσδιορισμό του κέντρου μάζας ενός σχήματος που αποκόπτεται από οποιοδήποτε παραβολικό τμήμα με ένα κόλουρο κώνο [10].

Κληρονομιά

[Επεξεργασία | επεξεργασία κώδικα]

Τα μηχανολογικά έργα του Αρχιμήδη, μεταξύ των οποίων και το Περί επιπέδων ισορροπιών, ήταν γνωστά αλλά ελάχιστα διαβασμένα στην αρχαιότητα. Τόσο ο Ήρων ο Αλεξανδρεύς όσο και ο Πάππος κάνουν αναφορές στον Αρχιμήδη στο έργο τους για τη μηχανική, κυρίως στις συζητήσεις τους σχετικά με το κέντρο βάρους και το μηχανικό πλεονέκτημα. Λίγοι Ρωμαίοι συγγραφείς, όπως ο Βιτρούβιος, προφανώς είχαν επίσης κάποια γνώση του έργου του Αρχιμήδη[11][9].

Κατά τον Μεσαίωνα, ορισμένοι Άραβες συγγραφείς γνώριζαν και επέκτειναν το έργο του Αρχιμήδη σχετικά με τις ισορροπίες και το κέντρο μάζας - στη Λατινική Δύση, ωστόσο, οι ιδέες αυτές ήταν ουσιαστικά άγνωστες, εκτός από μια χούφτα περιορισμένων περιπτώσεων[12][13]. μόνο κατά την ύστερη Αναγέννηση τα αποτελέσματα που βρέθηκαν στο Περί επιπέδων ισορροπιών άρχισαν να διαδίδονται ευρέως. Ειδικά η μαθηματική προσέγγιση του Αρχιμήδη στη φυσική έγινε πρότυπο για μεταγενέστερους επιστήμονες όπως ο Γκουιντομπάλντο ντελ Μόντε, ο Μπερναρντίνο Μπάλντι, ο Σιμόν Στέβιν και ο Γαλιλαίος Γαλιλέι[14][15].

Η έννοια του κέντρου μάζας έφτασε σε υψηλό επίπεδο εξειδίκευσης στο πρώτο μισό του 17ου αιώνα, ιδιαίτερα στα έργα του Ευαγγελίστα Τοριτσέλι και του Κρίστιαν Χόιγκενς, και έπαιξε καθοριστικό ρόλο στην ανάπτυξη της ορθολογικής μηχανικής[16][17].

Κριτική

[Επεξεργασία | επεξεργασία κώδικα]

Πολλοί ερευνητές υπογράμμισαν ασυνέπειες στο πρώτο βιβλίο του Περί επιπέδων ισορροπιών[2][18] Ο Μπέργκρεν αμφισβητεί τη γνησιότητα σχεδόν του μισού πρώτου βιβλίου, για παράδειγμα τον περιττό χαρακτήρα των προτάσεων 1-3 και 11-12. Ωστόσο, ακολουθεί τον Ντίκστερχουις στην απόρριψη της κριτικής του Μαχ για την Πρόταση 6, η οποία πράγματι αποδεικνύει ότι «αν ένα σύστημα βαρών που αναρτώνται σε μια δοκό ισορροπίας βρίσκεται σε ισορροπία όταν στηρίζεται σε ένα συγκεκριμένο σημείο, τότε οποιαδήποτε ανακατανομή αυτών των βαρών, που διατηρεί το κοινό κέντρο μάζας τους, διατηρεί επίσης την ισορροπία»[2][10] .

Επιπλέον, η Πρόταση 7 του πρώτου βιβλίου εμφανίζεται ελλιπής στην τρέχουσα μορφή της, έτσι ώστε, για την ακρίβεια, ο Αρχιμήδης στο πρώτο βιβλίο καταδεικνύει το νόμο του μοχλού μόνο για συγκρίσιμα μεγέθη[1][2]. Το δεύτερο βιβλίο του Περί επιπέδων ισορροπιών δεν επηρεάζεται από αυτές τις παραλείψεις, διότι, με εξαίρεση την πρώτη πρόταση, ο μοχλός δεν εξετάζεται καθόλου.[10] Δεν υπάρχει επίσης κανένας ορισμός του κέντρου μάζας πουθενά στα σωζόμενα έργα του Αρχιμήδη, γεγονός που, σύμφωνα με ορισμένους μελετητές, καθιστά δύσκολη την παρακολούθηση (ή την αιτιολόγηση) της λογικής δομής ορισμένων επιχειρημάτων του στο Περί επιπέδων ισορροπιών[6][8].

Δημοσιεύσεις

[Επεξεργασία | επεξεργασία κώδικα]

Δείτε επίσης

[Επεξεργασία | επεξεργασία κώδικα]

Παραπομπές

[Επεξεργασία | επεξεργασία κώδικα]
  1. ↑ 1,0 1,1 1,2 1,3 1,4 1,5 Heath, T.L. (1897). «The Works of Archimedes (1897). The unabridged work in PDF form (19 MB)». Cambridge University Press. Αρχειοθετήθηκε από το πρωτότυπο στις 6 Οκτωβρίου 2007. Ανακτήθηκε στις 6 Ιανουαρίου 2013. 
  2. ↑ 2,0 2,1 2,2 2,3 2,4 2,5 Berggren, J. L. (1976). «Spurious Theorems in Archimedes' Equilibrium of Planes Book I». Archive for History of Exact Sciences 16 (2): 87–103. doi:10.1007/BF00349632. ISSN 1432-0657. 
  3. ↑ Megalē Hellēnikē enkyklopaideia. Ekdot. Organismos "Ho phoinix". 1956. 
  4. ↑ Quoted by Pappus of Alexandria in Synagoge, Book VIII, p. 1060 in ed. Hultsch
  5. ↑ Berryman, S. (2020). «How Archimedes Proposed to Move the Earth». Isis 111 (3): 562–567. doi:10.1086/710317. ISSN 0021-1753. https://www.journals.uchicago.edu/doi/abs/10.1086/710317. 
  6. ↑ 6,0 6,1 Goe, G. (1972). «Archimedes' theory of the lever and Mach's critique» (στα αγγλικά). Studies in History and Philosophy of Science Part A 2 (4): 329–345. doi:10.1016/0039-3681(72)90002-7. ISSN 0039-3681. Bibcode: 1972SHPSA...2..329G. https://dx.doi.org/10.1016/0039-3681%2872%2990002-7. 
  7. ↑ Renn, J., Damerow, P., & McLaughlin, P. (2003). Aristotle, Archimedes, Euclid, and the origin of mechanics: The perspective of historical epistemology. In J. L. Montesinos Sirera (Ed.), Symposium Arquímedes Fundación Canaria Orotava de Historia de la Ciencia (pp. 43–59). http://www.mpiwg-berlin.mpg.de/Preprints/P239.PDF.
  8. ↑ 8,0 8,1 Magnaghi, C. P.; Assis, A. K. T. (2012-05-07). «Calculation of the centre of gravity of the cone utilizing the method of Archimedes». European Journal of Physics 33 (3): 637–646. doi:10.1088/0143-0807/33/3/637. ISSN 0143-0807. Bibcode: 2012EJPh...33..637M. https://iopscience.iop.org/article/10.1088/0143-0807/33/3/637. 
  9. ↑ 9,0 9,1 Assis, A.K.T. (2010). Archimedes, the Center of Gravity, and the First Law of Mechanics (2nd έκδοση). C. Roy Keys Incorporated. ISBN 9780986492648. 
  10. ↑ 10,0 10,1 10,2 Dijksterhuis, E.J. (1987). Archimedes. Princeton University Press, Princeton. ISBN 0-691-08421-1.  Republished translation of the 1938 study of Archimedes and his works by an historian of science.
  11. ↑ Drachmann, A. G. (1968). «Archimedes and the Science of Physics» (στα αγγλικά). Centaurus 12 (1): 1–11. doi:10.1111/j.1600-0498.1968.tb00074.x. ISSN 0008-8994. Bibcode: 1968Cent...12....1D. https://onlinelibrary.wiley.com/doi/10.1111/j.1600-0498.1968.tb00074.x. 
  12. ↑ Clagett, M. (1959). «The Impact of Archimedes on Medieval Science». Isis 50 (4): 419–429. doi:10.1086/348797. ISSN 0021-1753. https://www.jstor.org/stable/226426. 
  13. ↑ Høyrup, J. (2019), Høyrup, J., επιμ., (Article I.16.) Archimedes – Knowledge and Lore from Latin Antiquity to the Outgoing European Renaissance, Cham: Springer International Publishing, σελ. 459–477, doi:10.1007/978-3-030-19258-7_17, ISBN 978-3-030-19258-7, https://doi.org/10.1007/978-3-030-19258-7_17 
  14. ↑ Palmieri, P. (2008). «Breaking the circle: the emergence of Archimedean mechanics in the late Renaissance» (στα αγγλικά). Archive for History of Exact Sciences 62 (3): 301–346. doi:10.1007/s00407-007-0012-8. ISSN 1432-0657. https://doi.org/10.1007/s00407-007-0012-8. 
  15. ↑ Meli, D. (2010). «The axiomatic tradition in seventeenth-century mechanics». Discourse on a New Method: Reinvigorating the Marriage of History and Philosophy of Science (στα Αγγλικά). Open Court. σελίδες 23–41. ISBN 978-0-8126-9662-2. 
  16. ↑ Pisano, R.; Bussotti, P.; Bussotti, Paolo; Bussotti, Paolo (2014). «Notes on mechanics and mathematics in Torricelli as physics mathematics relationships in the history of science.». Problems of Education in the 21st Century 61: 88–97. doi:10.33225/pec/14.61.88. ISSN 1822-7864. http://www.scientiasocialis.lt/pec/node/922. 
  17. ↑ Van Dyck, M. (2020), Mechanical philosophy : science of mechanics, Springer, σελ. 1–11, ISBN 978-3-319-20791-9, http://hdl.handle.net/1854/LU-8678741 
  18. ↑ Mach, E. (1907). The science of Mechanics a Critical and Historical Account of its Development. Open Court, Chicago.  Republished translation of the 1883 original by Thomas J. McCormack. Ed. 3, rev.

Εξωτερικοί σύνδεσμοι

[Επεξεργασία | επεξεργασία κώδικα]

Πηγές

[Επεξεργασία | επεξεργασία κώδικα]
Ανακτήθηκε από "https://el.wikipedia.org/w/index.php?title=Περί_επιπέδων_ισορροπιών&oldid=10798617"